Kvant. Веревочка
Гельфгат И. Сколько веревочке ни виться //Квант. — 1993. — № 1. — С. 55-56.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Рассмотрим обычную, на первый взгляд, задачу. С небольшими вариациями она не раз предлагалась на экзаменах и физических олимпиадах. Вот ее условие:
Шнур длиной L лежит на гладком горизонтальном столе, причем его небольшая часть свешивается с края стока. Лежащий на столе конец шнура сначала удерживают, а затем отпускают. Определите скорость шнура υ и его ускорение а к тому моменту, когда длина свешивающейся части будет равна х.
Приведем обычно встречающееся решение этой задачи. Если масса шнура m, то масса его свешивающейся части равна \(~m \frac xL\). Центр тяжести этой части шнура находится на \(~\frac x2\) ниже поверхности стола, значит, при соскальзывании потенциальная энергия шнура уменьшилась на \(~mg \frac xL \frac x2\). Согласно закону сохранения энергии, эту величину можно приравнять к кинетической энергии шнура \(~\frac{m \upsilon^2}{2}\). Тогда для скорости шнура получаем
Ускорение всему шнуру придает сила тяжести его свешивающейся части, поэтому из второго закона Ньютона \(~ma = mg \frac xL\) следует
Итак, задача решена? Полученные выражения имеют правильную размерность и приводят к вполне разумным результатам в предельных случаях х → 0 и x → L. Значит, говорить больше не о чем?
Не судите опрометчиво. Попробуем ответить на один провокационный вопрос: как меняется при движении шнура горизонтальная проекция px его импульса[1]? Поскольку горизонтальную скорость имеет только находящаяся на столе часть шнура массой \(~m \frac{L - x}{L} \), получаем
Значит, при увеличении х импульс px растет только пока \(~x < \frac L2\). Дальше импульс убывает и при х = L обращается в ноль (шнур падает теперь вертикально).
Но ведь для уменьшения импульса необходима внешняя сила, тормозящая соскальзывание. Где же она? Не ищите — в отсутствие трения такой силы не найти. И потому неясно, за счет чего гасится горизонтальная проекция скорости шнура.
Правильный ответ такой: никакого уменьшения импульса не происходит. Мы предполагали, что каждый элемент шнура, проходя край стола, резко меняет горизонтальное движение на вертикальное, именно при этом и теряется горизонтальный импульс. Но может быть, реальное движение сложнее? Возможно, набрав достаточно большую скорость, элементы шнура сохраняют ее (по крайней мере, частично) и после соскальзывания со стола и тогда никакого противоречия не возникает?
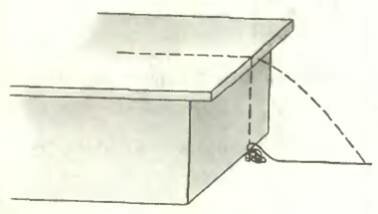
Простой опыт подтверждает справедливость нашего предположения. Мы проделали его с металлической цепочкой, которая соскальзывала с лежащего на столе листа стекла (трение в этом случае достаточно мало). Следить за падением цепочки трудно, да в этом и нет необходимости. Достаточно присмотреться к упавшей цепочке (рис. 1). Она образует на полу довольно плотный «комок» под краем стола, но от комка отходит длинный и почти прямой «хвост» перпендикулярно краю стола. Этот хвост — звенья цепочки, упавшие последними. Значит, они действительно падали не вертикально.
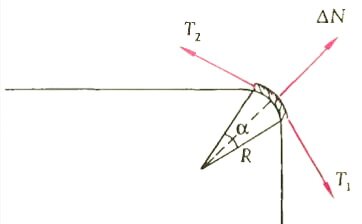
Какие же элементы шнура (или цепочки), покинув край стола, движутся все же вертикально? Рассмотрим малый участок шнура длиной Δl и массой \(~\Delta m = m \frac{\Delta l}{L}\), огибающий в данный момент край стола (рис.2). Край стола будем считать цилиндрической поверхностью радиусом R << L. На выделенный участок действуют силы упругости T1 и T2 и реакция опоры края стола ΔN (силой тяжести выбранного элемента мы пренебрегаем) . Полагая T1 = T2 = Т, запишем уравнение второго закона Ньютона в проекциях на радиальное направление:
Учитывая, что
получим \(~\Delta N = \frac{mgx \Delta l}{RL^2} (L - 2x)\).
Отсюда следует, что сила ΔN при \(~x = \frac L2\) обращается в ноль, а при больших х становится отрицательной. Реально это означает, что при \(~x = \frac L2\) шнур перестает давить на угол стола, а дальше покидающие стол элементы шнура «вылетают» в сторону.
Таким образом, полученные в самом начале формулы для скорости и ускорения шнура справедливы лишь при \(~x \le \frac L2\). А как же движется шнур дальше? Вопрос этот очень непростой, и вряд ли на него можно ответить без эксперимента (например, стробоскопической съемки падающей цепочки). Можно лишь предположить, что с увеличением высоты падения все большая часть цепочки будет переходить из комка в хвост за счет взаимодействия между частями цепочки в полете.
Примечания
- ↑ Если кто-то еще не знаком с понятием импульса тела или не умеет вычислять кинетическую энергию (о ней говорилось чуть раньше), не расстраивайтесь — все это вы узнаете очень скоро.(Прим. ред.)