Kvant. Вращательное движение

Кикоин А.К. Формулы кинематики для вращательного движениях //Квант. — 1983. — № 11. — С. 25-26.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Для описания движения материальной точки или поступательного движения твердого тела пользуются следующими кинематическими величинами: перемещением \(~\vec s\), скоростью \(~\vec \upsilon\) и ускорением \(~\vec a\). Сами они и их проекции на оси координат связаны между собой кинематическими формулами. Например, для прямолинейного равномерного движения перемещение от времени зависит так:

\(~\vec s = \vec \upsilon t\) или \(~s_x = \upsilon_x t\),

где t — время, отсчитываемое от некоторого начального момента. При прямолинейном равноускоренном движении с начальной скоростью \(~\vec \upsilon_0\) формулы кинематики имеют вид:

\(~\begin{matrix} \vec \upsilon = \vec \upsilon_0 + \vec a t \\ \vec s = \vec \upsilon_0 t + \frac{\vec a t^2}{2} \end{matrix}\) ,

или

\(~\begin{matrix} \upsilon_x = \upsilon_{0x} + a_x t \\ s_x = \upsilon_{0x} t + \frac{a_x t^2}{2} \\ \upsilon^2_x - \upsilon^2_{0x} = 2 a_x s_x \end{matrix}\) .

Но при вращательном движении тела величинами \(~\vec s\), \(~\vec \upsilon\) и \(~\vec a\) пользоваться неудобно, так как различные точки тела за один и тот же промежуток времени совершают разные перемещения и движутся с различными скоростями и ускорениями. Поэтому для описания вращательного движения вводятся специальные, так называемые угловые величины: угол поворота φ, угловая скорость ω (о них говорится в учебнике «Физика 8») и угловое ускорение \(~\varepsilon = \frac{\omega - \omega_0}{\Delta t} = \frac{\Delta \omega}{\Delta t}\) (о нем в учебнике не говорится). Для различных точек вращающегося тела они одинаковы.

Угловые величины связаны с величинами \(~\vec s\), \(~\vec \upsilon\) и \(~\vec a\), которые, в отличие от угловых, называют линейными, простыми соотношениями:

\(~\begin{matrix} s = r \varphi \\ \upsilon = r \omega \\ a = r \varepsilon \end{matrix}\) .

Здесь s — модуль перемещения данной точки тела (при малых перемещениях s — это длина дуги), r — радиус окружности, по которой она движется, υ — модуль скорости точки, а — модуль касательной проекции ускорения.

Из-за такой простой связи угловых и линейных величин кинематические формулы для вращательного движения во всем подобны кинематическим формулам, приведенным выше.

При равномерном вращении тела (угловая скорость постоянна) зависимость угла поворота φ от времени имеет вид:

\(~\varphi = \omega t\) .

При равноускоренном вращении угловая скорость ω изменяется со временем по формуле

\(~\omega = \omega_0 + \varepsilon t\) ,

где ω — начальная угловая скорость. Зависимость угла поворота от времени выражается формулой

\(~\varphi = \omega_0 t + \frac{\varepsilon t^2}{2}\) .

Точно так же между углом поворота и иловой скоростью существует связь:

\(~\omega^2 - \omega^2_0 = 2 \varepsilon \varphi\) .

Вообще любая формула кинематики вращательного движения тела получается из соответствующей формулы кинематики точки (или поступательного движения тела) простой заменой линейной величины соответствующей угловой.

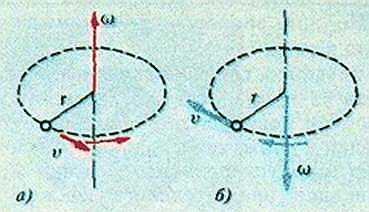
В заключение отметим (в учебнике «Физика 8» об этом не говорится), что величины φ, ω и ε тоже считаются векторными. (Нужно же отличать повороты или вращения по часовой стрелке от поворотов или вращений против часовой стрелки!) Принимается, что векторы угловых величин направлены вдоль оси вращения тела по правилу правого винта: если мысленно вращать правый винт так, как вращается тело, то направление поступательного движения винта укажет направление соответствующего вектора (см. рисунок). Правда, для углового ускорения это правило несколько усложняется: вектор ускорения совпадает по направлению с направлением движения винта, если угловая скорость возрастает по модулю, и направлен в противоположную сторону, если угловая скорость уменьшается.