Kvant. График движения при a=const
Кикоин А.К. О графике прямолинейного равноускоренного движения //Квант. — 1983. — № 10. — С. 33-35.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
При изучении механического движения широко пользуются графиками, показывающими зависимость координаты тела от времени (график движения) и скорости тела от времени (график скорости). Графики, как и соответствующие формулы, полностью описывают движение, то есть позволяют определить координату и скорость в любой момент времени. Но график имеет преимущество наглядности (построив график какой-либо функции, можно как бы «увидеть» функцию).
В учебнике «Физика 8» приведены графики движения и скорости для прямолинейного равномерного движения, а также график скорости для прямолинейного равноускоренного движения. С помощью последнего графика была получена формула для перемещения s, а значит, и для координаты х тела, движущегося равноускоренно:
Эти формулы, впрочем, можно получить и прямым вычислением (см., например, заметку «Перемещение при прямолинейном равноускоренном движении»). График же движения для этого случая не приведен, а он представляет немалый интерес. О нем и пойдет речь в этой заметке.
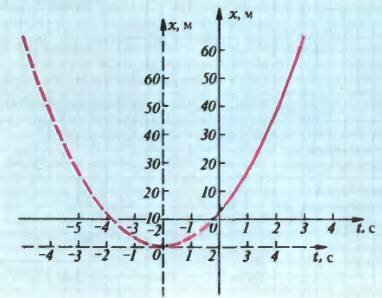
Как видно из последней формулы, выражение для координаты при равноускоренном движении — это квадратный трехчлен. В общем случае коэффициенты при t и t2 и свободный член не равны нулю. График, выражающий такую функцию, называется параболой. Ее вид и расположение относительно осей координат зависит от „трех констант — x0, υ0 и а. На рисунке 1, например, изображена парабола, соответствующая уравнению
Оно описывает прямолинейное равноускоренное движение с начальной скоростью υ0 = 12 м/с и. ускорением а = 6 м/с2. Начало отсчета времени — это момент времени, когда координата х тела (начальная координата) была равна x0 = 3 м. Графиком такого движения служит, строго говоря, лишь правая часть кривой, показанная на рисунке 1 сплошной линией. Но если бы тело двигалось по той же прямой и с тем же ускорением и до момента времени, принятого за начало отсчета, то графиком его движения была бы и левая часть кривой тоже (она показана на рисунке 1 штриховой линией).
В качестве другого примера рассмотрим движение, представленное формулой
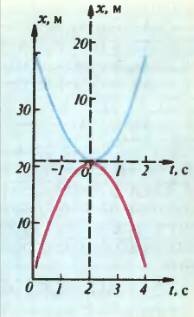
Она описывает движение тела, которому в начальный момент времени t = 0, когда его координата была равна x0 = 2 м, сообщена начальная скорость υ0 = 20 м/с и которое в дальнейшем движется с постоянным ускорением а = —10 м/с2. Это движение очень близко к движению тела, брошенного вертикально вверх (туда направлена ось X) с начальной скоростью 20 м/с с высоты 2 м над Землей. Мы лишь, для простоты, приняли ускорение свободного падения равным не 9,8 м/с2, а 10 м/с2. График этого движения приведен на рисунке 2 сплошной красной линией.
Из рисунка 2 очень ясно видно (яснее, чем из соответствующей формулы), как движется тело. Сначала оно поднимается вверх, быстро удаляясь от Земли. Через 2 секунды оно достигает максимальной высоты 22 м, после чего начинает двигаться вниз (падать). Движению вверх соответствует левая ветвь параболы, падению вниз — правая ветвь. Вообще парабола (с двумя ветвями) всегда изображает движение «туда и обратно». Синей линией на рисунке 2 показан график такого же равноускоренного движения, но с противоположно направленным ускорением.
В математике доказывается, что парабола, выражающая квадратный трехчлен вида
параллельным переносом осей координат мбжет быть преобразована в параболу, выражающую формулу
Применительно к нашему случаю для этого нужно ось t перенести вдоль оси X на расстояние, равное \(~x_0 - \frac{\upsilon^2_0}{2a}\), а ось X перенести вдоль оси t на расстояние, равное \(~- \frac{\upsilon_0}{a}\). На рисунках 1 и 2 перенесенные по этому правилу оси показаны штриховыми линиями.
Такой перенос осей означает, что за начало отсчета времени теперь принимается тот момент, когда скорость тела равна нулю (при движении «туда и обратно» такой момент обязательно существует), а за начало отсчета координаты выбирается точка, в которой в этот момент находится тело. После переноса осей парабола становится симметричной относительно оси X. Значения координаты х в момент времени t и —t и теперь одинаковы, поскольку в формулу входит только t2 и замена t на —t ничего не изменяет.
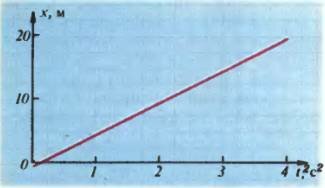
По такой параболе (в новых осях) легко найти ускорение. Ясно, что ордината точки параболы, соответствующей моменту времени t = 1, равна а/2, откуда и находим а. Ускорение а можно найти и другим путем. Если построить график зависимости х не от t, а от t2, то из формулы \(~x = \frac{a}{2} t^2\) видно, что получится прямая, проходящая через начало координат. На рисунке 3 приведен такой график для нашего случая движения тела, брошенного вверх. Значение а/2, а значит и а, можно теперь найти, взяв для любой точки графика отношение ее ординаты к абсциссе. Иначе говоря, а/2 равно тангенсу угла наклона прямой к оси t.
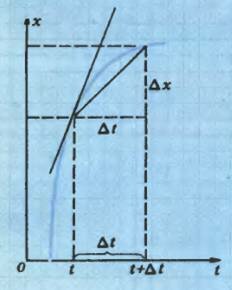
Интересна еще одна особенность параболы, позволяющая легко определять и скорость движения тела. Известно, что если график движения представляет собой прямую (прямолинейное равномерное движение), то скорость определяется углом наклона прямой к оси t. График же прямолинейного неравномерного движения — всегда кривая. Если выделить на этой кривой участок, соответствующий промежутку времени Δt и изменению координаты Δx (рис. 4), то отношение \(~\frac{\Delta x}{\Delta t}\) будет равно средней скорости за время Δt. Как видно из рисунка 4, она определяется углом наклона хорды, стягивающей выделенный участок кри вой (она равна тангенсу этого угла). Если беспредельно уменьшать промежуток времени Δt, устремляя его к нулю, то хорда перейдет в касательную к кривой в точке, соответствующей моменту времени t, а угол ее наклона определит уже мгновенную скорость в этот момент времени. Таким образом, чтобы найти по графику движения мгновенную скорость в какой-то момент времени, нужно провести касательную к графику в точке, соответствующей этому моменту, и найти тангенс угла ее наклона к оси t.
Точное проведение касательной к кривой в заданной точке (если кривая не окружность) — задача не простая. Однако в случае прямолинейного равноускоренного движения, графиком которого является парабола, для определения скорости в любой момент времени касательную можно и не проводить. Эта особенность параболы (квадратного трехчлена) связана с тем обстоятельством, что при прямолинейном равноускоренном движении средняя скорость за любой промежуток времени равна полусумме начальной и конечной скоростей. Поэтому, чтобы, пользуясь параболой, найти мгновенную скорость в какой-то момент времени, нужно выбрать промежуток времени, для которого интересующий нас момент служит серединой. Тогда средняя скорость на этот промежуток оказывается равной мгновенной скорости в середине промежутка. А чтобы найти среднюю скорость, нужно провести хорду, а не касательную, что не представляет большого труда.