Kvant. Закон всемирного тяготения3
Гросберг А. Давайте вместе откроем закон всемирного тяготения //Квант. — 1994. — № 4. — С. 2-7.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
В школе проходят, что закон всемирного тяготения открыл Ньютон. И это — как и большая часть того, что проходят в школе, — правда. Но не совсем понятно, как он это сделал. В учебниках обычно вспоминают знаменитую фразу Ньютона: «Если я видел дальше других, то потому, что стоял на плечах гигантов», и объясняют, что среди гигантов должны быть прежде всего упомянуты Галилей и Кеплер, поскольку Ньютон исходил из открытых Кеплером трех законов обращения планет вокруг Солнца и из закона (принципа) инерции Галилея. Но вопрос все-таки остается: как, исходя из этих посылок, можно было найти знаменитую формулу
Конечно, как абсолютный гений Ньютон до всего мог додуматься. Но, именно поскольку он был действительно гений, интересно проследить, каким мог бы быть конкретный ход его рассуждений. И мы можем сегодня его понять, поскольку можем и будем пользоваться хорошим и четким научным языком. А это как раз и есть тот фонарь, который позволяет простому смертному заглянуть туда, куда раньше только гений мог войти при свете своей мысли.
Среди прочего интересно понять также, какая математика нужна была Ньютону. Ведь известно, что он по ходу дела открыл и разработал дифференциальное и интегральное исчисления. Но как и для чего он эти идеи использовал? В школьном учебнике физики об этом естественно не говорится, а если взять учебник «потолще», то можно обнаружить вывод законов Кеплера из закона тяготения — но не наоборот!
Надо сказать, что с такой проблемой «наоборот» — задачей определения закона взаимодействия по данным наблюдений за движением, происходящим в результате этого взаимодействия, — Ньютон столкнулся первым из ученых, но не последним. Точнее будет сказать, что он первый так задачу поставил. Похожая проблема стояла перед Резерфордом, когда он по данным о рассеянии α-частиц на атомах золотой фольги должен был догадаться, что рассеяние происходит на самом деле на почти точечных центрах и подчиняется закону Кулона. И такая же проблема возникает в нынешней физике элементарных частиц, где по данным рассеяния одних частиц на других нужно угадать закон взаимодействия, или, если угодно, характер поля. (Такая задача называется обратной задачей рассеяния, и в ее исследовании замечательный прогресс был достигнут совсем недавно, буквально в последние годы.) Так что Ньютон и его проблемы действительно не устаревают.
Итак, давайте попробуем проследить возможный путь мысли Ньютона. Начнем с того, что вспомним законы Кеплера —
- 1-й закон: орбита любой планеты — эллипс, в одном из фокусов которого находится Солнце;
- 2-й закон: радиус-вектор планеты в равные промежутки времени описывает равные площади;
- 3-й закон: квадраты периодов обращений двух планет вокруг Солнца относятся как кубы больших полуосей их орбит. (Заметим, что по современным данным отношение \(~\frac{T^2}{R^3}\) равно k = (2,973 ± 0,005)·10-19 с2/м3.)
Вспомним также принцип инерции Галилея — при отсутствии внешних воздействий (сил) тело сохраняет неизменным состояние своего движения (т.е. остается неизменной скорость тела как по величине, так и по направлению).
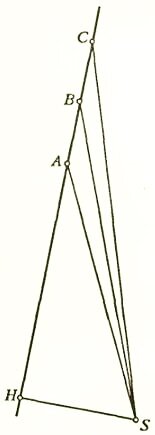
Спрашивается: что можно вывести логически из этих посылок и какие новые гипотезы пришлось ввести Ньютону? Первым шагом было сопоставление принципа инерции Галилея со вторым законом Кеплера. В самом деле, рассмотрим ситуацию, о которой говорится в принципе Галилея — никакая сила не действует. Сохраняется ли так называемая секторная скорость, т.е. скорость возрастания площади, описываемой радиусом-вектором движущейся точки? Да — в этом легко убедиться, глядя на рисунок 1. Условное Солнце (не создающее никакой силы) находится в точке S, точки A, B, C изображают положения условной планеты через равные промежутки времени Δt, скажем через 1 сутки. Сохранение секторной скорости означает равенство площадей секторов SAB и SBC. И они действительно одинаковы: поскольку в отсутствие силы сохраняется направление скорости, то отрезки АВ и ВС принадлежат одной прямой, следовательно, треугольники SAB и SBC имеют общую высоту SH, но основания их тоже равны, так как сохраняется и величина скорости, т.е. AB = BC = υΔt, откуда и вытекает равенство площадей.
А если сила действует и скорость меняется? Например, если бы сила действовала вдоль прямой АС, то скорость менялась бы по абсолютной величине, отрезки АВ и ВС были бы различны и секторная скорость бы не сохранялась. Ньютон догадался: из второго закона Кеплера вытекает, что сила действует в направлении прямой, соединяющей планету с Солнцем.
Ну вот, скажет читатель, тоже мне открытие: куда она, собственно, еще могла бы действовать? Да куда угодно! Представьте себе, что в наше время некто занят исследованием «планетной системы» вокруг Земли — он не знает, что это на самом деле искусственные спутники, и изучает их движение. Он может открыть, что некоторое возмущение какого-то поля, исходящее из центрального тела (Земли), т.е. то, что па самом деле является управляющим радиосигналом, вызывает силу, действующую на спутник в разных случаях по разным направлениям — иногда по касательной к орбите, иногда под углом и т.д. Это уже потом наш не очень грамотный исследователь откроет для себя, что на самом деле сила появляется и совершает работу за счет энергии, запасенной внутри спутника в виде химической энергии топлива, а возмущение электромагнитного поля играет роль только информационную, сигнальную. Но это потом, а пока что он может предположить псе что угодно. И во времена Ньютона очень правдоподобно выглядело бы предположение, что вокруг планеты, махая крылышками, летают ангелы и равнодействующая их сил направлена...
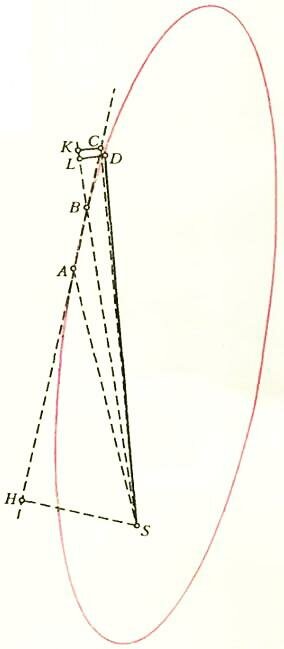
Итак, Ньютон формулирует теорему: раз секторная скорость планеты сохраняется, значит, сила, действующая на планету, направлена по прямой к Солнцу. Для доказательства обратимся к рисунку 2. Планетная орбита на нем чрезмерно вытянута — так выглядят на самом деле орбиты не планет, а комет. Но, во-первых, кометы тоже подчиняются законам Кеплера, хотя Кеплер этого и не знал (а кометы не знают этого и по сей день), а во-вторых, «геометрия — это искусство правильно рассуждать на неправильно построенном чертеже» (А. Пуанкаре). Здесь же пунктиром воспроизведен и рисунок 1, но теперь планета из точки В двигалась не вдоль той же прямой в точку С, а под действием силы завернула и попала в точку D. При этом секторная скорость сохранилась, т.е. площадь треугольника SBD равна площади треугольника SAB, или, в силу сказанного раньше, площади треугольника SBC. Треугольники SBC и SBD имеют общую сторону SB, поэтому из равенства их площадей вытекает равенство соответствующих высот: CK = DL. Это, в свою очередь, означает, что линия CD параллельна прямой BS. А что, собственно, такое CD? Давайте решим этот вопрос с помощью векторов:
где \(~\vec \upsilon_{AB}\) и \(~\vec \upsilon_{BD}\) — средние скорости планеты на соответствующих участках траектории; следовательно,
т.е. вектор \(~\vec{CD}\) коллинеарен вектору изменения скорости. Отсюда вытекает, что вектор изменения скорости направлен вдоль прямой BS — как раз от планеты к Солнцу! А поскольку изменение скорости, согласно Галилею, вызывается силой, то разумно предположить, что сила направлена туда же, куда и изменение скорости, т.е. к Солнцу.
Подведем предварительные итоги. Мы доказали (вполне строго), что из равенства площадей треугольников SAB и SBD вытекает, что векторная разность средних скоростей планеты на участках АВ и BD направлена вдоль BS, т.е. к Солнцу. Но в рассуждении имеются две слабости. Во-первых, утверждение о сохранении секторной скорости неизменной означает совпадение площадей криволинейных фигур SAB и SBD, ограниченных не прямолинейными отрезками АВ и BD, а соответствующими дугами — участками эллиптической орбиты. Хотя совершенно очевидно, что соответствующая ошибка становится ничтожной, если мы рассматриваем достаточно маленький отрезок времени Δt, и, кроме того, Кеплер по данным наблюдения все равно не мог ничего сказать о точной площади криволинейных фигур и тоже заменял их обычными треугольниками, но все же для превращения теоремы в совсем строгую требуется чуть-чуть аккуратности с предельным переходом \(~\Delta t \to 0\). Это первое, но не главное место, для которого Ньютону потребовался новый математический аппарат.
Во-вторых, и это гораздо более важно, доказанная теорема касается изменения скорости, т.е., как мы теперь понимаем, ускорения, и потребовалась физическая гипотеза, что ускорение направлено вдоль линии действия силы. Таким образом, можно предположить, что шаг ко второму закону Ньютона был сделан одновременно с шагом к закону всемирного тяготения.
Надо сказать, что с современной точки зрения все это совсем просто: постоянство секторной скорости — это сохранение момента импульса, а сохраняется он только для случая центральной силы. Тот же закон сохранения объясняет, почему планетная орбита плоская (о чем Кеплер и Ньютон, насколько известно автору, не задумывались). Правда, он не объясняет, почему плоскости орбит разных планет почти совпадают — возможно, этот факт говорит нам что-то уже не просто о механике, а об истории возникновения Солнечной системы как о процессе, протекавшем так, что практически вся масса чего-то исходного (тумана? сгустка?... ?) сосредоточилась в центре (Солнце), а момент импульса распределился по периферии. Но мы отвлеклись от темы.
Двигаемся дальше. Если сила направлена от планеты к Солнцу, то как она зависит от расстояния планета — Солнце? Естественно искать ответ на этот вопрос в третьем законе Кеплера, потому что именно он говорит о поведении планет на разных расстояниях от Солнца. Для этого, правда, нужно верить, что у всех планет закон изменения силы с расстоянием один и тот же. Быть может, это место было самым трудным. Впрочем, это уже область гадания. А рассуждать дальше можно так. Как мы знаем из принципа Галилея, чем больше действующая сила, тем сильнее меняется скорость тела, т.е. тем больше его ускорение. Подсчитаем же ускорение для планеты — то самое, которое теперь называется центростремительным ускорением.
Обозначим искомую силу, зависящую от расстояния R, через F(R) и допустим, что она пропорциональна центростремительному ускорению \(~a = \frac{\upsilon^2}{R} = \frac{4 \pi^2 R}{T^2}\) . Это естественное предположение, потому что мы знаем из принципа Галилея, что ускорение должно расти с ростом силы, и, кроме того, предположение о векторной коллинеарности силы и ускорения уже сделано — сказав «а», нужно сказать и «б». При таком допущении мы получаем
где m — пока просто какой-то коэффициент, и отсюда мгновенно находим простую формулу для периода обращения или лучше сразу для квадрата периода, поскольку именно эта величина входит в третий закон Кеплера:
Составляя теперь кеплерову комбинацию \(~\frac{T^2}{R^3}\), мы получаем, что величина \(~\frac{F(R) R^2}{m}\) должна быть одинаковой для всех планет. В частности, она не должна зависеть от R, откуда сразу следует, что зависимость силы от расстояния подчиняется закону обратных квадратов:
Снова подведем итоги. Мы уже продвинулись довольно далеко. Из второго закона Кеплера мы определили направление действия силы, а из третьего — зависимость величины силы от расстояния: если вспомнить одинаковую для всех планет постоянную Кеплера
то получается
Как можно было проверить этот результат? Здесь Ньютон сделал шаг поразительной интеллектуальной смелости (правда теперь кажущийся совершенно естественным). Он предположил, что формула (*) с равным успехом годится для описания притяжения не только планеты к Солнцу, но и Луны к Земле, только величина k может быть другой — обозначим ее kz. Тогда, поскольку \(~\frac Fm\) есть ускорение (так было введено m), а движение Луны — вращательное с ускорением, равным \(~\frac{4 \pi^2 R_L}{T^2_L}\), то получается просто снова третий закон Кеплера:
но уже не для Солнечной системы, а для «Земной». Радиус орбиты Луны RL и период ее обращения TL — величины, которые Ньютон хорошо знал: TL ≈ 28 суток, RL ≈ 3,8·108 м. В результате получается kz ≈ 9,87·10-14 с2/м3.
Ну и что? Другого-то спутника у Земли нет — только Луна, сравнить результат вроде бы не с чем. Вот тут- то и приходит черед знаменитого яблока из старого анекдота, согласно которому закон всемирного тяготения был открыт в саду, когда Ньютону на голову упало яблоко. Ньютон догадался, что обычное падение тел на Землю вызвано силой той же природы, что и тяготение планет к Солнцу, и поэтому ускорение свободного падения — всем современным школьникам известное g ≈ 9,8 м/с2 — должно быть равно отношению \(~\frac Fm\) из формулы (*), но только в качестве R нужно взять расстояние от тела до центра Земли, т.е. попросту радиус Земли Rz. А эту величину измеряли еще греки, и Ньютон знал, что Rz ≈ 6400 км. В итоге получается
что прекрасно согласуется со значением 9,8 м/с2.
Это первый момент торжества: стартовав от астрономических законов обращения планет и сделав всего два допущения, Ньютон вычислил величину g, измеренную совершенно независимо в земных условиях, — и получил правильный ответ. Такое вряд ли могло быть случайным совпадением. По-видимому, предположения Ньютона правильные. Напомним их еще раз. Первое\[~\vec F = m \vec a\] — предположение, сделанное в два приема, сначала для направлений векторов и потом для их модулей; второе: сила одной и той же природы действует на планеты со стороны Солнца, на Луну со стороны Земли и, наконец, на яблоки и прочие земные предметы. Если первое можно, пожалуй, считать до некоторой степени естественным обобщением принципа Галилея, то второе иначе как гениальным прозрением не назовешь.
Что же было дальше? А дальше Ньютон догадался, что коэффициент m — это масса тела, потому что она определяет как раз меру инертности. Собственно, определения массы тогда не существовало, и Ньютон просто назвал коэффициент m этим словом. Потом он понял, что ситуация должна быть симметричной, и если сила тяготения пропорциональна массе одного из тел, то должна быть пропорциональна и массе второго, т.е. М. Все же остальные коэффициенты есть просто мировая постоянная G, так что получается всем известное соотношение
а также
и
Когда через сто с лишним лет после открытия Ньютоном закона всемирного тяготения Кавендишу удалось измерить гравитационное притяжение на опыте и получить тем самым значение G, то из этих формул он смог найти массы Солнца и Земли:
— «взвесил» Солнце и Землю.
Но мы отвлеклись. По нашему рассказу получилось, что для открытия закона всемирного тяготения было достаточно знать второй и третий законы Кеплера (и то только для круговых орбит), а первый вроде бы и ни к чему. А сколько сил и сколько лет труда ушло у Кеплера на первый закон!
Только представьте себе, как он работал. В распоряжении Кеплера было несколько сотен чисел — данные астрономических измерений, преимущественно Тихо Браге, и задача состояла в том, чтобы угадать уравнение кривой по данным о координатах некоторого числа ее точек (тоже своего рода обратная задача). Кеплер брал какую-нибудь гипотезу о форме орбиты и, варьируя параметры (например, радиусы в случае круговых орбит), вычислял для каждого значения параметров соответствующие сотни ожидаемых значений результатов угловых измерений — и сравнивал их с имеющимися. Если не получалось, выбирал новое значение параметра и начинал вычисления с самого начала. Конечно, данные были, мягко говоря, не без погрешностей (они же были получены без телескопов!), так что Кеплер должен был почувствовать, какими отклонениями можно пренебречь, а какие необходимо принять во внимание.
Наибольшие хлопоты доставил Кеплеру Марс — на самом деле потому, что у него довольно вытянутая орбита, сильно отличающаяся от круговой. Кеплер представлял себе, что он сражается с самим Богом войны Марсом. Вот как он, например, описал момент, когда не сработала уже казавшаяся правильной гипотеза об эллиптической форме орбиты с Солнцем в центре эллипса (а не в фокусе!): «В то время, как я упивался триумфом, одержанным над движениями Марса, словно тот был уже окончательно побежден, заключен в темницу таблиц и сплетен путами уравнений, из разных мест стали приходить сообщения о том, что победа была лишь призрачной, и война разгорелась с новой силой. В стенах моего дома враг, которого я уже считал пленником, разорвал путы уравнений и взломал темницу таблиц... Снаружи шпионы, расставленные вдоль орбиты (я имею в виду истинные расстояния), одолели вызванные мной... войска физических причин, сбросили их гнет и вновь обрели свободу. Еще немного, и бежавший враг примкнул бы к восставшим, что привело бы меня в отчаяние. Не теряя ни минуты, я тайно выслал вперед подкрепление — полки новых физических причин, со всей поспешностью разведал, в каком направлении скрылся беглец, и стал преследовать его по пятам».
Неужели такой труд пропал даром? К счастью, это совсем не так. В самом деле, чтобы догадаться до формулы (*), было достаточно второго и третьего законов Кеплера. И была опора с другой стороны — связанная с вычислением g. Но она была слишком слабой для логического «моста», на который предполагалось водрузить тяжесть научной теории всего мироздания — а Ньютон претендовал именно на это. Было крайне важно найти какой-то способ проверки теории. Вот тут-то и пригодился первый закон Кеплера. Задача теперь ставилась так. Допустим, что сила подчиняется формуле (*). Какова тогда будет форма орбит? И Ньютон доказал, что орбиты будут эллиптическими (или гиперболическими для быстро летящих тел вроде некоторых комет) и что в третий закон Кеплера будут входить именно большие полуоси, а не какие-нибудь иные расстояния.
Вот это и был главный момент торжества. И он продолжался много-много лет:
- — и когда комета Галлея, подчиняясь предсказаниям формулы (*), стала возвращаться в пределы видимости каждые 76 лет;
- — и когда Адамс и Леверье открыли новую планету не глядя в телескопы, ас помощью вычислений, — и Нептун им подчинился, оказавшись точно в той точке неба и в то время, которое предсказала формула (*);
- — и когда уже в нашем веке удалось в течение нескольких лет фотографировать положения системы двух близких звезд и увидеть замечательно правильную эллиптическую форму орбиты...
Если же говорить об истории, то, к сожалению, красивая легенда о великом ученом, скромно отдающим дань предшественникам, ставится специалистами под сомнение. Есть очень веские основания думать, что знаменитая фраза насчет гигантов была всего только грубой попыткой оскорбить Гука (который был маленького роста) в связи с тем. что уже после опубликования знаменитой книги Ньютона «Математические начала натуральной философии» и признания закона всемирного тяготения Гук напомнил, что он, хотя всего закона и не открыл, но некоторые правильные мысли в этом направлении высказывал. В частности, известно, что Ньютон не первым догадался до «закона обратных квадратов» — об этом действительно говорил Гук и некоторые другие. Тем ие менее абсолютное и полное главенство Ньютона никакого сомнения не вы зыкает Почему?
Во-первых, Ньютон первым доказал, что из закона обратных квадратов вытекает эллиптичность орбит. Только узнав о существовании такого доказательства, Галлей (открывший комету, носящую теперь его имя) сумел уговорить Ньютона опубликовать его результаты, пролежавшие до того без движения несколько десятилетий (I). Во-вторых, Ньютону принадлежит сама идея всемирности тяготения — идея о том, что тяготеют все тела в мире. В-третьих, и в главных, книга Ньютона была (и является) цельным сооружением, великолепным дворцом, где прекрасно и соразмерно все — общий подход («метод принципов»), широта взгляда (планеты — приливы — яблоки), философская глубина (взять хотя бы вопрос о массе, где Ньютон четко объяснил три аспекта этого понятия, связанные с количеством вещества, инертностью и гравитационным «зарядом», математический аппарат. Словом, это действительно огромный и прекрасный дворец. А каждый отдельный кирпич, окно или колонна — очень важны, но ... это только детали. «Наука состоит из фактов, подобно тому, как здание — из кирпичей. Но простое собрание фактов похоже на науку не более, чем груда кирпичей надом» (А. Пуанкаре). И конечно же, Ньютон, с его поразительной трудоспособностью и ни с чем не сравнимыми достижениями в науке.был подлинным украшением рода человеческого, как это написано на его могиле в Вестминстерском аббатстве в Лондоне. А если мы считаем, что споры о приоритете не украшают никого, и пытаться дразнить человека маленького роста, называя его гигантом, глупо даже в детском саду — то, видно, таково уж человечество, если украшающий его Ньютон себе это позволял...
Ну хорошо, а как же все-таки Ньютон вывел эллиптичность орбит из формулы ( * )? Казалось бы, наконец, дошла очередь до настоящего применения нового математического аппарата. Но это — уже совсем другая история.