Kvant. Запуск спутника

Ланге В. Сколько стоит запуск спутника? //Квант. — 2002. — № 5. — С. 30-31.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Рассмотрим спутник, обращающийся вокруг Земли по сравнительно низкой круговой орбите, во всех точках которой ускорение силы тяжести можно считать равным его значению вблизи земной поверхности, т.е. g = 9,8 м/с². Учитывая, что центростремительное ускорение спутнику сообщает сила притяжения к Земле:

\(~\frac{m \upsilon^2}{R} = mg\) ,

где m - масса спутника, υ — его скорость, R - радиус Земли, находим кинетическую энергию спутника:

\(~E_k = \frac{m \upsilon^2}{2} = \frac{mgR}{2}\) .

Для оценки потенциальной энергии спутника, движущегося по низкой орбите, используем приближение

\(~E_p = mgH\) ,

где высота орбиты Н << R.

Сравнивая два последних выражения, мы видим, что потенциальная энергия спутника на низкой орбите намного меньше его кинетической энергии, которую, таким образом, можно считать практически равной полной энергии спутника Е. Найдем ее, положив m = 100 кг и R = 6,4·10⁶ м :

Е = 0,5 · 100 кг · 9,8 м/с² · 6,4·10⁶ м = 3,1·10⁹ Дж = 870 кВт·ч,

при тарифе, например, 56 копеек за 1 киловатт-час запуск спутника должен, казалось бы, стоить всего около 480 рублей! Почему же на самом деле затраты на осуществление космических программ соизмеримы с национальными бюджетами небольших стран?

Разгадка парадокса состоит в том, что полученное нами значение энергии, 870 кВт·ч , необходимо, но совершенно недостаточно для запуска спутника массой 100 кг на околоземную орбиту. Поскольку ракета как тепловая машина обладает крайне низким коэффициентом полезного действия, фактические затраты энергии оказываются во много-много раз больше. Дело в том, что наряду с полезным грузом приходится поднимать также горючее, необходимое для непрерывной работы двигателей. Правда, ракета «худеет» очень быстро, но для сообщения ей желательной скорости нужно сжечь колоссальные количества топлива, что сильно снижает КПД.

Для вывода формулы, связывающей массу и скорость ракеты, примем сначала, что топливо сгорает отдельными порциями массой \(~\Delta M = \frac MN\), где М - масса ракеты перед выбросом из нее порции ΔМ, а N - достаточно большое число. После сгорания первой порции масса ракеты станет равной

\(~M_1 = M_0 - \frac{M_0}{N} = M_0 \left( 1 - \frac 1N \right)\) .

После сгорания второй Порции масса вновь уменьшится на \(~\frac 1N\)-ю часть, но уже от M₁, и станет равной

\(~M_2 = M_1 \left( 1 - \frac 1N \right) = M_0 \left( 1 - \frac 1N \right)^2\) .

Рассуждая таким же образом далее, находим массу ракеты после сгорания n-й порции топлива:

\(~M_n = M_0 \left( 1 - \frac 1N \right)^n\) . (1)

Рассмотрим теперь, как меняется при этом скорость ракеты. При скорости истечения продуктов горения, равной u, масса ΔМ уносит импульс Δp = uΔМ. В соответствии с законом сохранения импульса такой же по величине, но противоположно направленный импульс получит ракета, в результате чего ее скорость увеличится на \(~\frac{\Delta p}{M - \Delta M} = \frac{u \Delta M}{M - \Delta M}\). Таким образом, если вначале ракета покоилась, то после сгорания первой порции массой \(~\Delta M_1 = \frac{M_0}{N}\), имевшей импульс \(~\Delta p_1 = \frac{M_0 u}{N}\), скорость ракеты станет равной

\(~\upsilon_1 = \frac{\Delta p_1}{M_1} = \frac{u}{N - 1}\) .

После сгорания второй порции топлива массой \(~\Delta M_2 = \frac{M_1}{N}\), унесшей импульс \(~\Delta p_2 = \frac{M_1 u}{N}\), скорость ракеты возрастет на \(~\frac{\Delta p_2}{M_1 - \frac{M_1}{N}}\) и составит

\(~\upsilon_2 = \upsilon_1 + \frac{u}{N - 1} = \frac{2u}{N - 1}\) .

Продолжая рассуждения далее, получим скорость ракеты после сгорания n-й порции:

\(~\upsilon_n = \frac{nu}{N - 1}\) . (2)

Из равенств (1) и (2) получаем массу ракеты, достигшей скорости υ:

\(~M = M_0 \left( 1 - \frac 1N \right)^{\frac{\upsilon(N - 1)}{u}}\)

(индекс n здесь и далее опущен, поскольку надобности в нем больше нет).

На самом деле топливо в ракете сгорает не отдельными порциями, а непрерывно. Для перехода к формуле, более правильно описывающей реальный случай, нужно считать N чрезвычайно большим числом. В таком случае единицей в показателе степени последнего выражения можно пренебречь, после чего оно приобретает вид

\(~M = M_0 \left( 1 - \frac 1N \right)^{\frac{\upsilon N}{u}} = M_0 \left( \left( 1 - \frac 1N \right)^N \right)^{\frac{\upsilon}{u}}\) ,

или при неограниченном возрастании

\(~M = M_0 e^{-\frac{\upsilon}{u}}\) .

Эта формула была выведена К.Э.Циолковским и носит его имя. Из нее хорошо видно, что ракета может достичь большой скорости, но при этом оставшаяся масса окажется много меньше первоначальной.

Пользуясь формулой Циолковского, можно оценить, сколько горючего нужно сжечь, чтобы сообщить ракете необходимую скорость. Однако для этого следует знать относительную скорость истечения газов из сопла ракеты. Чтобы найти ее, приравняем кинетическую энергию небольшой массы Δm газа, вылетевшей из ракеты за малый интервал времени, той химической энергии, которой обладала эта масса до того, как она сгорела. Обозначив теплоту сгорания (теплотворную способность) топлива через q, получим равенство

\(~\frac{\Delta m u^2}{2} = \Delta mq\) ,

откуда

\(~u = \sqrt{2q}\) .

Теплота сгорания смеси керосина с азотной кислотой, иногда используемой в ракетной технике, составляет приблизительно 6,3 МДж/кг, и скорость истечения, следовательно, не может превысить

\(~\sqrt{2 \cdot 6,3 \cdot 10^6}\) (Дж/кг)^1/2 = 3,55 км/с.

Одна из самых больших возможных скоростей истечения достигается при использования реакции горения металлического бериллия в атмосфере кислорода:

Be + 0,5 О₂ = ВеО + 0,612 Мдж .

Число мегаджоулей справа показывает, какая энергия выделяется при взаимодействии одного моля бериллия (9 г) с половиной моля кислорода (16 г). Стало быть, теплота сгорания в этом случае равна 0,612 МДж / 0,025 кг = 24,5 МДж/кг, а наибольшая скорость истечения газов составляет

\(~\sqrt{2 \cdot 24,5 \cdot 10^6}\) (Дж/кг)^1/2 = 7 км/с.

Однако в дальнейших расчетах мы примем скорость истечения равной всего 2,5 км/с, поскольку, во-первых, такие энергетически выгодные реакции, как окисление бериллия, использовать невозможно из-за высокой токсичности и самого бериллия и его соединений, а во-вторых, фактическая скорость истечения всегда оказывается меньше максимальной.

Теперь по формуле Циолковского находим, что при достижении, например, первой космической скорости (7,9 км/с) конечная масса ракеты окажется равной

\(~M = M_0 e^{-\frac{7,9}{2,5}} = \frac{M_0}{e^{3,6}} = \frac{M_0}{37}\) .

Иначе говоря, масса горючего должна составлять 36/37 = 97,5% от стартовой массы ракеты. Естественно, что на долю действительно полезного груза (экипаж, приборы и т.п.) остается совсем немного. Вот почему для уменьшения бесполезной массы, которую пришлось бы разгонять до большой конечной скорости, ракеты (по идее, впервые выдвинутой также Циолковским) делают многоступенчатыми, причем нижние ступени сбрасываются, когда в них кончается топливо.

Для окончательной оценки затрат на запуск ракеты введем коэффициент полезного действия, определив его как отношение кинетической энергии массы ракеты, оставшейся к моменту достижения нужной скорости, к химической энергии сгоревшего топлива:

\(~\eta = \frac{\frac{M \upsilon^2}{2}}{(M_0 - M)q} = \frac{\upsilon^2}{2\left( \frac{M_0}{M} - 1 \right)q}\) .

Пользуясь формулой Циолковского и выражением для максимальной скорости истечения газов, получим, обозначив отношение \(~\frac{\upsilon}{u}\) через k, следующее соотношение:

\(~\eta = \frac{\upsilon^2}{u \left( e^{\frac{\upsilon}{u}} - 1 \right)} = \frac{k^2}{e^k - 1}\) .

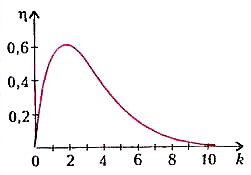
График зависимости η от k показан на рисунке. Из него хорошо видно, что при скорости ракеты, заметно превышающей скорость истечения газов, коэффициент полезного действия становится очень малым. Например, при k = 10 коэффициент составляет 0,45%. Это уже малая величина, но в действительности дело обстоит еще во много раз хуже.