Kvant. За пределами закона Ома
Магазин MEGA-KERATIN предлагает средства для бразильского выпрямления.
Мурзин С., Трунин М., Шовкун Д. За пределами закона Ома //Квант. — 1989. — № 4. — С. 2-8.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
«Бди!»— чаще пользуйтесь этим советом Козьмы Пруткова, когда речь идет о законах. В частности — о законах физики. Вспомним, например, закон Ома: ток пропорционален напряжению. Оказывается, бывает и не так. И хорошо! Если бы этот закон соблюдался всегда, то мы остались бы без многих электро- и радиотехнических устройств. К счастью, закон Ома, как и большинство законов физики, имеет ограниченную область применимости. Именно за пределами действия этого закона и возникают интересные физические явления, обеспечивающие работу этих устройств. Сами по себе эти явления очень интересны, но сегодня мы обсудим другой вопрос: из-за чего нарушается закон Ома?
Закон Ома
Включим проводник в электрическую цепь и будем измерять силу тока I, текущего по проводнику, при разных значениях приложенного напряжения U. Таким образом мы получим зависимость I = I(U) — вольт-амперную характеристику проводника. Согласно закону Ома, сила тока прямо пропорциональна приложенному напряжению, т. е. вольт-амперная характеристика представляет собой линейную функцию
и сопротивление R не зависит от U. Если же это не так (закон Ома не выполняется), то вольт-амперная характеристика нелинейная.
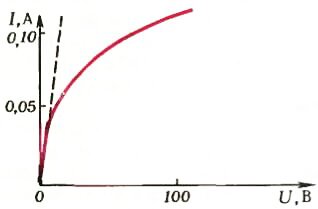
Самым простым примером проводника, в котором нарушается закон Ома, является спираль лампы накаливания. Для лампы мощностью 40 Вт вольт-амперная характеристика приведена на рисунке 1. Линейный участок имеется лишь при U < 5 В, а при больших значениях U ток I растет медленнее, чем в случае линейной зависимости I(U). Нетрудно догадаться, почему так получается. При повышении напряжения спираль разогревается, и ее сопротивление увеличивается. Этот пример иллюстрирует общее правило: закон Ома справедлив лишь при достаточно малых I и U, а при больших токах и напряжениях он нарушается.
Запишем закон Ома в другом виде. Для этого введем величину плотности тока \(~j = \frac IS\), где S — площадь сечения проводника. Тогда
Здесь ρ — удельное сопротивление проводника, величина \(~\sigma = \frac{1}{\rho}\) называется удельной проводимостью, L — длина проводника, \(~E = \frac UL\) — напряженность электрического поля. Закон Ома предполагает линейную связь между плотностью тока j и напряженностью электрического поля Е. Если же проводимость а по какой-то причине зависит от величины электрического поля, то зависимость j от Е становится нелинейной, и закон Ома нарушается.
Чтобы выяснить причины нарушения закона Ома, рассмотрим движение электронов в проводниках в отсутствие и при наличии электрического поля.
Как электроны движутся в проводнике
Многие вещества, проводящие электрический ток, являются кристаллическими. Атомы, из которых они состоят, занимают не случайные положения, а образуют структуру, периодически повторяющуюся в пространстве,— кристаллическую решетку.
В проводниках часть атомов ионизована, а оторвавшиеся от них электроны могут перемещаться по проводнику. Концентрация п таких электронов (их называют электронами проводимости) зависит от типа проводника. В металлах концентрация электронов проводимости от температуры не зависит. В меди n = 8,4·1028 м-3. В полупроводниках п зависит от температуры. При Т = 300 К в германии n = 2,4·1019 м-3.
Может показаться, что электрон с большим трудом «протискивается» через кристалл, то и дело натыкаясь на атомы. Но это совсем не так. Из квантовой теории следует, что из-за строго периодического расположения атомов электроны будут двигаться сквозь идеальную решетку прямолинейно. Этим электроны проводимости напоминают свободные электроны в вакууме. И так же, как в случае электронов в вакууме, движение электронов в кристалле можно описывать с помощью II закона Ньютона — F = m*a, только масса m* в этой записи (ее называют эффективной массой) отличается от массы me электрона в вакууме. Это отличие отражает взаимодействие электрона проводимости с кристаллической решеткой. Поскольку структуры решеток различны в разных проводниках, то и эффективные массы электрона в них будут отличаться. При этом m* может быть как больше, так и меньше me.
Реальные проводники никогда не являются идеальными кристаллами. В них всегда есть нарушения периодического расположения атомов. Например, в некоторые места решетки случайно попадают атомы постороннего вещества — примеси. Налетев на такую примесь, электроны рассеиваются, т. е. изменяют направление своего движения. Тепловые колебания атомов решетки (их отклонения от положений равновесия) нарушают периодичность, и это тоже приводит к рассеянию электронов. Среднее время между столкновениями, в течение которого электрон движется прямолинейно, называется временем свободного пробега τ. Время τ зависит от скорости электрона.
В отсутствие электрического поля электроны проводимости перемещаются в разных направлениях, совершая хаотическое тепловое движение. В полупроводниках движение электронов подобно тепловому движению молекул идеального газа. Средняя скорость υ0 такого движения находится из условия \(~\frac{m^* \upsilon^2_0}{2} = kT_e\), где k — постоянная Больцмана, Te — температура электронов. При Te ≈ 300 К в арсениде галлия (GaAs) υ0 ≈ 4,5·105 м/с.
В металлах, где концентрация электронов значительно больше, чем в полупроводниках, нельзя пользоваться выводами молекулярно-кинетической теории газов. Как следует из квантовой теории, средняя скорость хаотического движения электронов в металлах υ0 ≈ 106 м/с и практически не зависит от температуры.
Теперь посмотрим, к чему приведет включение электрического поля \(~\vec E\) . Действующая на электрон сила \(~-e \vec E\) сообщает ему ускорение \(~\vec a = -\frac{e \vec E}{m^*}\). Обозначим скорость i-го электрона сразу после рассеяния \(~\vec \upsilon_i\). В произвольный момент времени скорость i-го электрона будет равна \(~\vec \upsilon_i - \frac{e \vec E}{m^*} t_i\), где ti — время, прошедшее с момента последнего столкновения. Средняя скорость N электронов —
Величина \(~\frac 1N \sum^N_{i=1} \vec \upsilon_i\) есть средняя скорость электронов сразу после рассеяния. Так как скорости электронов сразу после рассеяния могут быть направлены в любую сторону, \(~\frac 1N \sum^N_{i=1} \vec \upsilon_i = 0\). Величина \(~ \frac 1N \sum^N_{i=1} t_i = \tau\) имеет смысл уже знакомого нам среднего времени свободного пробега. Итак, под действием электрического поля все электроны приобретают добавочную скорость (ее называют дрейфовой), среднее значение которой равно \(~u = \frac{eE \tau}{m^*}\), и направлена эта скорость параллельно полю \(~\vec E\).
Таким образом, при наличии электрического поля на хаотическое движение электронов накладывается дрейфовое, появляется преимущественное направление движения электронов — возникает электрический ток. Если концентрация электронов в проводнике равна n, то плотность этого тока —
С другой стороны, мы знаем, что \(~j = \sigma E\). Значит,
Эта формула называется формулой Друде. Закон Ома справедлив, если ни одна из величин, входящих в формулу Друде, не зависит от Е. Если же концентрация электронов n или время свободного пробега τ, или эффективная масса m* изменяются под действием электрического поля, то закон Ома нарушается.
Когда же справедлив закон Ома
Прежде всего рассмотрим, при каких условиях величина τ не меняется под действием поля Е.
Время τ зависит от скоростей электронов. Дрейфовая скорость \(~u = \frac{eE \tau}{m^*}\), появляющаяся при включении электрического поля, возрастает при увеличении Е. Пока электрическое поле мало, так что дрейфовая скорость и гораздо меньше средней скорости хаотического движения υ0, величиной u можно пренебречь и считать время τ не зависящим от поля Е. Если же Е велико настолько, что значение u сравнимо с υ0, to дрейфовую скорость нужно учитывать. В этом случае скорости электронов и, следовательно, время свободного пробега τ оказываются зависящими от электрического поля.
Таким образом, для выполнения закона Ома необходимо, чтобы выполнялось условие
т. е. напряженность электрического поля в проводнике должна быть много меньше \(~E = \frac{m^* \upsilon_0}{e \tau}\).
В полупроводниках, как мы уже говорили, υ0 ~ 106 м/с. Чтобы достичь значения u, сравнимого с υ0, к полупроводнику необходимо приложить поле E ~ 106 В/м. Это — огромная величина, сравнимая с напряженностью поля в молнии. Тем не менее такое поле удается создать в полупроводниках.
Есть еще одно, более сильное ограничение на скорость u. Она должна быть меньше скорости звука в проводнике (а υzv ~ 103 м/с):
Как только скорость u достигает значения υzv, в кристалле возбуждаются звуковые колебания. При этом время свободного пробега τ и проводимость σ, пропорциональная τ, могут уменьшиться. Эта ситуация аналогична резкому увеличению аэродинамического сопротивления после преодоления самолетом звукового барьера.
Итак, в поле \(~E \ge \frac{m^* \upsilon_{zv}}{e \tau}\) проводимость начинает зависеть от величины Е, и закон Ома нарушается.
Действие электрического поля не сводится только к появлению дрейфового движения. Известно, что при протекании тока в проводнике выделяется джоулево тепло, и он нагревается. Рассмотрим этот процесс подробнее.
Любой проводник можно считать состоящим из двух подсистем: кристаллической решетки, образованной атомами вещества, и газа электронов проводимости, заполняющего решетку. Электроны и решетку можно характеризовать своими температурами Te и Tp. В отсутствие электрического поля электронный газ находится в тепловом равновесии с решеткой и окружающей средой: Te = Tp = Tc. Поле Е действует на электроны проводимости и разогревает прежде всего их. Лишь затем от электронов тепло передается решетке, а потом окружающей среде. Поэтому при наличии поля тепловое равновесие нарушается так, что Te > Tp > Tc.
Если теплопередача от проводника окружающей среде хуже теплопередачи от электронов атомам и, следовательно, \(~T_e - T_p \ll T_p - T_c\), то решетка вместе с электронами разогревается как целое. (Такая ситуация характерна для спирали лампы накаливания.) Возможен и обратный случай, когда температура электронов намного выше температуры решетки и \(~T_e - T_p \gg T_p - T_c\).
В металлах, как мы уже говорили, средняя скорость хаотического теплового движения электронов практически не зависит от температуры. А вот в полупроводниках увеличение Te под действием электрического поля означает рост скорости υ0 теплового движения электронов, а значит — уменьшение времени свободного пробега. Если изменение Δυ0 скорости υ0 мало, т. е. \(~\Delta \upsilon_0 \ll \upsilon_0\), то зависимостью υ0 от Е и, значит, т от Е можно пренебречь. Условие \(~\Delta \upsilon_0 \ll \upsilon_0\) эквивалентно условию малости перегрева ΔTe электронов относительно равновесного состояния:
Таким образом, условие независимости времени свободного пробега от величины электрического поля, необходимое для выполнения закона Ома, задает следующие ограничения на области применимости этого закона:
Нарушение любого из этих неравенств может привести к отклонению от закона Ома. Ниже мы увидим, что при нарушении неравенств \(~u \ll \upsilon_0\) и \(~\Delta T_e \ll T_e\) электрическое поле Е может влиять и на другие величины, входящие в формулу Друде,— эффективную массу m* и концентрацию электронов n. Зависимости m* и n от Е могут существенно изменить вид вольт-амперных характеристик полупроводников.
Полупроводники в сильном электрическом поле
В образце, по которому течет ток I, выделяется мощность
(мы учли, что \(~I = jS = \sigma ES\), \(~R = \frac{\rho L}{S} = \frac{L}{\sigma S}\)). В единице объема выделяется мощность \(~Q = \sigma E^2\). При одном и том же значении Q электрическое поле \(~E = \sqrt{\frac{Q}{\sigma}}\) в полупроводниках гораздо больше, чем в металлах, так как концентрация электронов в полупроводниках и, значит, проводимость σ намного меньше. Следовательно, в них легче нарушить условия \(~u < \upsilon_{zv}\), \(~u \ll \upsilon_0\). Кроме того, на каждый электрон в полупроводнике приходится большая мощность, чем в металле. Электронный газ разогревается сильнее, поэтому и неравенство \(~\Delta T_e \ll T_e\) тоже нарушается легче.
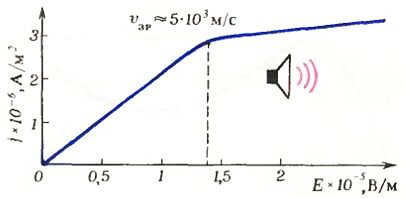
Нарушение какого из условий — (1), (2) или (3) — при увеличении электрического поля приведет к наиболее существенному отклонению от закона Ома, зависит от типа полупроводника. Например, в CdS сначала нарушается условие \(~u < \upsilon_{zv}\). При этом в поле Ezv = 1,4·105 В/м на вольт-амперной характеристике j(E) возникает излом (рис. 2). Если Е > Ezv, этот полупроводник интенсивно испускает звук и может быть использован в качестве генератора звуковых колебаний.
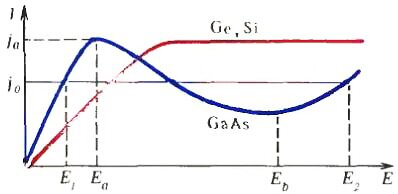
В других полупроводниках, таких как Ge, Si, GaAs, InP, CdTe, звук возбуждается гораздо слабее, и в поле Ezv заметного излома не наблюдается. В этих полупроводниках отклонения от закона Ома связаны с нарушением условия \(~\Delta T_e \ll T_e\). При этом время свободного пробега оказывается обратно пропорциональным полю Е, т. е. \(~\tau (E) \sim \frac 1E\), и зависимость плотности тока от поля связана только с изменением m* и n. В Ge и Si при Е > 106 В/м на вольт-амперной характеристике (рис. 3) наблюдается насыщение j (m*, n не зависят от Е). В GaAs, InP, CdTe при увеличении энергии электронов с ростом Е не только уменьшается время свободного пробега τ, но и растет эффективная масса m*. Увеличение m* вызвано изменением взаимодействия электронов с кристаллической решеткой. В результате в этих полупроводниках, начиная с некоторого значения электрического поля Ea, плотность тока j падает с ростом Е (участок Ea < E < Eb на рисунке 3). В GaAs падение j начинается с Ea = 3,2·105 В/м и продолжается до Eb ≈ 10 Ea. В поле Ea дрейфовая скорость электронов \(~u = \frac{j}{en}\) = 1,5·105 м/с.
В еще более сильном поле Е ~ 107 В/м наряду с нарушением условия \(~\Delta T_e \ll T_e\) нарушается и условие \(~u \ll \upsilon_0\). В таком поле электроны получают за время свободного пробега энергию, достаточную для ионизации атомов. Быстрые электроны при столкновениях с атомами выбивают дополнительные электроны, которые в свою очередь тоже ускоряются полем и генерируют новые носители заряда. Этот процесс называется ударной ионизацией. Общая концентрация n электронов возрастает, и, следовательно, растет проводимость. При еще большем увеличении электрического поля (E > 107 В/м) концентрация и проводимость возрастают лавинообразно, наступает пробой полупроводника.
Таким образом, в полупроводниках в очень сильных полях Е плотность тока \(~j = \sigma E\) увеличивается быстрее, чем по линейному закону. В частности, в Ge и Si насыщение тока сменяется его нелинейным ростом, а в GaAs, InP, CdTe вольт-амперная характеристика приобретает N-образный вид (рис. 3); при 0 < E < Ea выполняется закон Ома, в интервале Ea < E < Eb имеется падающий участок, вызванный уменьшением τ и возрастанием m* в сильном электрическом поле, и, наконец, в области E > Eb происходит быстрый рост j из-за увеличения n.
Эффект Ганна
Наличие падающего участка на вольт-амперной характеристике приводит к интересному явлению, обнаруженному американским инженером Джоном Ганном.
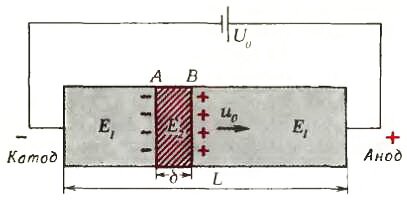
Приложим к образцу GaAs длиной L напряжение U0 такое, чтобы оказаться на падающем участке зависимости j(Е). Предположим, что сначала электрическое поле в образце однородно и равно \(~\frac{U_0}{L}\). Пусть по какой-либо причине в тонком слое АВ образца поле Е оказалось чуть больше, чем в остальном объеме образца (рис. 4). Тогда скорость дрейфа электронов \(~u = \frac{j}{en}\) внутри слоя АВ окажется меньше, чем снаружи. Поэтому к границе А будет подлетать больше электронов, чем улетать от нее, а у границы В — наоборот. Вблизи А возникнет избыток отрицательного заряда, а вблизи В — положительного. Следовательно, в слое АВ появится дополнительное электрическое поле, направленное в ту же сторону, что и исходное. Увеличение поля приведет к тому, что дрейфовая скорость электронов внутри слоя еще уменьшится, и поле там еще больше возрастет.
Таким образом, однородное распределение электрического поля на падающем участке j(Е) невозможно: любая сколь угодно слабая неоднородность Е, случайно возникшая в образце, не рассасывается, а нарастает. В результате образуется узкая область (размером δ) сильного поля, которая называется электрическим доменом. При этом, так как напряжение U0 на образце задано, т. е.
рост поля E2 в домене сопровождается уменьшением поля E1 вне его. Наступит момент, когда E1 < Ea и E2 > Eb (см. рис. 3). Скорость дрейфа электронов вне домена начнет уменьшаться, а внутри — увеличиваться. Рост поля E2 в домене прекратится, когда эти скорости сравняются, и плотности токов в домене и в образце станут одинаковыми:
Из двух последних равенств следует, что установившаяся в образце плотность тока j0 зависит от толщины домена δ.
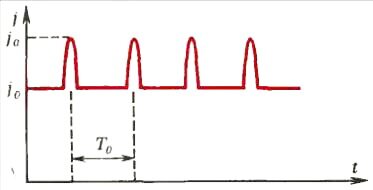
Обычно домен возникает вблизи катода (за счет вплавления контактов здесь больше неоднородностей) и, увлекаемый потоком электронов, начинает двигаться к аноду со скоростью \(~u_0 = \frac{j_0}{en}\). Пока он движется вдоль образца, его размер не меняется, а значит, не меняется и ток j0. Вблизи анода домен начинает исчезать, его толщина уменьшается, и ток в образце возрастает. Одновременно увеличивается поле E1 вне домена. Как только E1 достигнет значения Ea, у катода зарождается новый домен, ток начинает уменьшаться, и этот процесс периодически повторяется (рис. 5). Период колебаний тока в образце — \(~T_0 = \frac{L}{u_0}\).
Итак, прикладывая к полупроводнику постоянное напряжение U0, мы получаем переменный ток частоты \(~f = \frac{1}{T_0} = \frac{u_0}{L}\). Это совсем уж непохоже на закон Ома. В арсениде галлия (GaAs) u0 ≈ 105 м/с. Используя небольшие образцы длиной от одного до ста микрон, можно менять частоту переменного тока в диапазоне f ~ 109 - 1011 Гц. На основе эффекта Ганна работает большинство современных генераторов сверхвысоких частот (СВЧ). Эти приборы используются, например, для определения постами ГАИ скорости движения автомобилей и в телевизионном вещании через искусственные спутники Земли.
Нарушение закона Ома при больших токах
До сих пор мы рассматривали движение электронов под действием только электрического поля. Однако известно, что протекающий по проводнику ток является источником магнитного поля. Магнитное поле возникает не только снаружи, но и внутри проводника. Например, вблизи поверхности прямого провода диаметром d = 1 мм при токе I = 10 А возникает магнитное поле \(~B = \frac{4 \mu_0 I}{d}\) ≈ 0,012 Тл (μ0 = 4·10-7 В·с/(А·м)- магнитная постоянная). Магнитное поле тока тоже может служить причиной нарушения закона Ома.
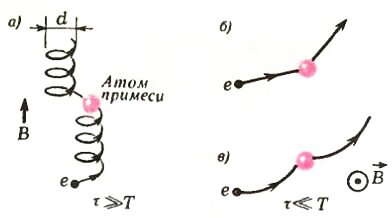
На электрон, движущийся в магнитном поле, действует сила Лоренца, искривляющая его траекторию. Если индукция поля \(~\vec B\) перпендикулярна скорости \(~\vec \upsilon\) электрона, то траекторией электрона будет окружность радиуса \(~r = \frac{m^* \upsilon}{eB}\). Если угол между векторами \(~\vec B\) и \(~\vec \upsilon\) равен α, то электрон будет двигаться по спирали, диаметр которой \(~d = 2 \frac{m^* \upsilon}{eB} \sin \alpha\), пролетая один виток спирали за время \(~T = \frac{2 \pi m^*}{eB}\).
В проводнике движение электрона по спирали возможно, если время свободного пробега \(~\tau \gg T\) (рис. 6, а). При этом диаметр спирали d < υT во много раз меньше расстояния l = υτ, на которое электрон смещается за время τ в отсутствие магнитного поля (рис. 6, б). Поэтому в течение времени τ электрон оказывается как бы запертым в трубке диаметром d. В результате сопротивление проводника в магнитном поле оказывается больше, чем при B = 0. Зависимость сопротивления R от магнитного поля, создаваемого «собственным» током, приводит, таким образом, к нарушению закона Ома.
Если же \(~\tau \ll T\), то между двумя последовательными столкновениями движение электрона мало отличается от прямолинейного (рис. 6, в); магнитное поле практически не меняет сопротивления проводника.
Индукция магнитного поля B0 начиная с которой влияние поля становится существенным, находится из условия равенства периода обращения электрона по круговой орбите \(~T = \frac{2 \pi m^*}{eB_0}\) времени свободного пробега τ\[~B_0 = \frac{2 \pi m^*}{e \tau}\]. Для GaAs m* = 0,06 me и τ ~ 10-13 с, поэтому B0 ≈ 3 Тл. Создать такое поле, пропуская через полупроводник ток, практически невозможно. При гораздо меньших токах образец разрушится. По металлу же, имеющему очень высокую проводимость, можно пропускать намного большие токи. Кроме того, в чистых металлах, охлажденных до температуры жидкого гелия (около 4 К), время τ может достигать величины ~ 10-9 с, значительно большей, чем в полупроводниках. Поэтому в металлах поле B0 мало — порядка 0,01 Тл. Это примерно такое поле, которое возникает в проволоке диаметром 1 мм при токе 10 А.
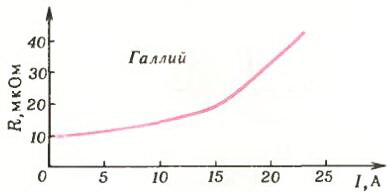
На рисунке 7 приведена полученная экспериментально зависимость сопротивления R металлического проводника от величины тока I при гелиевой температуре. Видно, что с ростом тока сопротивление увеличивается в несколько раз. Электрическое поле в этом эксперименте было меньше 102 В/м, что намного меньше тех полей Е, в которых наблюдаются отклонения от закона Ома в полупроводниках. Таким образом, влияние магнитного поля тока на сопротивление является в данном случае основной причиной нарушения закона Ома.
Мы рассмотрели физические причины, которые могут приводить к нарушению закона Ома в проводниках. При этом не были упомянуты наиболее важные в техническом отношении нелинейные элементы — диоды, транзисторы. Эти элементы специально делают неоднородными, и закон Ома нарушается в местах контакта разных проводящих материалов. Кроме того, мы обошли вниманием многочисленные нелинейные эффекты в проводниках, находящихся в переменных электрическом и магнитном полях... Но ведь «никто не обнимет необъятного».