Kvant. Индукция и принцип относительности
Черноуцан А.И. Электромагнитная индукция и принцип относительности //Квант. — 1987. — № 11. — С. 39-41.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
В 1831 году Фарадей открыл явление электромагнитной индукции. Он обнаружил, что изменение магнитного потока через поверхность, ограниченную замкнутым контуром, приводит к возникновению в нем электрического тока. Опыты Фарадея убедительно доказали, что сила индукционного тока (а значит, и величина ЭДС индукции) совершенно не зависит от того, по какой причине меняется магнитный поток. Можно менять внешнее магнитное поле, оставляя контур неподвижным, — для этого надо либо перемещать источник поля (катушку с током, постоянный магнит), либо менять силу тока в катушке, создающей поле (например, как Фарадей, размыкать и замыкать цепь катушки). «Но можно поступить иначе: не меняя магнитного поля, добиться изменения магнитного потока перемещением самого контура или его деформацией (как, например, в генераторе переменного тока, где ЭДС индукции возникает в проволочной рамке при ее вращении в неизменном магнитном поле). В любом случае индуцированная ЭДС оказывается пропорциональной скорости изменения магнитного потока (закон Фарадея), а направление индукционного тока определяется правилом Ленца («Физика 9», § 92, 93).
Самому Фарадею казалось совершенно естественным, что оба варианта описываются одним и тем же законом. Однако внимательный анализ показывает, что такая ситуация является далеко не очевидной. Попробуем разобраться в этом вопросе поподробнее.
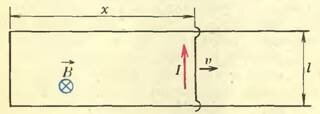
При перемещении контура в магнитном поле, которое не изменяется со временем, роль сторонней силы, порождающей ток в цепи, играет сила Лоренца, которая действует со стороны магнитного поля на любой движущийся заряд. Напомним известный вам пример («Физика 9», § 95). Пусть в однородное магнитное поле с индукцией \(~\vec B\) помещен прямоугольный контур, плоскость которого перпендикулярна линиям индукции (рис. 1).
Одна из сторон контура представляет собой перемычку со скользящими контактами. Если перемещать перемычку со скоростью υ, то в ней возникнет ЭДС индукции \(~\varepsilon = B \upsilon l\) (l — длина перемычки). Действительно, на свободный заряд q в движущейся перемычке действует сила Лоренца \(~F = q \upsilon B\) (направление силы указано стрелкой); соответствующая этой сторонней силе ЭДС
где А — работа сторонней силы на длине перемычки. Сравним этот результат со скоростью изменения магнитного потока:
Легко также проверить, что знак возникшей ЭДС соответствует правилу Ленца.
Разобранный пример показывает, что в случае движения проводников в постоянном магнитном поле возникновение индукционного тока не представляет собой принципиально нового физического явления.
Совсем другая картина получается в случае неподвижного контура, помещенного в изменяющееся со временем магнитное поле. Так как свободные заряды в проводнике изначально неподвижны (разумеется, хаотичное тепловое движение мы не учитываем), магнитное поле на них не действует и поэтому не может вызвать их направленного перемещения. Следовательно, индукционный ток может появиться только под действием электрического поля. Как оно возникает и какими свойствами обладает?
Ясно, что во многом это электрическое поле отличается от известного электростатического поля. Например, оно создает ЭДС в замкнутом контуре, значит, его работа по перемещению зарядов по замкнутому пути не равна нулю. Это поле вихревое, т. е. его силовые линии имеют вид замкнутых линий. И т. д.
Мы видим, что анализ ситуации, возникающей в случае неподвижного контура в переменном магнитном поле, приводит к широкому кругу совершенно новых физических явлений, указывающих на прямую взаимосвязь электрического и магнитного полей. Так Максвелл в 1860 году пришел к выводу, что переменное во времени магнитное поле всегда порождает вихревое электрическое поле. Далее, следуя внутреннему ощущению симметрии физических законов, он постулирует факт, не подкрепленный в то время никакими экспериментами: переменное во времени электрическое поле всегда, в свою очередь, порождает магнитное поле. Придав этим физическим утверждениям математически симметричную форму (уравнения Максвелла), он завершил построение единой теории электромагнитного поля.
После всех этих рассуждений может показаться, что закон электромагнитной индукции описывает два совершенно разных физических явления. В постоянном магнитном поле индукционный ток в движущемся контуре вызывается самим магнитным полем, а изменяющееся магнитное поле порождает вихревое электрическое поле, которое и заставляет заряды двигаться вдоль неподвижного контура. Так почему же закон электромагнитной индукции для этих случаев один и тот же? Что это — удивительное совпадение? Оказывается, в этом «совпадении» проявляется глубокая связь теории электромагнитного поля со специальной теорией относительности, в основе которой лежит принцип относительности Эйнштейна. (Основные идеи специальной теории относительности были сформулированы Эйнштейном в 1905 году). Согласно этому принципу все явления природы (не только законы механики, как это следует из принципа относительности Галилея) должны происходить одинаково во всех инерциальных системах отсчета. Важное следствие этого принципа заключается, в частности, в том, что нельзя однозначно, вне зависимости от системы отсчета, сказать, какие поля существуют в окружающем пространстве.
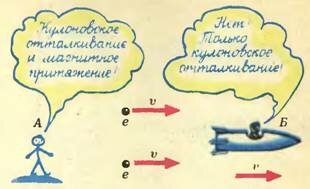
Рассмотрим в качестве примера взаимодействие двух электронов с точки зрения двух наблюдателей (рис. 2). Наблюдатель А утверждает, что движущиеся заряды создают вокруг себя как электрическое, так и магнитное поле, и кроме кулоновского отталкивания между ними действует магнитное притяжение (как между параллельными токами). Наблюдатель Б не согласен с ним и утверждает, что магнитного поля нет, раз заряды покоятся, и между электронами действует только кулоновское отталкивание. Принцип же относительности примиряет обоих наблюдателей, утверждая, что оба они правы, поскольку понятия электрического и магнитного полей являются относительными, зависящими от системы отсчета. Оба эти поля выступают как части единого целого — электромагнитного поля.
Вернемся, однако, к закону Фарадея и представим себе следующий мысленный эксперимент. Будем сближать постоянный магнит и замкнутый проводящий контур (рис. 3). Гальванометр, включенный в контур, зафиксирует индукционный ток. Отклонение стрелки гальванометра увидят как наблюдатель А, который стоит на магните, так и наблюдатель Б, сидящий на контуре. «Все ясно, — скажет наблюдатель А, — контур движется в постоянном поле моего магнита, на заряды в контуре действует сила Лоренца — вот и течет ток!». Наблюдатель Б скажет иное: «Магнит приближается к моему неподвижному контуру. Изменяющееся магнитное поле порождает вихревое электрическое поле — оно и создает ток в контуре!». Но, по Эйнштейну, оба наблюдателя правы. Оба они видят одно и то же отклонение стрелки гальванометра, т. е. один и тот же результат проявления закона Фарадея. А это означает, что и сам закон Фарадея, конечно же, должен быть одинаковым для обоих рассмотренных случаев.