Kvant. Интерференция волн

Баканина Л.П. Интерференция волн //Квант. — 1983. — № 5. — С. 34-37.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Интерференция волн — большой и важный раздел физики. Исследование этого явления сыграло большую роль в развитии оптики, так как обнаружение интерференции света служит убедительным доказательством его волновой природы.

При наложении волн действует принцип суперпозиции — результирующее колебание представляет собой сумму колебаний, вызванных каждой волной в отдельности. Однако интерференционная картина возникает только тогда, когда складывающиеся колебания (а значит, и вызывающие их волны) когерентны, то есть они имеют одинаковые частоты и постоянную во времени разность фаз. Что же представляет собой эта картина?

Пусть вдоль некоторого направления распространяется плоская синусоидальная волна. В точке, находящейся на расстоянии d, она вызовет колебания, происходящие по закону

\(~a = A \cos \omega \left( t - \frac{d}{\upsilon} \right) = A \cos \left(\omega t - \frac{2 \pi}{T}\frac{d}{\upsilon} \right) = A \cos \left(\omega t - \frac{2 \pi}{\lambda}d \right)\) .

Здесь a — значение колеблющейся величины в момент времени t, A — амплитуда, ω — циклическая частота, \(~T = \frac{2 \pi}{\omega}\) — период колебаний, υ — скорость волны (для электромагнитных волн υ равно скорости света c).

При сложении двух когерентных волн одинаковой амплитуды получаем

\(~a = a_1 + a_2 = A \cos \left(\omega t - \frac{2 \pi}{\lambda}d_1 \right) + A \cos \left(\omega t - \frac{2 \pi}{\lambda}d_2 \right) = 2A \cos \left(\frac{2 \pi}{\lambda} \frac{d_2 - d_1}{2} \right) \cos \left(\omega t - \frac{2 \pi}{\lambda} \frac{d_1 + d_2}{2} \right)\) .

Амплитуда результирующего колебания равна

\(~A_{res} = 2A \left|\cos \frac{2 \pi}{\lambda} \frac{d_2 - d_1}{2} \right| = 2A \left|\cos \frac{\Delta \varphi}{2} \right|\) .

где \(~\Delta \varphi = s \pi \frac{d_2 - d_1}{\lambda}\) — разность фаз складываемых колебаний. В зависимости от разности фаз Δφ, а значит и от разности хода (d₂ — d₁) волн, результирующая амплитуда может меняться от A_{res max} = 2А (когда фазы совпадают) до A_{res min} = 0 (когда фазы сдвинуты на π).

Глаз (или фотоприемник) воспринимает не амплитуду колебаний, а их интенсивность I, то есть энергию, падающую в единицу времени на единицу площади. Интенсивность, как и энергия колебаний, пропорциональна квадрату амплитуды, поэтому

\(~I_{res} \sim A^2_{res} \sim 4A^2 \cos^2 \frac{\Delta \varphi}{2}\) .

Следовательно, есть точки, где суммарная интенсивность больше суммы интенсивностей налагающихся волн (I_{res max} ~ 4A²), и точки, где волны как бы уничтожают друг друга (I_{res min} = 0). Такое перераспределение энергии в пространстве и является характерным признаком интерференции.

Явление интерференции легко демонстрируется для волн на воде или для радиоволн. В оптике наблюдать интерференционную картину нелегко, так как обычные источники света (не лазеры) испускают колебания с быстро и случайно изменяющейся фазой и, следовательно, некогерентные. Однако если свет от одного источника разделить на два пучка и затем наложить эти пучки друг на друга, то можно получить достаточно четкую интерференционную картину.

Заметим, что для правильного описания явления интерференции ошибка при определении разности фаз колебаний должна быть существенно меньше π (иначе будет невозможно отличить максимум от минимума). При этом ошибка в измерении разности хода волн должна быть много меньше длины волны λ (для световых волн эта ошибка должна быть много меньше 0,1 мкм).

Теперь разберем несколько конкретных задач. Почти все они взяты из билетов письменного экзамена по физике в Московский физико- технический институт.

Задача 1

Плоская электромагнитная волна частоты ν, сформированная рупорной антенной, падает перпендикулярно на плоский отражающий экран. Определите амплитуду отраженной волны, если измеритель напряженности электрического поля при перемещении между экраном и рупором зафиксировал максимальную амплитуду поля A₁ и минимальную A₂. Определите также расстояние между двумя соседними максимумами поля.

В пространстве между рупором и отражающим экраном происходит наложение падающей и отраженной волн. В точках максимума фазы колебаний, вызванных этими волнами, совпадают, и, следовательно, результирующее колебание происходит с амплитудой

\(~A_1 = A_{pad} + A_{otr}\) .

В точках минимума падающая и отраженная волны находятся в противофазе, и суммарная амплитуда колебаний равна

\(~A_2 = A_{pad} - A_{otr}\) .

Из этих двух равенств находим

\(~A_{otr} = \frac{A_1 - A_2}{2}\) .

Пусть колебания в точке с координатой х, вызванные падающей волной, описываются выражением

\(~a_{pad} = A_{pad} \cos \omega \left( t - \frac{x}{c} \right) = A_{pad} \cos \left(\omega t - \frac{2 \pi}{\lambda}x \right)\) .

Если расстояние от рупора до экрана равно l, то отраженная волна проходит до данной точки расстояние 2l — х, и колебания, вызванные отраженной волной, имеют вид

\(~a_{otr} = A_{otr} \cos \omega \left( t - \frac{2l - x}{c} \right) = A_{otr} \cos \left(\omega t + \frac{2 \pi}{\lambda}x - \frac{4 \pi}{\lambda} l \right)\) .

(На самом деле при отражении волны фаза колебаний может измениться на противоположную, но на дальнейшие наши рассуждения это повлиять не может.)

Пусть два соседних максимума наблюдаются в точках с координатами x₁ и x₂. Разности фаз колебаний, возбуждаемых падающей и отраженной волнами в этих точках, равны соответственно

\(~(\Delta \varphi)_1 = \left(\omega t - \frac{2 \pi}{\lambda}x_1 \right) - \left(\omega t + \frac{2 \pi}{\lambda}x_1 - \frac{4 \pi}{\lambda} l \right) = - \frac{4 \pi}{\lambda} x_1 + \frac{4 \pi}{\lambda} l\)

и

\(~(\Delta \varphi)_2 = - \frac{4 \pi}{\lambda} x_2 + \frac{4 \pi}{\lambda} l\) .

В двух соседних максимумах фазы результирующих колебаний должны отличаться на 2π; следовательно,

\(~\Delta \varphi = (\Delta \varphi)_1 - (\Delta \varphi)_2 = 2 \pi\) ,

или

\(~\frac{4 \pi}{\lambda} (x_2 - x_1) = 2\pi\) .

Отсюда получаем

\(~x_2 - x_1 = \frac{\lambda}{2} = \frac{c}{2 \nu}\) .

Задача 2

Рис. 1

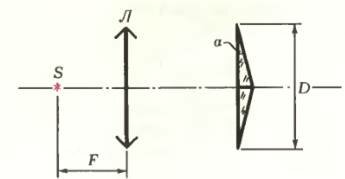
Точечный источник света S расположен в фокусе линзы Л, за которой находится бипризма с преломляющим углом α = 0,01 рад и шириной D = 6 см (рис. 1). На каком расстоянии L от бипризмы можно наблюдать наибольшее число интерференционных полос? Сколько полос можно увидеть на экране? Чему равна ширина полос? Коэффициент преломления стекла бипризмы n = 1,5, длина волны света λ = 0,5 мкм.

Рис. 2

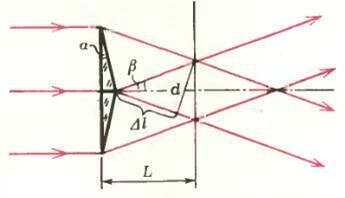
Поскольку источник света находится в фокусе линзы, на бипризму падает параллельный пучок, идущий вдоль оптической оси системы (рис. 2). Из бипризмы выходят два параллельных световых пучка, наклоненных к оси под углом β, который можно найти из закона преломления \(~\frac{\sin \alpha}{\sin \beta} = n\). Так как углы малы,

\(~\beta \approx \sin \beta = \frac{\sin \alpha}{n} \approx \frac{\alpha}{n}\) .

Очевидно, что наибольшая ширина интерференционной картины будет в том месте, где самая большая площадь пересечения интерферирующих пучков. Из рисунка 2 видно, что это будет на расстоянии

\(~L \approx \frac{D}{4 \operatorname{tg} \beta} \approx \frac{D}{4 \beta} \approx \frac{Dn}{4 \alpha}\) ≈ 112,5 см.

При этом ширина всей интерференционной картины равна b = D/2 = 3 см.

Каждый из пересекающихся пучков имеет ширину \(~d = \frac D2 \cos \beta \approx \frac D2\). Волновые поверхности пучков образуют между собой угол, равный 2β; следовательно, максимальная разность хода пучков равна

\(~\Delta l = d \operatorname{tg} 2\beta \approx d \cdot 2\beta \) .

Разность ходя, соответствующая двум соседним максимумам (или минимумам), равна длине волны λ. Таким образом, число интерференционных полос, образующихся на экране, равно

\(~N = \frac{\Delta l}{\lambda} \approx \frac{2d \beta}{\lambda} \approx \frac{D \alpha}{n \lambda} \approx 800\) .

а ширина одной полосы —

\(~b_0 = \frac bN \approx \frac{\frac D2 \alpha}{\frac{D \alpha}{n \lambda}} \approx \frac{n \lambda}{2 \alpha}\) ≈ 37,5 мкм.

Задача 3

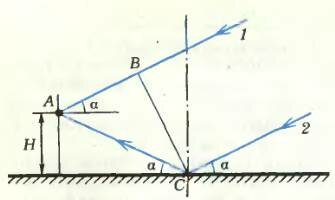
Приемник радиосигналов, следящий за появлением спутника Земли из-за горизонта, расположен на берегу озера на высоте Н = 3 м над поверхностью воды. По мере поднятия спутника над горизонтом наблюдаются периодические изменения интенсивности принимаемого сигнала. Определите частоту радиосигнала спутника, если максимумы интенсивности наблюдались, в частности, при углах возвышения спутника над горизонтом α₁ = 3° и α₂ = 6°. Поверхность озера можно считать идеально отражающим зеркалом.

Рис. 3

В приемник попадают лучи, идущие непосредственно от спутника и отразившиеся от поверхности озера. На рисунке 3 это лучи 1 и 2 соответственно. Разность хода между ними

\(~\Delta l = |AC| - |AB| = \frac {H}{\sin \alpha} - \frac {H}{\sin \alpha} \cos 2 \alpha\)

(ВС — волновая поверхность, перпендикулярная обоим лучам). Рассматриваемые в задаче углы малы, так что \(~\sin \alpha \approx \alpha\) и \(~\cos \alpha \approx 1 - \frac{\alpha^2}{2}\), откуда получаем

\(~\Delta l = \frac {H(1 - \cos 2 \alpha)}{\sin \alpha} \approx 2H \alpha\) .

Максимум интенсивности принимаемого сигнала наблюдается, если разность хода интерферирующих лучей равна целому числу длин волн:

\(~2H \alpha_1 = k \lambda\) и \(~2H \alpha_2 = (k + 1)\lambda\).

Отсюда длина волны равна

\(~\lambda = 2H (\alpha_2 - \alpha_1) \) ,

а частота радиосигнала —

\(~\nu = \frac{c}{\lambda} = \frac{c}{2H (\alpha_2 - \alpha_1)} \) ≈ 10⁹ Гц.