Kvant. Как зависит g от глубины
Позвоните до 14:00, и мастер компании "Копи-Групп" выедет к вам сегодня!
Черноуцан А. И. Как зависит g от глубины? //Квант. — 1990. — № 3. — С. 49-52.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Вопрос: Что это — большое, зеленое, живет на глубине трех метров под землей и ест камни? Ответ: Большой Зеленый Камнеед.
Из фольклора МФТИ
Как будет изменяться сила тяготения по мере погружения тела в воображаемую шахту, прорытую сквозь Землю по ее диаметру? Какая сила тяготения действовала бы внутри некоторой «полой» планеты? Можно ли было бы ходить по ее внутренней поверхности? Попытаемся ответить на эти и аналогичные им вопросы. И не для того, конечно, чтобы выработать инструкцию для бурильщиков сверхглубоких скважин или для астронавтов, а чтобы лучше разобраться в законе всемирного тяготения.
Закон всемирного тяготения, открытый Ньютоном, утверждает, что любые две материальные частицы (точечные массы) притягиваются друг к другу с силой, пропорциональной массам этих частиц m1 и m2 и обратно пропорциональной квадрату расстояния r между ними:
где G = 6,67•10-11 Н•м2/кг2 — гравитационная постоянная. В произвольном случае неточечных масс для определения силы тяготения можно воспользоваться широко известным в физике принципом суперпозиции.
Пусть, например, нам нужно рассчитать силу тяготения, действующую на точечную массу m со стороны тела произвольной формы. Мысленно разобьем тело на точечные массы m1, m2, …, mn, вычислим силы, действующие на массу m со стороны всех точечных масс, а затем векторно сложим эти силы. Что же получится в итоге? Сразу бросаются в глаза два факта. Во-первых, сила, действующая на точечную массу m, пропорциональна величине этой массы. Во-вторых, сила существенно зависит от того, какое именно тело взаимодействует с нашей точечной массой — какова его форма и размеры, какой массой оно обладает.
Кто и как действует на массу m в нашем примере? Непосредственно массы m1, …, mn через пустое пространство, их разделяющее? Или существует некоторый «посредник»? По современным представлениям таким материальным посредником является поле тяготения, создаваемое массами m1, …, mn во всем окружающем пространстве. Именно это поле и действует на массу m, в нем находящуюся. Если, например, изменить какую-нибудь из масс или как-то сместить их, то изменится и поле.
Для количественной характеристики поля тяготения в данной точке вводится специальная физическая величина — напряженность гравитационного поля. Определим ее так. Запишем выражение для силы тяготения, действующей на точечную массу m, в виде
где \(~\vec g\) (величина, не зависящая от m) и есть напряженность гравитационного поля. Она имеет простой физический смысл: с таким ускорением будет двигаться любая точечная масса, если ее поместить в данную точку поля и освободить. В частном случае, когда точечная масса взаимодействует с Землей, \(~\vec g\) — это известное вам ускорение свободного падения.
От чего и как зависит \(~\vec g\)? Как и сила тяготения, напряженность поля подчиняется принципу суперпозиции :
где \(~\vec g_1, \ldots , \vec g_n\) — напряженности полей, создаваемых в данной точке пространства отдельными массами m1, …, mn. Из выражений (1) и (2) следует, что любая точечная масса М создает вокруг себя поле, напряженность которого направлена к этой точке и зависит от расстояния r до нее по закону
А какое гравитационное поле создает вокруг себя сферически симметричное тело? Ответ на этот вопрос был известен Ньютону с самого начала — сила притяжения к Земле вычисляется по той же формуле (1), где r — расстояние до центра Земли. Однако Ньютон понимал, что такое утверждение требует доказательства. Потратив очень много времени и сил, он доказал, что сила притяжения к тонкой сфере тел, расположенных вне нее, равна силе притяжения к материальной точке той же массы, расположенной в центре сферы. А поскольку шар можно разбить на тонкие сферы, такой же результат остается в силе и для шара. Переходя на язык поля, скажем, что величина напряженности поля тяготения, создаваемого тонкой сферой (или шаром) радиусом R, на расстоянии r > R от центра задается формулой (3).
Доказательство по принципу суперпозиции является действительно достаточно сложным. Однако его можно обойти. Как это сделать, показано в следующей заметке — «Силовые линии и теорема Гаусса» на примере электрического поля. Попробуйте прочитать эту заметку, всякий раз заменяя слово «заряд» словом «масса», а слова «электрическое поле» словами «поле тяготения». Если вам будет трудно разобраться в деталях, постарайтесь понять хотя бы общий смысл.
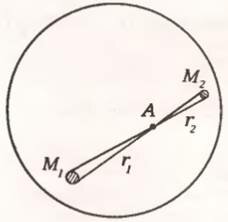
Выясним теперь, каково поле тяготения внутри тонкой сферы, т. е. при r < R. Оказывается, внутри сферы напряженность поля равна нулю. Для доказательства возьмем произвольную точку, например точку А на рисунке 1, и покажем, что вклады в \(~\vec g_A\) от двух противоположных участков поверхности сферы, отсекаемых узким конусом, взаимно уничтожаются. Действительно, из подобия следует, что линейные размеры выбранных участков относятся как \(~\frac{r_1}{r_2}\), следовательно, отношение их площадей \(~\frac{S_1}{S_2}\), равное отношению масс \(~\frac{M_1}{M_2}\), есть \(~\frac{r^2_1}{r^2_2}\). Тогда из формулы (3) получаем, что создаваемые этими участками в точке А напряженности равны по величине. А поскольку направления их противоположны, они в сумме дают ноль.
Интересный результат, не правда ли? Если бы внутри Земли, скажем, существовала концентрическая пустая полость (как, например, в случае, описанном в научно-фантастическом романе В. А. Обручева «Плутония. Необычайное путешествие в недра земли»), то в этой полости была бы полная невесомость. Оттолкнись чуть-чуть от поверхности и полетишь равномерно и прямолинейно до противоположной стенки. Так что путешествовать по такой Плутонии крайне затруднительно.
Теперь мы можем ответить и на самый первый вопрос — чему равно поле тяготения в шахте, прорытой вдоль диаметра Земли. Для простоты будем считать Землю однородным шаром с радиусом R. Рассмотрим точку на расстоянии r < R от центра Земли. Проведя мысленно сферу радиусом r, разделим Землю на две части — внешнюю и внутреннюю. Как мы уже выяснили, поле, создаваемое в рассматриваемой точке всеми внешними сферическими слоями, равно нулю. Поэтому поле Земли в данной точке совпадает с полем, созданным внутренней частью, т. е. шаром радиусом r. Чтобы использовать формулу (3), надо найти массу Mr этого шара. Очевидно, что отношение массы Mr к массе Mz, всей Земли равно отношению их объемов, т. е. отношению кубов радиусов\[~\frac{M_r}{M_z} = \frac{r^3}{R^3}\]. Следовательно,
где g0 — ускорение свободного падения на поверхности Земли.
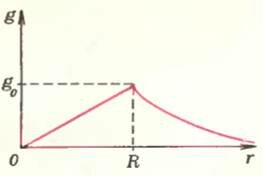
Итак, мы знаем gr на любых расстояниях от центра Земли, как при r > R, так и при r < R. Эта зависимость изображена графически на рисунке 2. Попробуем использовать полученные результаты для ответа на вопрос, который любили задавать абитуриентам МФТИ в самом конце собеседования: «Что будет с камнем, брошенным в прорытый сквозь Землю колодец?» Ответить на этот вопрос совсем просто, если вы знакомы со свойствами гармонических колебаний. Действительно, раз сила притяжения пропорциональна r, тело будет совершать колебания относительно центра Земли (сопротивление воздуха, естественно, при этом не учитывается). Интересно, что такие же колебания (с таким же периодом) будет совершать и тело в колодце, прорытом наклонно. Существовали даже фантастические проекты межконтинентального пассажирского сообщения по прорытым каналам с помощью вагонов на воздушной подушке (подробнее об этом можно прочитать в книге Я. И. Перельмана «Занимательная физика»).
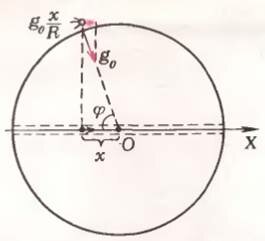
Оказывается, даже не зная ничего о колебаниях, все же можно понять, как будет двигаться камень, брошенный в прорытый колодец. Сравним между собой два движения — камня в колодце и спутника, летящего по околоземной круговой орбите. Точнее, проекции спутника на ось X, проведенную сквозь колодец (рис. 3). Легко убедиться, что проекция ускорения спутника равна \(~a_x = g_0 \cos \varphi = g_0 \frac{x}{R}\). Но именно с таким ускорением будет двигаться камень на расстоянии x от центра (см. выражение (4)). Значит, и время движения камня сквозь Землю и обратно совпадает с периодом обращения спутника вокруг Земли. Кроме того, легко определить максимальную скорость камня. Очевидно, что она будет равна скорости спутника, т. е. первой космической скорости \(~\upsilon_1 = \sqrt{g_0 R}\) ≈ 8 км/с.
А теперь представьте себе выражение лица несчастного абитуриента, когда, изложив все эти тонкие физические соображения, он вдруг слышит в ответ: «Как же так, молодой человек? Такая невнимательность! Вы что, забыли? Камень пролетит в колодце всего три метра, после чего его съест Большой Зеленый Камнеед!»