Kvant. Космические скорости

Туров В. По ступеням космических скоростей //Квант. — 1992. — № 4. — С. 56-58.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Бывают даже такие дети (я их встречал),
которым хочется знать, как выглядит черная дыра...
К. Саган

Мы живем на дне глубокого гравитационного «колодца». Изучением этого дна — поверхности Земного шара — заполнена вся история человечества. Но всегда находились отчаянные мечтатели — легенда об Икаре тому свидетельство,— которым хотелось шагнуть не за горизонт, а — ввысь. Трудами многочисленных ученых, начиная с безвестных халдейских звездочетов, через Птолемея и Коперника, Галилея и Кеплера, и, наконец, великого Ньютона, люди пришли к пониманию закономерностей движения в поле сил тяжести.

А. Штернфельд, один из пионеров космонавтики, размышляя о возможности полета в космическом пространстве, ввел, независимо от К. Э. Циолковского, понятие первой космической скорости и предложил ее «в качестве единицы для сравнения космических скоростей, характеризующих данную планету». Далее он выстроил целую систему космических скоростей — своеобразную космическую лестницу. Давайте пройдем по нескольким ступеням этой лестницы.

Предварительно получим простое, но очень важное соотношение для потенциальной энергии тела в центрально-симметричном гравитационном поле, т. е. таком поле, в котором величина силы тяжести зависит только от расстояния до центра тяготения. Именно таким является поле всех космических тел, которые приближенно можно считать сферическими,— планет, звезд и т. п.

Элементарная работа перемещения тела массой m в поле тяготения небесного тела массой М равна

\(~dA = Fdr = -G \frac{Mm}{r^2} dr,\)

где r — расстояние между центрами масс обоих тел, G — гравитационная постоянная. Изменение потенциальной энергии тела, когда его расстояние до центра тяготения меняется от r₁ до r₂, равно работе, совершаемой над телом при таком перемещении:

\(~\Delta E_p = -\int^{r_2}_{r_1} dA = GMm \left( \frac{1}{r_1} - \frac{1}{r_2} \right).\)

Подсчитаем минимальную энергию, требующуюся для выведения космического корабля на круговую орбиту радиусом r с поверхности планеты радиусом r₀. В этом случае нам необходимо не только изменить потенциальную энергию корабля в поле тяготения, но и сообщить ему некоторую кинетическую энергию для обращения по круговой орбите. Скорость обращения находится из условия равенства ускорения свободного падения и центростремительного ускорения:

\(~\frac{GM}{r^2} = \frac{\upsilon^2_{kr}}{r}\)

и составляет

\(~\upsilon_{kr} (r) = \sqrt{\frac{GM}{r}}.\)

Тогда минимальная кинетическая энергия, которую должны сообщить кораблю двигатели при взлете, равна

\(~\frac{\upsilon^2_v}{2} = \frac{\upsilon^2_{kr}}{2} + \Delta E_p = GMm \left( \frac{1}{r_0} - \frac{1}{2r} \right),\)

откуда находим взлетную скорость, позволяющую вывести корабль на круговую орбиту радиусом r:

\(~\upsilon_v (r) = \sqrt{GM \left( \frac{2}{r_0} - \frac{1}{r} \right)}.\)

Возьмем вначале радиус орбиты r = r₀. Тогда

\(~\upsilon_v (r_0) = \sqrt{\frac{GM}{r_0}} = \upsilon_1,\)

где υ₁ — первая космическая скорость для рассматриваемой планеты.

Для Земли, которая естественно интересует нас прежде всего, υ_1z = 7,9 км/с.

Пусть теперь \(~r \to \infty\), т. е. корабль, стартуя с поверхности планеты, имеет такую скорость, что способен преодолеть узы тяготения планеты и удалиться от нее на произвольно большое расстояние. При этом корабль будет двигаться по параболической траектории. По этой причине такая скорость носит название параболической относительно данной планеты, или второй космической. Она равна

\(~\upsilon_v (\infty) = \upsilon_{par} = \sqrt{\frac{2GM}{r_0}} = \sqrt 2 \upsilon_1 = \upsilon_2.\)

Для Земли υ_2z = 11,2 км/с.

Все эти рассуждения справедливы для изолированной планеты. Однако, если планета входит в планетную систему, имеющую центральное светило — Солнце, то, освободившись от тяготения планеты, корабль отнюдь не избавится от притяжения Солнца. Теперь он станет обращаться по замкнутой траектории вокруг Солнца.

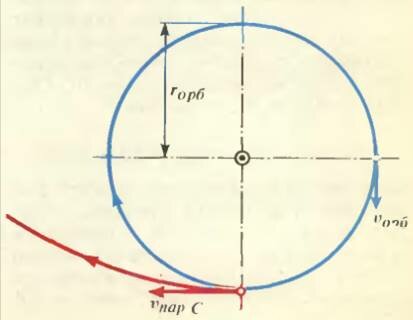
Чтобы разорвать путы солнечного притяжения, мы должны сообщить кораблю параболическую скорость относительно Солнца (см. рисунок):

\(~\upsilon_{par\ C} = \sqrt{\frac{2GM_C}{r_{orb}}} = \sqrt 2 \upsilon_{orb},\)

где M_C — масса Солнца, r_orb — радиус орбиты планеты, которую мы для простоты считаем круговой, υ_orb — скорость орбитального движения планеты.

Для Земли υ_orb = 29,8 км/с и υ_{par C} = 42,1 км/с.

Означает ли это, что мы обязаны разогнать корабль до скорости 42,1 км/с для того, чтобы он ушел произвольно далеко от Солнца? Конечно, нет, ведь мы можем использовать грандиозную катапульту, которой снабдила нас природа,— Землю, несущуюся по своей орбите со скоростью υ_orb. Легко понять, что для Земли скорость, позволяющая, хотя бы в принципе, долететь до любого космического объекта, расположенного в плоскости орбиты Земли за пределами Солнечной системы,— третья космическая скорость — равна

\(~\upsilon_3 = \sqrt{\upsilon^2_2 + (\upsilon_{par\ C} - \upsilon_{orb})^2}\) = 16,7 км/с.

Итак, сообщив кораблю скорость υ₃ у поверхности Земли, мы можем послать его к любой звезде, лежащей в плоскости обращения Земли. К любой, кроме ближайшей — Солнца! Это — один из парадоксов, отмеченных А. Штернфельдом.

Можно показать, что для того, чтобы корабль мог двигаться по направлению к центру Солнца, нужно полностью компенсировать орбитальное движение Земли. Тем самым, четвертая космическая скорость относительно Земли равна

\(~\upsilon_4 = \sqrt{\upsilon^2_2 + \upsilon^2_{orb}}\) = 31,8 км/с.

Далее, следуя Штернфельду, можно ввести понятия пятой и шестой космических скоростей. Пятая позволяет достичь любого космического объекта, двигаясь в плоскости, перпендикулярной к плоскости орбиты Земли. Она определяется выражением

\(~\upsilon_5 = \sqrt{\upsilon^2_2 + \upsilon^2_{orb} + \upsilon^2_{par\ C}}\) = 52,8 км/с.

При шестой космической скорости так же, как и в случае третьей, полет происходит по параболе в плоскости орбиты Земли, но стартовать можно против направления орбитального движения, что позволяет лететь к избранному космическому объекту в произвольный момент времени. Эта скорость равна

\(~\upsilon_6 = \sqrt{\upsilon^2_2 + (\upsilon_{orb} + \upsilon_{par\ C})^2}\) = 72,8 км/с.

А. Штернфельд считал, что эти скорости могут быть полезны при изучении комет.

И наконец, вернемся еще раз к выражению для параболической скорости относительно какого-либо гравитирующего тела сферической формы

\(~\upsilon_{par} = \sqrt{\frac{2GM}{R}}.\)

Как мы видим, величина этой скорости зависит от массы тела М и от его радиуса R, причем с уменьшением радиуса скорость увеличивается. В ньютоновской механике нет никаких ограничений для величины скорости, однако мы знаем, что такие ограничения возникают в специальной теории относительности: никакой материальный объект не может иметь скорость, большую скорости света в вакууме с = 3·10⁵ км/с.

Для гравитирующего тела можно поставить вопрос: какой радиус должно иметь это тело для того, чтобы никакой материальный объект не мог удалиться от него на произвольно большое расстояние? Такой радиус называется гравитационным радиусом данного тела и определяется выражением

\(~R_{gr} = \frac{2GM}{c^2}.\)

Попробуйте самостоятельно посчитать гравитационный радиус для Земли и оценить, какой при этом стала 'бы плотность земного вещества.

Оказывается, если по тем или иным причинам размер какого-либо тела становится меньше гравитационного радиуса, тело превращается в черную дыру. Тем читателям, кому захочется узнать побольше о свойствах этих образований, рекомендую прочитать прекрасную книгу выдающегося английского ученого С. Хокинга «От большого взрыва до черных дыр», вышедшую в издательстве «Мир» в 1990 году. Из предисловия к этой книге американского астрофизика К. Сагана и взят наш эпиграф.