Kvant. Микроскоп
Варламов А.А. На что способен микроскоп? //Квант. — 1985. — № 1. — С. 27-29.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
При создании оптических приборов, «вооружающих» глаз, естественно возникает вопрос об их предельных возможностях. Для микроскопа, например, такой характеристикой служит его увеличение. С точки зрения геометрической оптики, подбирая соответствующие окуляр и объектив, увеличение микроскопа можно сделать сколь угодно большим. Однако в действительности это не так, и причина тому — волновая природа света. Представление о лучах света как о геометрических линиях служит лишь приближением, справедливым до тех пор, пока длина волны света много меньше размеров исследуемого предмета.
Прежде чем говорить о «способностях» микроскопа, рассмотрим некоторую механическую задачу. Не будучи буквальной аналогией, она все же поможет понять, где лежат пределы возможностей оптических приборов.
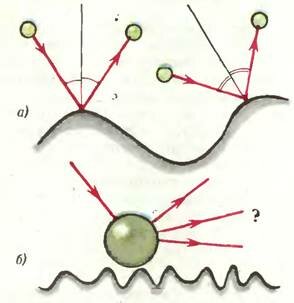
Представьте себе, что некий исследователь решил изучать форму упругой холмистой поверхности. Для этого, в частности, ему понадобилось уметь восстанавливать перпендикуляр к поверхности в любой ее точке. К этой задаче исследователь подошел несколько необычным способом — он стал бросать на поверхность упругий шарик, измеряя каждый раз угол между направлениями падения и отражения шарика и строя биссектрису этого угла. Очевидно, что таким способом действительно можно получить необходимый набор перпендикуляров, но только в том случае, если диаметр шарика много меньше расстояний между ближайшими «горбами» и радиусами их кривизны (рис. 1, а). В противном случае (рис. 1, б) никакой информации о форме поверхности получить не удастся.
Нечто подобное происходит и при наблюдении за объектом в микроскоп, хотя между световыми лучами и шариками имеется существенное различие. По мере того как мы хотим рассматривать все более и более мелкие детали объекта, мы изменяем увеличение микроскопа. Оказывается, при увеличении примерно в 2000 раз можно различить две точки, если они находятся друг от друга на расстоянии порядка 0,2 мкм, что составляет около половины длины волны для видимого света. Формально можно довести увеличение микроскопа и до 5000, и до 10 000, однако при этом точки, находящиеся на расстояниях, меньше 0,2 мкм, останутся неразличимыми.
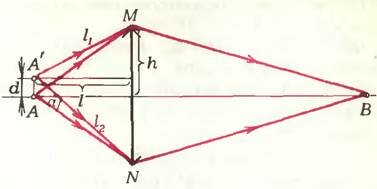
Попробуем разобраться, почему так происходит, обратившись к волновым свойствам света. Рассмотрим тонкую линзу (которая может служить объективом нашего микроскопа). Пусть изображение некоторой точки А находится в точке В (рис. 2). Возьмем точку А’, близкую к точке А. Из геометрической оптики следует, что ее изображение будет находиться в некоторой точке В’, заведомо не совпадающей с точкой В. Однако всегда ли наблюдателю удается различить точки В и В’, то есть увидеть их именно как две точки?
С точки зрения волновой оптики изображение в линзе каждой точки формируется совокупностью всех лучей, проходящих через линзу. В нашем примере это означает, что изображение точки А’ не совпадет с точкой В в том случае, если времена прохождения через линзу крайних лучей А’МВ и A’NB будут различными. А что под этим подразумевается? Тут следует заметить, что времена можно считать различными, если они отличаются друг от друга хотя бы на период Т колебаний световой волны. В рассматриваемой задаче это единственный имеющийся в нашем распоряжении масштаб времени.
Таким образом, необходимо, чтобы выполнялось условие
где λ — длина волны, с — скорость света в вакууме. Поскольку времена прохождения света от точек М и N до В равны, полученное условие можно переписать в виде
Из прямоугольных треугольников на рисунке 2 находим:
откуда, вычитая из первого равенства второе, получаем:
Приняв \(~l_1 + l_2 = 2l\) и \(~\frac{h}{l} = \sin \alpha\) , находим:
Тогда из условия (*) следует, что
— изображения двух точек окажутся различимыми, если расстояние между ними больше или хотя бы порядка длины световой волны. Для видимого света длина волны составляет примерно 0,5 мкм.
Чем меньше размеры предмета, еще различимого микроскопом, тем больше так называемая разрешающая способность микроскопа.
Примечание. Кроме обычных оптических микроскопов существуют электронные микроскопы, у которых разрешающая способность много больше. При их помощи можно даже рассмотреть отдельные молекулы.