Kvant. Молекулы, сосиски и алмазы

Стасенко А.Л. Молекулы, сосиски и алмазы //Квант. — 2003. — № 1. — С. 35-36.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Алмаз — чистый углерод, встречающийся в прозрачных кристаллах от мелких зерен,

видимых лишь в микроскоп, до кристаллов массой в 3000 карат (600 г).

…Согласно преданию, знаменитый «Коинур», или «Гора света», отнятый у короля Лахора английскими войсками,…

принадлежал королю Карна уже за 3 тыс. лет до н.э.

А.Ферсман. Рассказы о самоцветах

Как известно, потенциальная энергия взаимодействия двух точечных зарядов обратно пропорциональна расстоянию между ними (этот факт тесно связан с законом Кулона):

\(~W_p \sim \frac{q_1 q_2}{r}\) .

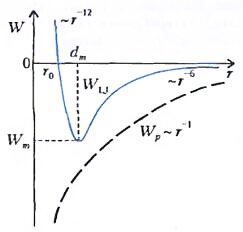
Если знаки зарядов противоположны, потенциальная энергия отрицательна - имеет место притяжение, а зависимость W_p(r) можно изобразить в виде бесконечно глубокой потенциальной «ямы» (рис.1; штриховая линия).

Рис. 1

Нейтральные молекулы тоже взаимодействуют друг с другом. На расстояниях r, значительно превосходящих их характерный размер d_m, они испытывают взаимное притяжение - поэтому газы и могут конденсироваться. При попытке же сблизить молекулы так, чтобы r стало меньше d_m, возникает сильное отталкивание - поэтому жидкости слабо сжимаемы. Значит, радиальная зависимость потенциальной энергии взаимодействия двух нейтральных молекул должна состоять из двух ветвей: резко падающей вблизи начала координат и затем плавно растущей и приближающейся к оси абсцисс (рис.1; сплошная кривая). Ясно, что в такой ситуации должно существовать значение межмолекулярного расстояния r = d_m, соответствующее минимуму потенциальной энергии W_m — дну той самой потенциальной ямы, куда стремятся «свалиться» молекулы, образуя конденсированное вещество.

Физики придумали много зависимостей потенциальной энергии взаимодействия молекул от расстояния между ними. Одна из них - потенциал Леннарда-Джонса - имеет вид

\(~W_{LJ} = 4W_m \left( \left( \frac{r_0}{r} \right)^{12} - \left( \frac{r_0}{r} \right)^6 \right)\) . (*)

В этом случае можно найти минимум функции и получить значение характерного размера молекул\[~d_m = r_0 \sqrt[6] 2\]. Поскольку в наших обозначениях r есть расстояние между центрами молекул, то d_m можно назвать диаметром молекул, а тогда их «собственный радиус» равен \(~\frac{d_m}{2}\).

Если молекула находится в глубине газа или конденсата, вдали от его границ, то она со всех сторон окружена другими молекулами. Однако если молекула расположена у поверхности конденсата, то у нее число соседей, а значит, и молекулярных связей, меньше, чем у молекул в глубине. Поэтому потенциальная энергия таких молекул будет другой.

Рис. 2

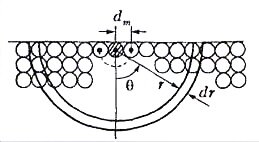
Рассмотрим одну из поверхностных молекул (заштрихована на рисунке 2) и найдем энергию ее взаимодействия со всеми остальными молекулами, заполняющими полупространство. Используя очевидную симметрию задачи, выделим шаровой слой, ограниченный полусферами с радиусами r и r + dr. Сколько молекул dN содержится в этом слое? Объем слоя равен 2πr²dr , концентрация молекул равна \(~n = \frac{\rho}{m}\) (ρ - плотность жидкости, m - масса одной молекулы), тогда

\(~dN = \frac{\rho}{m} \cdot 2 \pi r^2 dr\) .

Пусть потенциал парного взаимодействия описывается зависимостью (*). Тогда суммарная энергия взаимодействия выделенной нами молекулы со всем полупространством будет описываться легко вычисляемым интегралом:

\(~W_{\Sigma} = \frac{\rho}{m} \cdot 4W_m \int^{\infty}_{d_m} \left( \left( \frac{r_0}{r} \right)^{12} - \left( \frac{r_0}{r} \right)^6 \right) \cdot 2 \pi r^2 dr = 8 \pi \frac{\rho}{m} W_m \left( -\frac{r^{12}_0}{9r^2} + \frac{r^6_0}{3r^3} \right)^{\infty}_{r = d_m} = -\frac{10}{9} \pi \rho \frac{W_m}{m} d^3_m\) .

На каждую молекулу в поверхностном слое приходится площадь d²_m. Следовательно, поверхностная плотность энергии равна по величине

\(~w = \frac{10}{9} \pi \rho \frac{W_m}{m} d_m\) .

Подставим данные для воды: m = 18 · 1,67·10^-27 ≈ 3·10^-26 кг, ρ = 10³ кг/м³, d_m ≈ 3 А = 3·10^-10 м, W_m = 10^-20 Дж и получим w ≈ 0,35 Дж/м².

Но поверхностная плотность энергии есть величина порядка коэффициента поверхностного натяжения воды, который при комнатных условиях равен σ = 0,07 Дж/м². Как видим, наша оценка, хотя и завышена, весьма удовлетворительна, если учесть грубость сделанных предположений.

Но при чем тут сосиски и алмазы? Очень даже при чем, и не только они. Например, существование капель воды тоже обеспечивается поверхностным натяжением. Так, капли дождя радиусом a, падая в атмосфере, сплющиваются аэродинамической силой сопротивления, равной силе тяжести (в установившемся режиме). Приравнивая эту силу «восстанавливающей» силе поверхностного натяжения - порядка 2πaσ, - получим оценку предельного радиуса капли:

\(~m_kg \sim 2\pi a \sigma\), где \(~m_kg = \frac 43 \pi a^3 \rho\) ,

откуда

\(~a \sim \sqrt{\frac{\sigma}{\rho g}} = \sqrt{\frac{0,07}{10^3 \cdot 10}}\) = 2,6 мм,

что вполне реально (понаблюдайте за летним ливнем).

Рис. 3

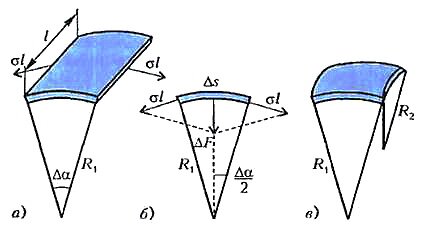
Это поверхностное натяжение в случае кривой поверхности вызывает дополнительное давление внутри объема жидкости. Рассмотрим небольшой участок цилиндрической поверхности с радиусом кривизны R₁ и центральным углом Δα (рис. 3,а). Если его длина l, то на каждую сторону действует сила, равная σl. Результирующая сила, как легко понять из рисунка 3,б, направлена к центру кривизны и равна

\(~\Delta F = 2 \sigma l \operatorname{tg} \frac{\Delta \alpha}{2} \approx \sigma l \Delta \alpha\) .

Учитывая, что длина дуги Δs связана с радиусом кривизны соотношением Δs = R₁Δα, получим

\(~\frac{\Delta F}{l \Delta S} = \frac{\sigma}{R_1}\) .

Но это ведь давление!

Понятно, что если участок поверхности не цилиндрический , а искривлен еще и в другой плоскости (радиус кривизны R₂; рис. 3,в), то получим большее давление:

\(~p_L = \sigma \left( \frac{1}{R_1} + \frac{1}{R_2} \right)\) .

(здесь индекс «L» подчеркивает наше уважение к Лапласу, чьим именем называют это избыточное давление под изогнутой поверхностью).

Из последней формулы ясно, например, почему сосиски при долгом кипении лопаются вдоль, а не поперек: натяжение их оболочки на цилиндрическом участке меньше, чем на сферических закруглениях, а давление содержимого можно считать постоянным во всех направлениях. Так же ведут себя и длинные газгольдеры - устройства для приема, хранения и выдачи газа.Конечно, в этих случаях поверхностное натяжение обеспечивается оболочкой сосиски или газгольдера.

А что же алмазы? Как известно, для их получения требуются высокие температуры и давления. Оказывается, и здесь на помощь приходит лапласовское давление. Оценим, какого размера алмаз можно получить из расплавленного углерода. Примем σ = 5 Дж/м², р = 60·10³ атм. Считая частицу сферической (R₁ = R₂ = a), из выражения для добавочного давления получим

\(~a = \frac{2 \sigma}{p}\) ≈ 15·10^-10 м = 15 А.

Конечно, мелковатые алмазы, но для многих технологий весьма полезные.

Итак, варя сосиски и думая об алмазах, не теряйте чувства меры, ибо не напрасно один литературный герой как-то сказал, что бриллиант в тысячу карат - это пошло.