Kvant. От пяди до Вселенной
Иншаков С. От пяди до Вселенной //Квант. — 2005. — № 5. — С. 29-31,34.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Человечество издавна пользовалось в своей практике измерениями. Вначале это были измерения, связанные с торгово-экономической деятельностью. Первое известное упоминание о точности и достоверности измерений встречается в Библии. Так, в одной из книг Пятикнижия сказано: «Не делайте неправды в суде, в мере, в весе и в измерении.... Да будут у вас весы верные, гири верные, ефа верная...» (Ефа — мера объема для сыпучих веществ, равная 52,48 литра.) А в другой книге устанавливается основная обязанность инспектора по обеспечению единства измерений: «В кисе твоей не должны быть двоякие гири, большие и меньшие... В доме твоем не должна быть двоякая ефа, большая и меньшая.. Гиря у тебя должна быть точная и правильная, и ефа у тебя должна быть точная и правильная, чтобы продлились дни твои на земле...» (Киса — это сумка. В современном русском языке сохранилось однокоренное слово кисет, обозначающее мешочек для махорки.)
В Древней Руси меры появились тоже очень давно, однако раздробленность княжеств приводила к тому, что меры длины, веса и объема по своему номинальному значению у разных князей различались в 1,5 - 2 раза. Единообразные меры возникли на Руси лишь с объединением княжеств в одно государство. Это — золотник (в последнем варианте 4,266 г), сажень (2,134 м), гривна (сначала денежная и весовая единица, затем счетно-денежная, равная 10 копейкам, отсюда — гривенник), пядь (расстояние между концами растянутых большого и указательного пальцев, равное 17,78 см) и др.
Тогда же был установлен и межповерочный интервал. Так, в грамоте князя Всеволода (XII в.) написано: «...торговая вся весы мерила и скалвы вощаные и пуд медовый и гривенка рублевка иже на торгу промеж людьми блюсти без пакости ни умалчивать ни умножати и на всякий год взвешивати...» (Надо полагать, скалвы — это единица меры воска, пуд — меда, а гривенка рублевка — денежная единица.) В той же грамоте указывались и санкции для нарушителей единства измерений: «...а скривится а кому приказано и того казнити близко смерти а живот его на трое...». В общем, плохо будет нарушителю.
Дальнейшее развитие законодательная метрология получила при Петре I. В одном из его указов написано: «По указу великого государя велено чтоб у торговых и мастеровых людей были весы и фунты у всех правдивые и заклеймены годовым клеймом...»
Однако в научных исследованиях роль единства измерений была осознана относительно поздно, лишь в XVIII веке, когда М.В.Ломоносов впервые ввел научные понятия меры и веса. Дальнейшее развитие метрологии как прикладной науки обеспечил во второй половине XIX века Д.И.Менделеев. Уместно привести высказывание знаменитого физика конца XIX века У.Томсона (лорда Кельвина): «Каждая величина известна лишь в той мере, в которой ее можно измерить».
Поговорим об измерениях в естественных науках на примере физики. Измерение — неотъемлемый атрибут физики. Как наука в нынешнем ее понимании, она стала оформляться в XVII веке (галилеево-ньютоновы времена). В то время она имела название «натуральная философия».
Чтобы начать изучать что-нибудь, необходимо это «что-нибудь» определить. Раз речь идет об окружающем мире, значит, это «что-нибудь» надо сначала увидеть, т.е. выделить из окружения (фона), установить различие между этим «что-нибудь» и фоном. Назовем это действие выявлением. Выявим сначала одно «что-нибудь», потом — другое «что-то». Теперь возникает проблема сравнения. Это сравнение можно проводить только по общему признаку. В самом деле, бесполезно, например, сравнивать звук, с которым первое «что-нибудь» падает на пол, и цвет поверхности второго «чего-то». (Для этого случая существует поговорка: «В огороде бузина, а в Киеве дядька».) Заметим при этом, что как общее (сравнение), так и различное (выявление) взаимосвязаны, они выступают в диалектическом единстве.
Пример 1
Рассмотрим арбуз и яблоко. Различить их можно по целому ряду признаков: цвету, запаху, вкусу, способности поглощать радиацию и т.д. Различили. Теперь будем сравнивать. Сравнивать надо по общему признаку. Возьмем в этом качестве объем. Его определим так: это воздух, который вытесняется тем или иным объектом из сосуда. Вот так от сравнения объемов разных тел перешли к сравнению одного и того же — воздуха. Введем теперь определение отношения «больше — меньше». Ясно, что из воздуха, вытесненного арбузом, можно сделать столько же воздуха, сколько вытеснило яблоко, а наоборот — нельзя. Это означает, что воздуха, вытесненного арбузом, больше, чем воздуха, вытесненного яблоком, т.е. объем арбуза больше объема яблока. Мы определили качественное отношение «больше — меньше».
Теперь определим количественное отношение, оно будет характеризоваться числом. Вот здесь и необходима процедура измерения. Сначала используем уже введенное качественное отношение. Рассмотрим такое общее свойство тел, как протяженность. Для простоты будем сравнивать протяженность в одном направлении и назовем тела, протяженности которых сравниваем, линейками. Методика сравнения такова: прикладываем линейки так, чтобы одни концы линеек находились напротив друг друга, и наблюдаем за оставшимися концами. Если они совпали, то линейки считаем равными. Если нет, то меньшей назовем ту, чей конец лежит напротив внутренней стороны другой линейки. Пока ничего нового — это качественное отношение, примененное не к объемам тел, как в примере 1, а к их протяженностям.
Сформулируем определение: измерением физических свойств называется процедура соотнесения этим свойствам некоторых чисел таким образом, чтобы сравнение свойств можно было теперь заменить сравнением этих чисел.
Другими словами, устанавливается взаимно однозначное соответствие между числами и свойствами. Математика здесь присутствует в механизме этого соотнесения. Итак, если исследуемое свойство характеризуется взаимно однозначным соответствием с числом, то оно называется физической величиной. Процедура нахождения этого числа и есть измерение.
Пример 2
Берем одну линейку и принимаем ее длину за единицу измерения. Длинам всех других линеек приписываем числа, равные количеству этих единичных линеек, укладывающихся на измеряемой протяженности. Выразим эту процедуру математически. Длина некоторой линейки выражается так: L = nL0, где n — безразмерное число, а L0 — единица измерения. Если теперь у нас две линейки, причем L1 = n1L0 и L2 = n2L0, и надо найти их суммарную длину (в безразмерных числах), то
Таким образом, при равномерном разбиении сумма длин линеек равна сумме безразмерных чисел, которые характеризуют длину каждой из них.
Пример 3
Выберем другой способ разбиения. Возьмем равномерно размеченную линейку и пронумеруем ее по следующему закону: начало — числом 1, первое деление — числом 2, второе — числом 4, ..., n-е деление — числом 2n. Это означает, что длина делений обозначена безразмерным числом по закону P = 2n. Пусть есть две линейки — длиной P1 и P2. Найдем длину линейки, которая получается при сложении этих двух (в безразмерных единицах Р). Теперь закон разбиения линеек неравномерный: 2N, где N — число делений. Но разметка делениями равномерная, поэтому N = n1 + n2. В единицах Р получаем
т.е.
Иными словами, в таких единицах и при таком законе нумерации делений длина суммы двух линеек равна произведению их длин. (Заметим, что именно так работала логарифмическая линейка — аналоговый калькулятор, широко использовавшийся вплоть до начала 80-х годов прошлого века. Единственное отличие в том, что для удобства пользования на шкале логарифмической линейки деления нумеровались с помощью натурального ряда чисел (1, 2, 3, ...), а длина делений была неравномерной.
Теперь поговорим более подробно об измерениях расстояний, а именно — больших расстояний: от одного метра до размера Вселенной.
Учитывая наши собственные размеры, измерять расстояния путем непосредственного прикладывания эталонных линеек реально лишь при длине этих эталонов порядка одного метра. На больших расстояниях используется геометрия. В 1821 - 1823 годах этим занимался К.Гаусс. Он измерил углы между вершинами гор Брокен, Хохехаген и Инзельберг (Германия), учел поправку на сферичность (наибольшее расстояние между вершинами было около 100 км, при этом на каждой из вершин угломерные геодезические приборы устанавливались по местной плоскости горизонта и эти плоскости не были параллельными). В результате он получил, что измеренная сумма внутренних углов треугольника отличается от 180° на 0,680 дуговой секунды. Гаусс считал, что эта величина находится в пределах ошибок измерений, поэтому пространство является евклидовым (в пределах точности этих измерений). Таким образом, мы можем пользоваться хорошо разработанным математическим аппаратом евклидовой геометрии.
На практике эта задача решается с помощью топографической съемки земной поверхности. На поверхности Земли строго определяется положение ряда пунктов — как в плане, так и по высоте. Положение нескольких пунктов (геодезической основы) определяется по астрономическим измерениям: широта находится по наблюдению небесных светил, а долгота — по сравнению местного времени в двух точках в один и тот же момент. Эти пункты считаются исходными, с ними геодезическими измерениями связаны все остальные. Так образуется геодезическая сеть, покрывающая поверхность Земли. Линии, соединяющие отдельные пункты, могут образовывать треугольники или многоугольники. Длина сторон этих геометрических фигур порядка 25 км. Поскольку такие расстояния трудно измерить непосредственно при обычной прозрачности атмосферы, берут базис длиной порядка 10 км, который служит основой для построения базисной сети. Она, в свою очередь, является основой для вычисления по тригонометрическим формулам длин сторон всех треугольников геодезической сети. Наиболее точные современные измерения базиса длиной 10 км производятся с ошибкой 2 мм. Именно таким образом определяются основные расстояния на суше.
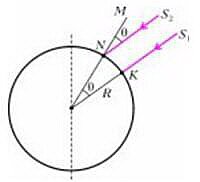
А вот для нахождения размера земного радиуса используются астрономические измерения. В один и тот же момент времени два наблюдателя смотрят прохождение одной и той же звезды через зенит. При этом наблюдатели должны располагаться на одном меридиане. Для более южного наблюдателя звезда в зените находится на луче KS1, для северного наблюдателя ее положение будет отличаться от местного зенита NM на угол θ (рис.1). Таким образом можно вычислить радиус земного шара R, зная расстояние между двумя точками N и K, находящимися на одном меридиане, и разность их географических широт.
Пример 4
Определим радиус земного шара по географической широте конкретных пунктов. Возьмем на карте Подмосковья на одном и том же меридиане два пункта — Большой Москворецкий мост, его широта 55°45’00’’, и мост через реку Упа в Туле, его широта 54°11’44’’. Расстояние между этими пунктами — 174 км вдоль меридиана. Используя связь между углом, образуемым радиусами окружности, и длиной дуги между ними, получаем \(~R = \frac{NK}{\theta}\) = 6391 км (естественно, угол надо брать в радианной мере). Реально радиус Земли равен 6378 км, отличие связано с тем, что Земля не совсем шар.
Расстояния в пределах Солнечной системы можно вычислять по известным периодам обращения планет и третьему закону Кеплера. Но так могут быть определены лишь относительные расстояния. Абсолютные же расстояния в пределах Солнечной системы находятся с помощью измерений горизонтальных параллаксов небесных светил. Параллакс — это угол, на который сместится объект наблюдения при перемещении наблюдателя на некоторое базовое расстояние. Для астрономических объектов базовое расстояние должно быть достаточно большим, в противном случае будет, как в стихотворении Пушкина, посвященном А.П. Керн:
«Я ехал к вам: живые сны
За мной вились толпой игривой
И месяц с правой стороны
Сопровождал мой бег ретивый...»
Другими словами, угловое смещение месяца при движении Александра Сергеевича в течение нескольких часов было совершенно незаметно, особенно по сравнению с громадным угловым смещением элементов пейзажа.
Оценим смещение Луны относительно звезд. Напомним, что суточное вращение Земли приводит к угловому перемещению небесной сферы со скоростью 15°/ч. Будем считать, что скорость повозки была около 15 км/ч, время поездки к Керн — не более 4 ч, тогда базовое расстояние получается порядка 60 км. Расстояние от Земли до Луны, как теперь известно, равно 384400 км, и угловое смещение Луны относительно звезд (без учета собственного движения Луны вокруг Земли) будет составлять 0,56’’ (или 78 микрорадиан), что на глаз абсолютно незаметно. Учтем собственное движение Луны вокруг Земли. Оно происходит с угловой скоростью 0,5°/ч, поэтому за 4 ч Луна сместится на 2° — на глаз тоже совсем незаметно. Поэтому для определения параллакса желательны одновременные измерения из двух мест с максимально возможной базовой. (Можно, конечно, проводить и не одновременные измерения, но тогда необходимо учитывать изменение положения светила за время между измерениями.)
На земле максимально возможная база — диаметр земного шара, вот почему традиционно за эталонную базу принимают земной радиус. Угол р между направлениями, по которым светило М было бы видно из центра Земли и из какой-нибудь точки на ее поверхности, называется суточным параллаксом светила. Иными словами, суточный параллакс есть угол, под которым со светила был бы виден радиус Земли, проведенный из центра Земли на ее поверхность (в исходную точку наблюдения). Если светило наблюдается на горизонте, то суточный параллакс максимален. В этом случае он называется горизонтальным параллаксом. Так как Земля имеет форму не сферы, а сфероида, то горизонтальные параллаксы вычисляются для одного конкретного радиуса. Это — экваториальный радиус Земли R0 = 6378 км , а горизонтальные параллаксы, вычисленные для него, называются горизонтальными экваториальными параллаксами p0. (Естественно, нет необходимости проводить астрономические наблюдения непосредственно на экваторе. Так как географические координаты обсерваторий известны, то результаты измерений, выполненных там, можно пересчитать на любую точку земной поверхности.) Именно эти параллаксы тел Солнечной системы и приводятся в справочниках. Горизонтальный параллакс у всех тел Солнечной системы весьма невелик — у Луны он равен 57’, у Солнца — 8,79’’, у большинства — планет меньше 1’.
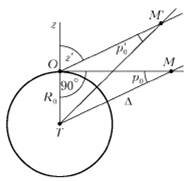
Зная горизонтальный экваториальный параллакс светила, легко определить его расстояние до центра Земли (рис.2). Из прямоугольного треугольника ТОМ имеем \(~\Delta = \frac{R_0}{\sin p_0}\). Для всех светил, кроме Луны, параллаксы очень малы, поэтому данную формулу можно написать иначе: положив \(~\sin p_0 = p_0'' \sin 1'' = \frac{p_0''}{206265}\), получим
Расстояние Δ получается в тех же единицах, что и радиус Земли R0, число 206265 является обратной величиной синуса одной дуговой секунды, а горизонтальный экваториальный параллакс берется в дуговых секундах. Наибольшее расстояние, которое наблюдается между Землей и самым дальним объектом Солнечной системы, равно 6055959000 км (p0 = 0,22’’). Это расстояние свет проходит за 5 часов 36 минут.
Появление и развитие радиолокации в середине XX века позволило непосредственно определить расстояния до ряда планет (вплоть до Юпитера). Они оказались именно теми, что были вычислены по горизонтальным экваториальным параллаксам.
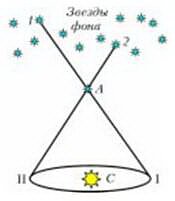
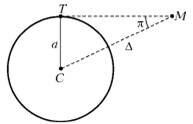
Расстояния от Солнца до ближайших звезд определяются с помощью годичных параллаксов. Принцип тот же, что и для суточных горизонтальных параллаксов, но база гораздо больше (рис.3). При этом рассматривается угловое смещение звезды относительно более удаленных звезд с полугодовым интервалом между измерениями, когда Земля переместится на расстояние диаметра своей орбиты. Угол, под которым был бы виден средний радиус земной орбиты при условии, что направление на звезду перпендикулярно радиусу, называется годичным параллаксом звезды и обозначается π (рис.4). Формула аналогична предыдущей, только в качестве базы теперь взят средний радиус земной орбиты а = 149600000 км:
Смещения эти совсем невелики. Так, ближайшая к нам звезда Проксима (в переводе с греческого — ближайшая) из созвездия Центавра имеет годичный параллакс π = 0,762’’. В результате наблюдений с Земли были измерены годичные параллаксы более 16000 звезд.
Наилучшие современные определения годичных параллаксов выполняются с космических аппаратов. Еще в 1966 году французский астроном П.Лакурт предложил использовать спутник для проведения массовых астрономических наблюдений. В 1975 году был создан и одобрен Европейским космическим агентством проект «Гиппаркос» — в переводе «спутник для сбора высокоточных параллаксов». Летом 1989 года космический аппарат был выведен на орбиту, и через несколько месяцев начались систематические наблюдения. В программу наблюдений было включено около 100 тысяч звезд, каждая из них наблюдалась 60 - 80 раз при точности единичного наблюдения 0,01’’, что в результате дало точность около 0,001 - 0,002’’.
В астрономии, помимо километров, приняты следующие единицы расстояний:
- астрономическая единица (а.е.) — среднее расстояние от Земли до Солнца (равное 149600000 км);
- парсек (пк), сокращенно от «параллакс» и «секунда» — расстояние, соответствующее годичному параллаксу в 1’’;
- световой год — расстояние, которое свет проходит за один год.
Соотношение между этими единицами таково:
- 1 пк = 30,86·1012 км = 206265 а.е. = 3,26 светового года;
- 1 световой год = 9,460·1012 км = 63240 а.е. = 0,3067 пк.
В астрономических единицах обычно выражают расстояния до тел Солнечной системы. Например, Меркурий находится от Солнца на расстоянии 0,387 а.е., а Плутон — на расстоянии 39,4 а.е. Расстояния до небесных тел за пределами Солнечной системы обычно выражаются в парсеках, килопарсеках (103 пк) и мегапарсеках (106 пк), а также в световых годах.
В настоящее время метод годичных параллаксов теоретически позволяет измерять расстояния до 1600 световых лет (Δ = 0,002’’). Но на таком большом расстоянии точность измерения уменьшается до 50%.
Еще большие расстояния удалось измерить другим методом, основанном на изучении закономерностей светимости переменных звезд. Во Вселенной встречаются переменные звезды двух типов — затменно-переменные, когда имеются две звезды, вращающиеся вокруг общего центра масс и при этом более яркая периодически затмевает менее яркую, и физически переменные, когда пульсирует одна звезда. Типичным представителем физически переменной звезды, регулярно меняющей свою яркость, является звезда δ созвездия Цефея. Все физически переменные звезды (а их достаточно много во Вселенной) принято называть цефеидами. В начале XX века в Гарвардской обсерватории (США) стали изучать цефеиды в соседней галактике, известной под названием Магелланового облака. Каждая цефеида имеет свой характерный период изменения яркости: от нескольких дней до сотен дней и более. Была найдена закономерность: чем длиннее оказывался период изменения яркости, тем ярче была сама звезда. А расстояние от Земли до Магелланового облака во много раз больше расстояния между самими звездами, т.е. с большой точностью их можно считать равноудаленными от Земли. Отсюда вывод: связь между периодом и яркостью носит абсолютный характер, цефеиды с одинаковым периодом обладают одинаковой яркостью. Поэтому, если на небе обнаруживались две цефеиды с одинаковыми периодами, но при этом яркость одной была в четыре раза меньше, то это означало, что она расположена вдвое дальше — яркость меняется обратно пропорционально квадрату расстояния.
Самое же большое из известных расстояний было измерено так. В оптике известен эффект Доплера — изменение частоты света, излучаемого объектом, при его приближении к наблюдателю или удалении от него. В акустике этот эффект тоже существует — каждый, кто находился на железнодорожной платформе при прохождении сигналящей электрички, мог убедиться, что при приближении тон сигнала высокий, а при удалении низкий. По изменению частоты можно вычислить относительную скорость. В двадцатые годы прошлого века астрономы в результате измерений доплеровского смещения спектральных линий света от галактик обнаружили, что почти все они разлетаются, и в ряде случаев с очень большой скоростью. Так, скорость удаления от нас галактик в созвездии Девы составляет около 1000 км/с. А сейчас найдены объекты, удаляющиеся со скоростями порядка 0,8 скорости света (240000 км/с). В конце 20-х годов прошлого века американский астроном Э.Хаббл показал, что скорость относительного движения галактик пропорциональна расстоянию между ними — более далекие от нас галактики имеют большую скорость, чем близкие. Связь между скоростями галактик и расстоянием до них устанавливается законом Хаббла: υ = HL, где коэффициент пропорциональности Н называют постоянной Хаббла. В настоящее время значения постоянной Хаббла, оцениваемые различными авторами, лежат в пределах от 60 до 80 км/(с·Мпк). Обычно используется значение постоянной Хаббла 75 км/(с·Мпк). При этом расстояние до объекта, имеющего скорость 240000 км/с, оказывается равным
Таково наибольшее измеренное к настоящему времени расстояние — самый «край» Вселенной.