Kvant. Полеты в струе
Митрофанов А. Полеты в струе и наяву //Квант. — 1991. — № 9. — С. 2-10.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Какое действие оказывает среда на двигающееся в ней тело? Скажем, если вы играете во дворе или идете по улице, вы почти не замечаете, что среда (воздух) оказывает вам какое-либо сопротивление. И опоздавший на урок ученик вряд ли станет утверждать, что основной причиной опоздания является сила сопротивления среды. Но стоит только чуть высунуть руку в открытое окно мчащегося поезда или попасть в поток сильного ветра, как вопрос о сопротивлении среды перестанет казаться бессмысленным. Воздух, обычно такой невесомый, неосязаемый, при больших скоростях начинает вдруг напоминать упругую стенку или непреодолимую преграду. Именно такие ощущения ждут пилота скоростного самолета, если ему придется катапультироваться в полете. Со свойством среды оказывать сопротивление движущемуся в ней телу хорошо знакомы не только авиаторы или космонавты, но и люди многих других, в том числе самых «земных» профессий.
Одно из первых научных исследований сопротивления среды принадлежит Ньютону[1]. Так как в то время было накоплено слишком мало данных о взаимодействии движущихся тел со средой, Ньютон вынужден был сам экспериментировать с бросанием тел. В 1710 и 1719 годах в соборе св. Павла в Лондоне он ставил опыты с движущимися в воде шарами. Из экспериментов ученый определил коэффициент в выведенной им же формуле для силы сопротивления, действующей на двигающееся в среде тело.
В наш век скоростного транспорта, сверхзвуковой авиации и спускаемых космических аппаратов многие старые задачи и экспериментальные методики аэро- и гидродинамики не утратили своего значения.
Поэтому интересно вспомнить кое-что из идей ученых прошлого и проделать опыты, которые познакомят вас с некоторыми физическими явлениями, возникающими при движении тел в среде.
Что же такое сопротивление среды? Двигающееся в жидкости или
газе тело оказывает воздействие на частицы среды, изменяя их скорость. По третьему закону Ньютона, на тело со стороны среды действует противоположно направленная сила, которую называют силой сопротивления. Рассмотрим составляющую силы сопротивления, которая направлена вдоль линии движения (скажем, оси X) и которую авиаторы называют лобовым сопротивлением. Из принципа относительности Галилея следует, что для определения этой силы при равномерном движении безразлично, двигается ли тело в неподвижной среде, или с такой же скоростью двигается ему навстречу среда, а тело неподвижно. Начнем с простого примера.
Пример 1
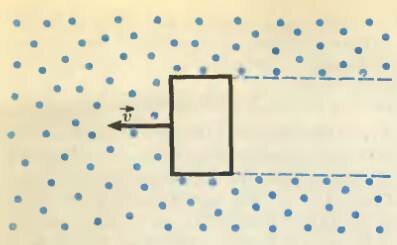
Пусть диск, шар или цилиндр радиусом R двигается со скоростью υ вдоль своей оси в пространстве, заполненном множеством не взаимодействующих друг с другом неподвижных частиц (рис. 1; масса каждой частицы m, их концентрация n). Что это за частицы? Можно представить себе, например, разреженный холодный газ, в котором не учитывается движение молекул. Прав будет также и тот, кто представит себе, что частицы — это снежинки, а задача описывает движение снежного кома (попросту снежка), летящего в воздухе и сталкивающегося со снежинками, которые прилипают к нему при столкновениях, и т. д.
В единицу времени тело встречает на своем пути \(~N = n \upsilon S\) частиц, где \(~S = \pi R^2\) — площадь поперечного сечения тела. Если столкновения частиц с телом неупругие, то сила сопротивления равна
где \(~\rho = mn\) — плотность среды.
Подобным образом можно рассчитать силу сопротивления Fx, действующую на тело с произвольным профилем. Надо только знать скорость, плотность и площадь столба частиц, с которыми сталкивается тело при движении в разреженной среде.
Несколько сложнее обстоит дело, когда удар упругий, т. е. когца частицы при ударе о произвольную поверхность отскакивают от нее. Но и в этом случае \(~F_x \sim \upsilon^2\), только коэффициент пропорциональности в формуле (1), вообще говоря, зависит от формы тела.
Пример 2
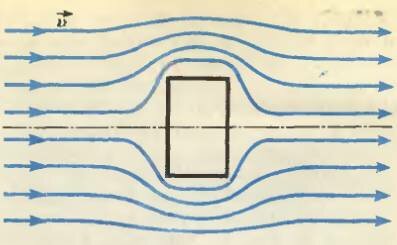
До сих пор мы рассматривали движение в разреженной среде. А как быть, если тело двигается с постоянной скоростью в жидкости, например в воде или в плотном газе (воздухе), т. е. в сплошной среде? Чем сплошная среда отличается от системы невзаимодействующих частиц? Ведь сплошная среда, будь то жидкость или плотный газ, тоже состоит из молекул или атомов. Но если в разреженной среде частицы двигаются независимо друг от друга, испытывая лишь редкие столкновения, то в сплошной среде частицы выступают уже как «коллектив». Действительно, расстояние между частицами (точнее, средняя длина свободного пробега молекул) во много раз меньше, чем характерный размер тела. Из-за взаимных столкновений частиц и влияния их друг на друга возмущения среды вблизи границы тела, возникающие при его движении, передаются соседним элементам среды. Следовательно, с движущимся телом взаимодействуют не только те объемы жидкости или газа, которые находятся точно на пути тела, но и соседние с его траекторией объемы среды, которые тело расталкивает или увлекает за собой (рис. 2).
Как зависит Fx от υ и от параметров среды? Ясно, что если скорость изменится, то при установившемся движении приблизительно пропорционально υ изменится масса жидкости М, с которой в единицу времени встретится и провзаимодействует тело, т. е. \(~M \sim \rho \upsilon S\), где S — площадь поперечного сечения тела, ρ — плотность среды. А каждый элемент этой массы передаст телу импульс, также примерно пропорциональный и. Поэтому зависимость силы сопротивления от скорости тела, рассмотренная впервые Ньютоном, имеет вид (сравните с формулой (1))
или в другой записи
где величина \(~\frac{\rho \upsilon^2}{2}\) называется динамическим давлением. (Она имеет размерность давления и есть ни что иное, как кинетическая энергия единицы объема движущейся среды, в которой находится неподвижное тело.) Коэффициент пропорциональности Cx в формуле (2) зависит в первую очередь от формы тела и, вообще говоря, от режима течения и скорости, если та изменяется в достаточно широких пределах. В аэродинамике эта величина называется коэффициентом лобового сопротивления, в гидродинамике — коэффициентом увлечения или коэффициентом гидродинамического сопротивления.
Сравнивая рисунки 1 и 2, отметим существенную разницу этих двух примеров. Жидкость обтекает тело, а не оставляет за ним «тень» пустого пространства, как при движении в разреженной холодной среде. Следовательно, сплошная среда оказывает давление на тело не только спереди (т. е. на носовую часть, если речь идет о корабле), но и с других сторон. С тыльной стороны тела (т. е. с кормы) направление действующей на тело силы совпадает с направлением движения. Таким образом, обтекание тела жидкостью или плотным газом приводит к уменьшению результирующей силы сопротивления Fx. Обтекая тело, жидкость сохраняет часть своего импульса, не передавая его телу. Это очень важное обстоятельство. С уменьшением коэффициента гидродинамического сопротивления вследствие обтекания тела потоком мы познакомимся, проведя следующий эксперимент.
Пример 3
Определим гидродинамическое сопротивление, которое испытывает шарик, плавающий под струей жидкости, и найдем коэффициент Cx для шарика в потоке. Этот простой эксперимент не потребует сложного оборудования. Нам нужны будут только ведро или ванна, мерный стакан или банка известного объема, линейка, часы с секундной стрелкой и легкий шарик, например пластмассовый шарик для настольного тенниса или небольшой резиновый мячик.
Откроем водопроводный кран. И вот в емкости уже достаточно много воды. Если положить шарик на воду, то он, как и следовало ожидать, поплывет прочь от струи. Но стоит только поместить шарик в струю или же подтолкнуть его к ней вплотную, как шарик сразу же захватится струей и... останется в ней на том месте, где струя встречается с поверхностью воды.
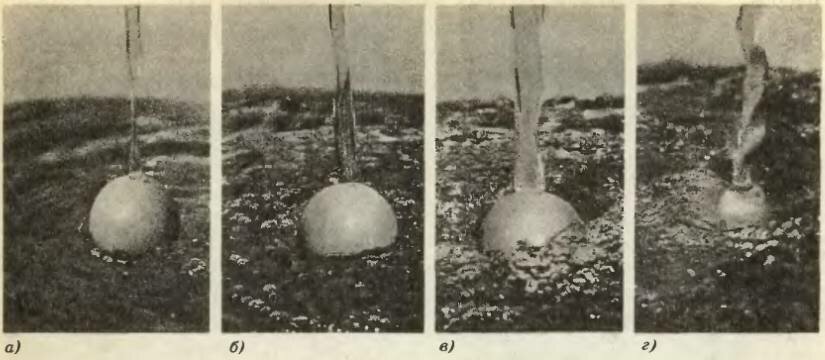
Посмотрим, что будет с шариком, если изменить напор воды в струе. Когда скорость струи небольшая, шарик плавает на поверхности (рис. 3, а) и может оставаться около струи сколь угодно долго. Иногда центр шарика смещается в строну от осевой линии струи, а шарик при этом вращается вокруг некоторой горизонтальной оси, как маленькая турбинка.
С увеличением напора воды шарик глубже погружается в воду, перестает вращаться и его центр устанавливается на осевой линии струи, совершая еле заметные колебания (рис. 3, б, в). И наконец, если открыть кран еще больше, шарик совсем скроется под водой (рис. 3, г).
Погружение легкого пустотелого шарика происходит главным образом благодаря гидродинамическому сопротивлению — силе, действующей на него со стороны потока. Эту силу легко измерить, если контролировать глубину погружения шарика.
Подберем напор воды таким, чтобы шарик погрузился в воду на определенную глубину, скажем на величину радиуса шарика, и находился в равновесии. Такое погружение удобно фиксировать на глаз. В равновесном положении сила Архимеда FA уравновешивает силу тяжести шарика mg и силу сопротивления Fc:
В этом уравнении \(~m = \frac 43 \rho_{sh} \pi R^3\), где R — радиус шарика, а ρsh — его средняя плотность. Радиус шарика для пинг-понга равен R ≈ 1,9 см, его масса m ≈ 2,5 г, т. е. ρsh ≈ 0,09 г/см3, что примерно в 11 раз меньше плотности воды ρv = 1 г/см3 (поэтому шарик плавает, почти не погружаясь). Сила Архимеда, действующая на шарик, погруженный наполовину, равна \(~F_A = \frac 43 \pi R^3 \frac{\rho_v}{2}\). Для Fc используем формулу Ньютона (2), подставив туда \(~S = \pi r^2\), где r — радиус струи. Получим
откуда выразим коэффициент гидродинамического давления Cx:
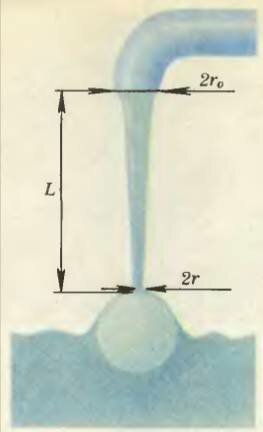
Чтобы найти отсюда значение Cx, надо знать еще величины r и υ, которые измерить непосредственно не так-то просто. Но их можно определить косвенно (рис. 4), если измерить объемный расход воды в струе Q (\(~Q = \pi r^2 \upsilon\) — объем воды, проходящий через сечение в единицу времени), ее длину L, начальный радиус r0 (у горловины крана) и воспользоваться тем, что расход воды в любом сечении струи — один и тот же (так называемое уравнение непрерывности струи):
где υ0 — скорость потока у горловины крана. (Расход воды можно измерить, наливая ее в мерный сосуд и засекая время. Зная Q и r0, найдем \(~\upsilon_0 = \frac{Q}{\pi r^2_0}\). Зная υ0 и L, вычислим \(~\upsilon = \sqrt{\upsilon^2_0 + 2gL}\), а потом и r из уравнения (4)). Прежде чем проводить измерения, подумайте, каков смысл уравнения (4), почему струя утончается книзу и по какому закону уменьшается ее радиус (см. пример. 4).
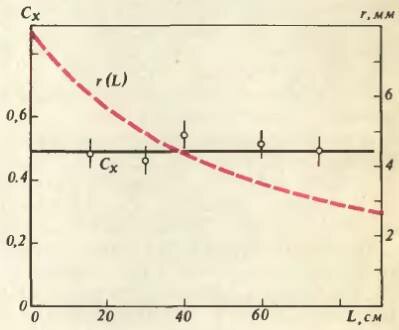
Проведем измерения. И вот результат. Для того чтобы шарик от пинг-понга затонул под струей наполовину, для струи длиной L = 60 см с начальным радиусом r0 = 0,8 см расход воды Q должен быть примерно равен 130 см3/с. Отсюда для Cx получается значение, близкое к 0,5. Если в опыте изменить длину струи L, то надо будет изменить и расход воды в струе, чтобы шарик оставался затопленным на ту же глубину. Однако, независимо от того, каков расход воды, величина Cx остается практически той же самой. Результаты наших измерений Cx при разных расходах воды в струе показаны на рисунке 5; пунктирная кривая — расчетные значения диаметра струи D = 2r, который она имеет вблизи точки ее контакта с шариком. Проверьте самостоятельно, что для струй разной длины, независимо от величин r и υ, получается приблизительно одно и то же значение коэффициента гидродинамического сопротивления, а именно Cx = 0,5 ± 0,1.
Попробуем теперь осмыслить полученный результат. При расчете силы сопротивления Fx мы использовали формулу Ньютона (2). Во-первых, так как эта формула хорошо описывает эксперимент (Cx почти не меняется), то можно сказать, что мы проверили ее справедливость (в диапазоне скоростей υ ≈ 1 - 10 м/с). Во-вторых, измеряя значение Cx, мы получили, что, как ни странно, шарик «отбирает» только около 1/4 импульса струи, остальное «уходит» в воду, в которой плавает шарик: коэффициент гидродинамического сопротивления оказался равным около 1/2, а не 2, как это было бы в случае абсолютно неупругого «удара» струи о шарик! (см. формулу (1)).
Последний экспериментальный факт не является таким очевидным. На первый взгляд кажется, что узкая струя, падая на почти плоскую вершину шарика (\(~r \ll R\)), должна передавать ему большую часть своего импульса. В действительности, как мы видим, струя огибает шарик почти без потери скорости и уходит под ним в воду, сохранив значительную часть (три четверти!) своего импульса. Обтекание тела потоком уменьшает гидродинамическое сопротивление!
Кое-кто из любителей физики скажет, что числа 1/4 или 1 — это по порядку величины один и тот же множитель. Верно. Но не все задачи можно решать с точностью до порядка. Ведь никто не станет отрицать, что есть ощутимая разница в том, наливать ли в топливные баки, скажем, 400 т горючего или же загружать их только на 100 т. Как раз на преодоление сопротивления среды расходуется львиная доля энергии двигателей подводной лодки, скоростного автомобиля или электровоза. Поэтому уменьшение величины Cx даже на несколько процентов надо расценивать как достижение.
Пример 4
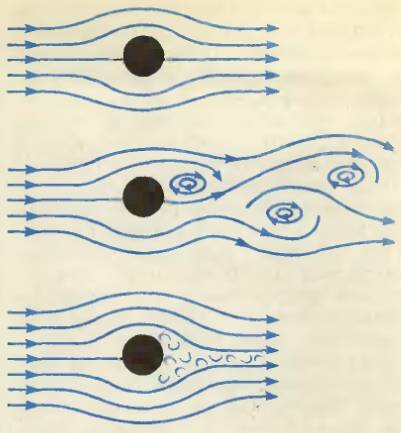
Формулой (2) с упехом пользуются на практике, скажем, когда оценивают силу давления ветра на парус или здание, силу сопротивления, действующую на двигающийся объект, будь то самолет, птица, автомобиль или подводная лодка. В аэродинамике формула (2) — одна из основных. Однако надо иметь в виду следующее. Поскольку давление в потоке зависит от скорости течения, то результирующая сила гидро- или аэродинамического сопротивления зависит от того, как жидкость или газ обтекает тело: какова скорость среды вблизи поверхности, плавное ли течение или оно с завихрениями, где на границе тела происходит так называемый срыв потока при обтекании и т. д. Именно многообразие видов течений сплошной среды вблизи тела (см., например, рис 6) часто приводит к трудностям при определении величин Fx и Cx. Для таких тел, как шар, диск (поперек потока), не очень длинный цилиндр и т. д., величина Cx в широком диапазоне скоростей обычно порядка 0,1 - 1. Для хорошо обтекаемого удлиненного каплеобразного тела с закругленной головной частью коэффициент сопротивления может достигать значений 0,04 - 0,06.
Еще в несколько раз меньшее значение коэффициента гидродинамического сопротивления, вплоть до величин около 0,01, может быть у рыб и некоторых водных животных при плавании их в воде. Классический пример тому — дельфины. Правда, такие животные и рыбы не только имеют обтекаемую форму, но «применяют» еще и целый комплекс хитростей: специальные кожные покрытия, жировую смазку или слизь на чешуе, уменьшающие сопротивление при движении, и, кроме того, с помощью движений мышц активно управляют потоком, предотвращая возникновение завихрений, в которые могла бы «перекачиваться» энергия дельфина или рыбы. В этом направлении животные «обогнали» инженеров и ученых-гидромехаников — не все еще «технические решения» живой природы реализованы в конструкциях, созданных человеком. Здесь есть над чем поработать инженерам...
Пример 5
Еще на заре развития поршневой авиации в опытах по измерению лобового сопротивления в аэродинамических трубах было обнаружено неожиданное явление. При сравнительно больших скоростях воздушного потока с увеличением его скорости лобовое сопротивление шара (и некоторых других тел) в какой-то момент времени резко уменьшалось в несколько раз. Исследователям удалось определить условия, при которых наблюдается такой скачок, измерить его и объяснить эффект. Он оказался связан с перемещением точки срыва потока при увеличении его скорости и уменьшением ширины вихревой зоны позади тела. Улучшение условия обтекания тыльной части тела приводило как раз к уменьшению коэффициента Cx. Хотите познакомиться с одним интересным следствием этого явления?
Оказывается, что если бы на Земле шел очень крупный град и диаметр градин при их падении возрос до Dкр = 13 см, то скорость града увеличилась бы скачком в 2,5 раза от 160 до 400 км/ч! (По другим оценкам получается, что Dкр чуть меньше 10 см.) Есть сведения, что в наши дни выпадает град величиной с куриное яйцо или даже с апельсин. Но кто знает, быть может, когда-то падал и более крупный град (вплоть до размеров Dкр)? Ведь раньше атмосферная «машина» на планете работала активнее, грозы, дожди и град были более сильными! Возможно, здесь кроется объяснение загадочного исчезновения динозавров. Их просто побил крупный, быстрый град! Мелким животным по понятным причинам удалось избежать столь печальной участи...
Пример 6
Формула Ньютона для расчета силы сопротивления справедлива далеко не всегда. Эта формула не позволяет, например, правильно вычислить силу, действующую на ложку, которая погружается в банке с медом. Она не описывает, как тонет маленький стальной шарик в высоком сосуде с растительным маслом, и уж совсем не может объяснить, почему так долго опускается молочный туман, который любят грибники и который доставляет столько неприятностей водителям, речникам и авиаторам.
Во всех перечисленных случаях для определения силы сопротивления надо знать не только форму и размеры тела, скорость относительного движения в среде и ее плотность, но и еще одну характеристику среды, которая называется коэффициентом вязкости и обычно обозначается буквой η). Этот коэффициент показывает, сколь велико или мало в жидкости или газе внутреннее, или, как говорят, вязкое трение.
Если силы вязкости являются при движении шарика в среде определяющими, то шарик испытывает тормозящее сопротивление, которое можно вычислить по формуле Стокса
а не по формуле Ньютона (2).
Но как узнать, является ли среда вязкой и какую формулу надо использовать при определении силы сопротивления в каждом конкретном случае?
Рассмотрим сферическую капельку воды, свободно падающую в воздухе (или шарик-градину, пренебрегая разницей в плотностях воды и льда). Будем интересоваться установившейся скоростью падения капли, которую можно измерить и из условия динамического равновесия найти, как зависит лобовое сопротивление от скорости, размера капли и параметров среды (ее плотности и коэффициента вязкости). Массу капли будем считать постоянной, т. е. пренебрежем конденсацией паров и испарением влаги с капли.
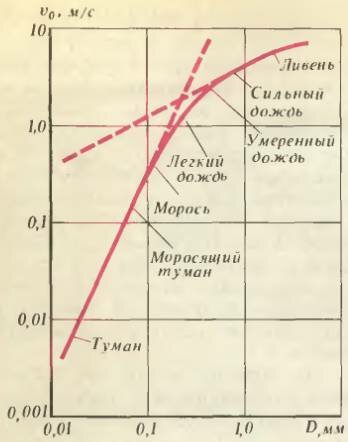
На рисунке 7 показан график зависимости скорости падения дождевых капель от их диаметра. Данные взяты из пособия по метеорологии. Рядом с кривой указано, при каких атмосферных осадках, как правило, наблюдаются капли данного диаметра.
Из рисунка видно, что самые мелкие капельки (диаметром 0,01 - 0,1 мм) падают со скоростью \(~\upsilon_0 \sim D^2\). Это возможно, только если сила сопротивления описывается формулой Стокса, из которой следует выражение для скорости осаждения частиц тумана:
где η ≈ l,8·105 кг/м·с при T = 300 К. Для воздуха и других газов величина \(~\eta \sim \sqrt T\) и почти не меняется с изменением плотности газа.
С увеличением размеров капли и скорости движения относительный вклад сил вязкого трения, пропорциональный \(~\eta \upsilon R\), уменьшается по сравнению с силами, пропорциональными величине \(~R^2 \frac{\rho \upsilon^2}{2}\), для которых записана формула Ньютона (их иногда называют инерциальным откликом среды, чтобы не путать с силами вязкого трения).
Крупные капли дождя (диаметром D ≥ 1 мм) почти «не чувствуют» вязкое трение воздуха. Для них скорость установившегося падения в атмосферном воздухе пропорциональна \(~\sqrt D\) и равна
где Cx ≈ 0,5. Это выражение получается из формулы (2).
Надо иметь в виду, что формула (5) носит приближенный характер, так как, в отличие от капелек тумана и града, крупные капли дождя имеют форму, заметно отличную от сферической. Силы поверхностного натяжения воды не в состоянии «справиться» с динамическим давлением набегающего потока воздуха, деформирующего каплю. Самые крупные капли (D ≥ 5 мм), достигая скорости около 8 м/с, сплющиваются столь сильно, что разбрызгиваются на более мелкие.
Для капелек диаметром 0,1 мм ≤ D ≤ 1 мм не работает ни формула Стокса, ни формула Ньютона. Для таких капелек силы вязкого трения и инерциальный отклик среды соизмеримы.
Пример 7
Есть еще один — третий — механизм торможения тел, который тоже часто встречается на практике и который при некоторых условиях может стать определяющим.
Налейте в ведро или ванну воды и погрузите в нее карандаш вертикально на некоторую глубину. Начните перемещать карандаш параллельно поверхности воды. Если скорость карандаша небольшая, то ничего интересного вы не заметите. Но если карандаш перемещать быстро, то за ним образуется расходящаяся группа волн, которая будет нести определенную энергию. На образование волн расходуется мощность двигателя (в данном случае руки), преодолевающего сопротивление среды.
По нашему опыту мы знаем, что за движущимся телом часто возникают волны, и они могут быть весьма разнообразными. Картина волн от корабля или моторки в глубокой воде отличается от мелких капиллярных волн, которые можно наблюдать в ведре, стакане или блюдце. Волны от моторной лодки на мелководье имеют иной вид, чем в глубокой воде. Сверхзвуковой самолет создает ударную волну в трехмерной среде (воздухе), а не на поверхности раздела (воды и воздуха), как корабль. К тому же, в отличие от обычных волн на воде, ударная волна в газе сопровождается сильным сжатием среды и ее разогревом.
Волновое сопротивление зависит от того, как возбуждаются волны, т. е. от свойств среды, в которой происходит движение, от скорости и характера движения, формы, прежде всего носовой части, и размеров тела. Обычно волновое сопротивление резко растет с ростом υ, если, конечно, тело с увеличением υ не выскакивает из воды, как скуттер или судно на подводных крыльях.
В каждом конкретном случае расчет величины волнового сопротивления, представляет сложную задачу, которую обычно удается решить, только прибегая к услугам эксперимента, используя эмпирические данные. Но сравнительно просто оценить, сколь велико может быть волновое сопротивление.
Рассмотрим, например, прямолинейное и равномерное движение моторной лодки по глубокому озеру. От корпуса моторки расходятся симметрично по курсу две косые волны — носовая и кормовая, которые, складываясь, дают характерную картину волн, хорошо знакомую всем рыбакам и любителям плавания. Угол α, который образуют гребни волн с направлением движения лодки, не зависит от ее скорости и равен около 20°. С каждой стороны от линии курса лодки выделяются 2 - 3 небольших гребня. Амплитуды остальных волн значительно меньше, так что при оценках можно совсем не обращать на них внимания — они вносят малый вклад в общий результат. Волны от лодки распространяются на сотни метров, слабо затухая со временем.
Гребень волны будем приближенно считать треугольником высотой Н, отмеряя эту величину от равновесного уровня озера. Длина основания треугольника равна \(~\frac{\lambda}{2}\), где λ — длина распространяющейся от лодки волны. Протяженность фронта волн, которые рождаются в единицу времени, численно равна υ cos α. Работа, затрачиваемая на создание гребня, переходит в потенциальную энергию волны. Поэтому с учетом кинетической энергии волн, которая в периодических процессах равна потенциальной, для мощности, необходимой для создания группы волн за лодкой, получим оценку
где 2n — полное число гребней волн за лодкой. Множитель \(~\frac H3\) — это средняя (с учетом распределения массы в гребне) высота подъема воды.
Вот типичный пример. При скорости моторки 18 км/ч за ней бегут волны высотой 0,3 м и длиной около 0,6 м, n = 3. По формуле (6) получаем, что W ≈ 3·103 Вт ≈ 4 л. с. С точностью до множителя 2 этому же равна минимальная мощность мотора, с помощью которого на небольшой лодке удается достигнуть указанной скорости.
Таким образом видно, что существенная доля мощности двигателя моторной лодки расходуется на создание волн.
Задачи и вопросы
- Изучая падение тел, Галилей бросал с башни одновременно пушечное ядро массой 80 кг и мушкетную пулю массой около 200 г. Существенным ли было в этом опыте влияние воздуха на время падения тел? Высота башни равнялась около 60 м.
- Новая модель локомотива отличается от старой только двигателем, мощность которого в 1,5 раза больше прежней. Во сколько раз максимальная скорость нового локомотива больше, чем старого?
- Чем вызван разброс экспериментальных точек на графике на рисунке 4? Определите значение коэффициента Cx, в опыте при полном погружении шарика под струей воды, аналогично примеру 3, рассмотренному в статье. Какие выводы можно сделать на основании вашего результата? Что можно сказать о точности эксперимента?
- Покажите, что в точке, находящейся на расстоянии L от горловины крана, радиус струи r определяется выражением \(~r(L) = r_0 \left( 1 + \frac{2gL}{\upsilon^2_0} \right)^{-\frac 14}\) где υ0 — скорость воды, вытекающей из крана, g — ускорение свободного падения, r0 — начальный радиус струи. Струя не разбрызгивается на капли, эффектами трения и поверхностного натяжения можно пренебречь.
- Каким образом можно сделать видимым течение жидкости в воде под шариком? Проведите соответствующий опыт с водопроводной струей. Каков характер течения жидкости под шариком?
- Если взять за ручку столовую ложку и подставить ее под струю воды, то реакция струи на ложку будет заметно разная, в зависимости от того, выпуклой или вогнутой поверхностью повернута ложка к струе. Почему?
- Чему равняется равновесная скорость υ0, с которой падает в воздухе шарик от настольного тенниса?
Ответы
- 1. В опыте Галилея мушкетная пуля и ядро достигали земли практически одновременно. Скорость тел вблизи земли около 30 м/с, время падения около 3,5 с. Однако, если бы Галилей фиксировал интервалы времени более короткие, скажем порядка 10-2 с, он заметил бы, что мушкетная пуля чуть-чуть отстает от ядра: относительный вклад сопротивления воздуха для падающей пули больше, чем для ядра.
- 2. В \(~\sqrt[3] {1,5} \approx 1,15\) раза.
- 5. Если, не изменяя течение струи, добавить в нее небольшое количество красителя, например чернила или марганцовку, то видно, что под шариком течение носит хаотический, турбулентный характер.
- 6. Коэффициент Cx сильно зависит от ориентации ложки относительно направления струи.
- 7. Если в воздухе с большой высоты уронить шарик для настольного тенниса, то за время τ ≈ 2 - 3 с устанавливается равновесное падение со скоростью около 8 м/с.
Примечания
- ↑ Кроме Ньютона, этими вопросами занимались Леонард Эйлер, Жан Лерон, д'Аламбер, Даниил Бернулли, Шарль Кулон и многие другие ученые. Читателям, интересующимся историей гидро- и аэродинамики, можно рекомендовать книгу из серии «Жизнь замечательных идей»: Г. Смирнов «Рожденные вихрем» (М.: Знание, 1982).