Kvant. Поливка
Стасенко А.Л. Как студент огород поливал //Квант. — 2000. — № 1. — С. 31,34.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
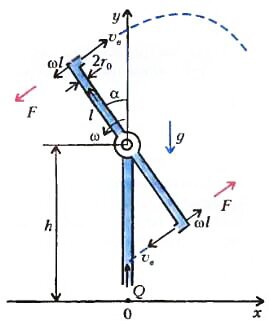
Как-то раз давным-давно, попросила бабушка внука-студента огород полить. И шланги были, и воду компрессором подали - да вот в чем закавыка: Студент был умный да еще вычитал, что «уже в 450 году до нашей эры «Кратет высказал мнение о необходимости сначала постепенной, а потом и полной замены ручного труда... автоматами». Опустил он буйну голову на широку грудь, а в груди была дума крепкая. Вспомнил он сегнерово колесо и представил себе трубку с концами, отогнутыми в противные стороны, да насаженную на другую трубу, подающую воду, причем та, что первая, могла свободно вращаться за счет реакции вытекающей струи. Ввел Студент обозначения (рис.1) и снова задумался.
Если υv — скорость движения воды внутри трубки с площадью сечения S, то секундный расход воды через одно отверстие равен Q = ρvυvS. А так как жидкость несжимаема и, значит, ее плотность ρv постоянна, при постоянной величине S скорость воды одинакова в любом сечении трубки. (Тут Студент почувствовал, что он применил закон сохранения массы.) Если в результате выброса воды трубка длиной 2l приобрела угловую скорость ω, то линейная (окружная) скорость ее концов будет равна ωl и направлена противоположно скорости υv движения воды, так что в системе координат, связанной с огородом, скорость истечения воды будет равна по величине υ0 = υv - ωl. Следовательно, поток импульса через одно отверстие равен Q(υv - ωl), а его размерность есть кг/с · м/с =Н. Но ведь это же размерность силы F!
Таким образом, имеется пара сил - две равные по величине силы, параллельные и противоположно направленные, причем l - плечо каждой силы относительно оси вращения. В результате на трубку действует момент сил
Но до какой угловой скорости может раскрутиться трубка? И вообще, мешает ли ей что-то неограниченно ускоряться во вращательном движении? Конечно. Ну например, момент сил трения во втулке (куда же деться от трения!), сопротивление воздуха... Уж очень хотелось Студенту сказать привычные слова «сопротивлением воздуха пренебречь», но как честный человек он решил прежде всего сделать численную оценку.
Ему давно было известно, что сила сопротивления воздуха движущемуся телу пропорциональна квадрату скорости υ тела относительно воздуха, площади поперечного сечения S⊥ тела и плотности воздуха ρ. Но чтобы ею пренебречь, нужно эту силу сравнить с какой-нибудь другой, которая предполагается существенно важной. Скажем, с потоком импульса массы воды, истекающей из трубки (в системе координат, связанной с самой трубкой), равным Qυv:
Здесь для усиления неравенства взято наибольшее изменение скорости: υ = ωl, достигаемое на конце трубки, и, конечно, пренебрежено тем, что трубка при своем вращении увлекает в движение воздух. Итак, завершим оценку. Ясно, что ωl не может превосходить υv — иначе трубка не будет раскручиваться, отношение плотностей воздуха и воды \(~\frac{\rho}{\rho_v}\) составляет приблизительно 10-3, и если взять трубку «разумных размеров» - например, l ~ 10 см и 2r0 ~ 1 см, то для искомого отношения двух сил получим величину порядка и менее 10-2. Значит, с точностью до процентов можно и в самом деле пренебречь сопротивлением воздуха.
Что же осталось? Осталось приравнять ускоряющий момент реактивной силы струи (1) тормозящему моменту силы трения Mtr:
Отсюда получим скорость истечения воды из трубки (в системе координат, связанной с огородом):
(как и предполагалось выше, ωl не превосходит скорости выброса воды относительно трубки).
А что дальше? А дальше, как говорят ученые, «проблема свелась к» известной школьной задаче о движении тела, брошенного под углом α к горизонту с начальной скоростью υ0 из точки с координатами (см. рис. 1)
Решение этой задачи дает
где t - время, прошедшее с момента выброса элементарной массы воды из трубки. Конечно, это решение предполагает, что элементы водяной струи или капли, образующиеся в результате дробления, никак не взаимодействуют друг с другом и с воздухом.
Для огорода очень важно, куда попадет вода и в каком количестве В принятой нами системе координат ордината почвы y = 0. Обозначим абсциссу точки падения воды через x↓. Исключая из последних двух уравнений время, получим
В частности, здесь содержится хорошо известное выражение для дальности полета, соответствующее случаю вылета из начала координат (h = 0, l = 0):
В этом случае наибольшая дальность полета достигается, как известно, при α = 45° и составляет
В общем же случае решение, как видно из выражения (2), зависит от двух параметров: отношения начальных значений потенциальной и кинетической энергии \(~a = \frac{gh}{\frac{\upsilon^2_0}{2}}\) и геометрического параметра нашего устройства — \(~\frac lh\). И Студент с увлечением принялся анализировать эти зависимости — тем более, что у него был компьютер.
Мы же ограничимся каким-нибудь характерным случаем. Например, предположим, что \(~\frac lh << 1\) (это означает, что вращающаяся трубка мала по сравнению с высотой ее над землей). Кроме того, предположим, что и дальность полета x0 max тоже много больше l, т.е. даже при выбросе воды с нулевой высоты она улетит достаточно далеко. Тогда абсцисса точки падения воды на почву, отнесенная к характерной величине (3), равна
Можно найти и угол вылета, соответствующий максимальной дальности, и величину самой этой дальности из условия равенства нулю производной:
откуда
Видно, что чем выше точка вылета, тем дальше сможет достать вода и тем меньше угол, при котором достигается эта наибольшая дальнобойность. Например, в случае a = 1 (начальные значения потенциальной и кинетической энергии одинаковы)
а дальность полета в \(~\sqrt 2\) раз больше, чем при вылете из точки на уровне земли (3).
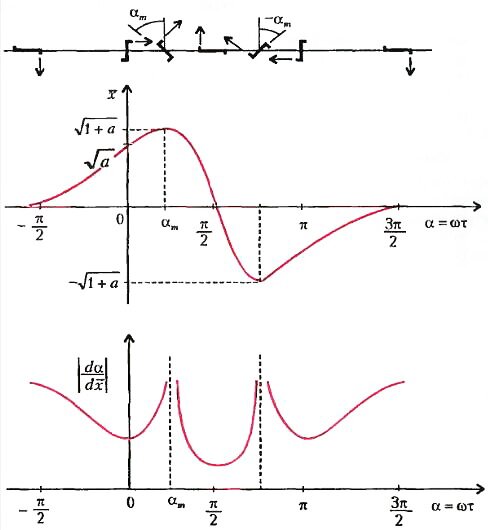
На рисунке 2 приведен качественный вид зависимости относительной координаты точки падения воды на почву от угла α (или от времени, поскольку α = ωt). В верхней части рисунка показаны положения вращающейся трубки, соответствующие нескольким характерным углам. Уже из этого графика видна неравномерность полива. В нижней части этого же рисунка построен график функции \(~|\frac{d \alpha}{d\bar x}|\), характеризующей плотность распределения воды по поверхности почвы. Действительно, при повороте на угол dα вода, выброшенная за соответствующий отрезок времени \(~dt = \frac{d \alpha}{\omega}\), попадает на участок dx (считаем, что она тут же поглощается почвой). Видно, что в некоторые моменты времени плотность полива обращается в бесконечность. И понятно почему - в эти моменты (при α = αm) струя воды, падающей на почву, на мгновение останавливается, меняя направление своего движения по поливаемой поверхности. А в изложенной теории струя считается бесконечно тонкой линией, несущей конечный расход воды.
«Но, - сказал себе Студент, - струя не линия, она уже на выходе из трубки имеет диаметр 2r0, а при дальнейшем движении еще может распадаться на капли, которые тормозятся в воздухе; и центробежная сила инерции может как-то изменить распределение давления по оси струи; и... следовательно, вся теория нуждается в проверке, доработке...» И много еще мыслей толпилось в голове Студента.
А что же огород? Спросите у бабушки...