Kvant. Сила и деформация
Кикоин А.К. Сила и деформация //Квант. — 1983. — № 12. — С. 25-27.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Слово «сила» — одно из наиболее употребляемых слов. В обыденном языке оно может иметь самые разные значения. Но в механике смысл этого слова вполне ясен. Все, что можно сказать о механической силе вообще, содержится в законах Ньютона.
В законе, числящемся под номером три, говорится, что сила, а точнее, силы возникают при взаимодействии тел. Из второго закона Ньютона следует, что сила — это причина ускорения тел, то есть изменения их скорости. Наконец, первый закон Ньютона утверждает, что при отсутствии сил или при равенстве нулю геометрической суммы приложенных к телу сил оно, тело, движется без ускорения. Все три закона сформулированы для случая, когда движение рассматривается относительно инерциальной системы отсчета.
Казалось бы, роль силы в механике ясна: сила сообщает телу, к которому она приложена, ускорение. Согласно законам механики, это ее единственная «специальность».
Между тем иногда встречаются (даже в учебниках физики) утверждения о том, что сила не только сообщает телу ускорение, но и деформирует его. В первом случае говорят о динамическом, а во втором — о статическом проявлении силы. Так, в одном из учебных пособий, рекомендованных старшеклассникам, читаем: «Результатом взаимодействия тел является либо деформация (изменение размеров или формы тела), либо ускорение (изменение величины или направления скорости). Конечно, не исключено, что одновременно могут возникать и деформации, и ускорения». Еще пример. В учебнике для высшей школы, пользующемся всемирной известностью, сила определяется следующими словами: «Понятие „сила” - происходит от нашего мускульного ощущения. Качественно сила определяется двумя признаками: она может деформировать неподвижное твердое тело и ускорять подвижное тело». В других книгах читаем: «Силой называется то, что вызывает или прекращает движение, изменяет направление движения или изменяет форму тела» или «сила - векторная величина, характеризующая взаимодействие тел, в результате которого тела деформируются или приобретают ускорения... Статическое действие силы проявляется в наличии деформаций, динамическое в наличии ускорений». Число таких примеров можно увеличить, хотя в большинстве современных книг по физике силу с деформацией непосредственно не связывают.
Как же, в самом деле, связаны между собой силы, ускорения и деформации?
Сила — причина ускорения.
Повторим еще раз, что в трех законах Ньютона, с помощью которых может быть решена любая механическая задача, нет и намека на такое явление, как деформация тел. Да и не может быть, потому что законы Ньютона относятся к движению материальных точек (это постоянно подчеркивается в учебнике «Физика 8»). А точки, разумеется, деформироваться не могут! Уже отсюда следует, что силу, в соответствии с законами Ньютона, следует рассматривать как причину ускорения и только ускорения.
Однако связь между силой и деформацией действительно существует. Прежде всего, она состоит в том, что одна из трех рассматриваемых в учебнике механических сил — сила упругости — возникает именно при деформации тел. Но ведь это означает, что сила (по крайней мере, сила упругости) есть следствие деформации. Как же тогда понимать приведенные выше утверждения о том, что сила — это причина деформации? Быть может, они просто не имеют смысла? Чтобы ответить на эти вопросы, вспомним
Как возникают деформации?
Деформации — это изменения формы или размеров тела. Они невозможны без изменения взаимного расположения частиц тела. При деформации растяжения, например, расстояния между частицами тела увеличиваются, частицы удаляются друг от друга. При сжатии тела его частицы, наоборот, сближаются. Таким образом, непосредственная причина деформации — это движения одних частиц тела относительно других. Движения, а не силы!
Но и силы играют существенную роль, потому что именно от них зависят те движения, которые приводят к деформации тела. Однако роль сил не прямая, а косвенная. Сила непосредственно не вызывает деформации.
И деформация, и ускорение.
Рассмотрим более подробно, каким образом сила, приложенная к телу, сообщает ему ускорение и какую роль при этом играет деформация.
Допустим, что к телу массой m, имеющему, например, форму стержня, приложена постоянная сила \(~\vec F\) так, как это показано на рисунке 1.
Оговорим только, что \(~\vec F\) — не сила всемирного тяготения. Поскольку сила приложена к правому торцу стержня, она непосредственно сообщит ускорение лишь точкам (частицам) на этом торце. Только они, эти точки, и получат ускорение в начальный момент времени. Остальные точки стержня останутся в покое, так как к ним сила не приложена. Благодаря этому стержень деформируется, возникает сила упругости, и она (а не сила \(~\vec F\)!) сообщает ускорение следующему слою точек и т. д. Постепенно, хотя и очень быстро (со скоростью звука), деформация распространится по всему стержню, в результате чего весь стержень станет двигаться с ускорением \(~\vec a\), равным \(~\frac{\vec F}{m}\).
Таким образом, в рассмотренном случае тело под действием приложенной к нему силы движется с ускорением и при этом оказывается деформированным. В том, что тело деформировано, «виновата», конечно, и сила \(~\vec F\), но ее роль не прямая. Тело оказалось деформированным, поскольку разные его точки двигались относительно друг друга. То, что роль силы при деформации лишь косвенная, видно уже из того, что величина и характер деформации не определяются однозначно приложенной силой, а зависят и от материала стержня, и от однородности его по сечению и составу. Ускорение же стержня однозначно определяется действующей на него силой.
Ускорение без деформации.
Важно отметить также, что сила, приложенная к телу, может и не вызвать деформацию. Если эта сила — сила тяжести (вообще, сила всемирного тяготения), то картина движения будет совсем иной. Силы тяжести, как известно, действуют сразу на все точки тела и сообщают им одно и то же ускорение \(~\vec g\). Поэтому все точки будут двигаться одинаково, так что движения одних точек относительно других не будет. Не будет, следовательно,и деформации.
Деформация без ускорения.
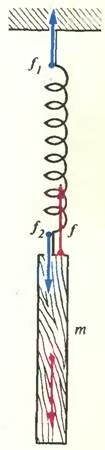
Рассмотрим теперь такой случай. К невесомой пружине, верхний конец которой прикреплен к неподвижной подставке, подвешивается тело массой m (рис. 2).
Под действием силы тяжести тело, конечно, начинает падать. Вместе с ним приходит в движение и нижний конец пружины. Поэтому пружина деформируется, и возникает сила упругости, действующая на верхний конец тела. Так как сила тяжести действует на все части тела, а сила упругости только на его верхний конец, различные части тела будут двигаться по-разному и тело окажется деформированным. Сила упругости, возникшая вследствие этого, будет действовать на нижний конец пружины и т. д.
Легко понять, что в конце концов и пружина, и тело остановятся. Это значит, что сумма сил, действующих и на пружину, и на тело, будет равна нулю. На пружину действует сила упругости со стороны деформированной подставки и сила упругости деформированного тела (силы \(~\vec f_1\), и \(~\vec f_2\) на рисунке 2). На тело действуют сила тяжести \(~m \vec g\) и сила упругости деформированной пружины \(~\vec f\). Все тела нашей системы деформированы, но ни одно из них не обладает ускорением.
Очевидно, именно эту ситуацию имеют в виду, когда говорят о статическом действии силы, то есть о действии силы, приводящем к деформации, но не ускорению (действительно, в нашем примере речь может идти об этом). Однако надо понимать, что в случаях, подобных рассмотренному, ускорения нет потому, что и на тело, и на пружину действуют две силы и их сумма равна нулю. Разумеется, ни при каких условиях одна сила (или несколько сил, если их сумма не равна нулю) не может деформировать тело, не сообщив ему и ускорения тоже. У силы (одной!) не может быть статического действия. Сила — величина динамическая.