Kvant. Слинки

Чокин Д. Слинки — шагающая пружинка //Квант. — 1991. — № 6. — С. 42-44.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

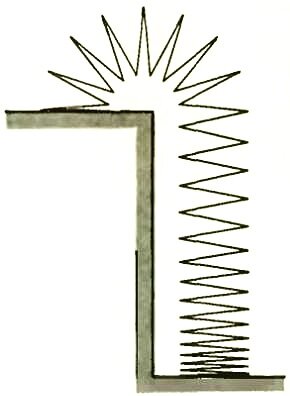
В этой статье будет рассказано об одной удивительной игрушке, которую в Америке называют слинки (slinky). Это пружинка с очень малым коэффициентом упругости, диаметр ее витков — от 5 до 10 см, количество витков — от 50 до 100. При всей внешней простоте такую пружинку трудно сделать самому. Нужна особая сталь, прошедшая специальную термообработку, только тогда можно добиться малой упругости пружинки. А именно это свойство и позволяет проводить с ней интересные опыты, которые невозможны с обычной пружинкой. Самое любопытное заключается в том, что слинки может спускаться по ступенькам лестницы (или по наклонной плоскости). Достаточно, установив слинки в вертикальном положении на краю ступеньки, подтолкнуть ее верхний конец в направлении нижней ступеньки, и слинки зашагает. Пружинка будет как бы перетекать с верхней ступеньки на нижнюю. Когда вся пружинка перетечет, верхний конец, описав в воздухе дугу, шагнет на следующую ступеньку, и движение продолжится (рис. 1).

Рис. 1

Попробуем объяснить этот опыт. Очевидно, главная причина в том, что, вследствие своей малой жесткости, пружинка не успевает погасить горизонтальную составляющую скорости своего верхнего конца, и это позволяет ей перешагнуть (перевалиться) на следующую ступеньку. Такую «шагающую» пружинку можно уподобить автоколебательной системе, черпающей кинетическую энергию из потенциальной. Оценим некоторые динамические параметры слинки: время одного шага, отношение массы пружинки, участвующей в движении, к ее полной массе и др. С этой целью решим следующую задачу.

Рис. 2

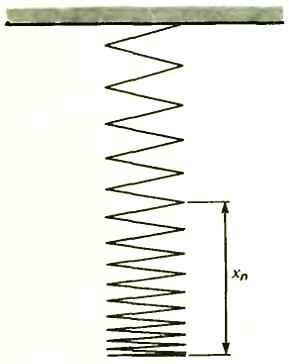
Свободно подвесим слинки за верхний конец (рис. 2) и найдем зависимость линейной плотности пружинки, что пропорционально числу витков на единицу длины, от расстояния до нижнего конца. Рассмотрим некоторый участок пружинки. Пусть он приходится на n-й виток, считая от нижнего конца пружинки. Если длина этого витка равна Δx_n, то

\(~\Delta k \Delta x_n = \Delta mng,\)

где Δk — жесткость одного витка, а Δm — его масса. Тогда получаем, что средняя линейная плотность n-го витка равна

\(~\lambda_n = \frac{\Delta m}{\Delta x_n} = \frac{\Delta k}{ng},\)

или, считая, что в пружинке N витков и ее общая жесткость k, —

\(~\lambda_n = \frac{Nk}{ng}.\)

Теперь найдем расстояние от этого витка до нижнего конца пружинки. Поскольку \(~\Delta x_n = \frac{\Delta mng}{\Delta k}\), искомое расстояние равно

\(~x_n = \sum^n_{i=1} \frac{\Delta mg}{\Delta k}i = \frac{\Delta mg}{\Delta k} \frac{n(n + 1)}{2} \approx \frac{\Delta mgn^2}{2\Delta k} = \frac{Mg}{2k} \frac{n^2}{N^2},\)

где М — масса всей пружинки. (Интересно, что полная длина подвешенной пружины \(~L_0 = \frac{Mg}{2k}\) оказывается в два раза меньше длины, которую имела бы такая же невесомая пружина с подвешенным на конце грузом массой М.)

Сравнив полученные выражения для линейной плотности λ_n и расстояния x_n, найдем зависимость между ними:

\(~\lambda_n = \frac{k}{g} \frac{N}{n} = \sqrt{\frac{Mk}{2gx_n}}.\)

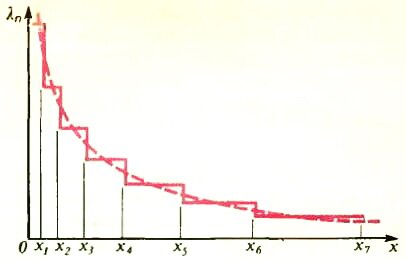
Для удобства (нам это понадобится в дальнейшем) перейдем от дискретной записи распределения линейной плотности к непрерывной, взяв предельный случай бесконечного количества витков (см. рис. 3):

\(~\lambda(x) = \sqrt{\frac{Mk}{2gx}}.\)

Рис. 3

Теперь настало время оценить массу пружинки, участвующую в движении. Будем считать, что искомая часть эквивалентна свободно подвешенной пружинке, длина которой h (h — высота ступеньки). Тогда, используя последнюю формулу, оценим неизвестную массу:

\(~m_0 = \int^h_0 \lambda(x)dx = \int^h_0 \sqrt{\frac{Mk}{2gx}}dx = \sqrt{\frac{2Mkh}{g}}\)

и отношение этой массы к полной:

\(~\frac{m_0}{M} = \sqrt{\frac{2kh}{Mg}} = \sqrt{\frac{h}{L_0}}.\)

Чем меньшая часть массы пружинки будет участвовать в движении, тем устойчивее она будет ходить. Поэтому для улучшения ходьбы пружинки следует, как видно из полученного отношения, уменьшить коэффициент упругости, увеличить массу пружинки, пускать пружинку с не очень высоких ступенек. И вообще, лучше делать это, скажем, на Юпитере — с целью увеличения ускорения свободного падения g. Для реальной пружинки, взяв h = 10 см и L₀ = 1 м, получим \(~\frac{m_0}{M} \approx 0,3\).

Чтобы определить время одного шага слинки, воспользуемся вторым законом Ньютона. Пусть начальная скорость верхнего витка υ. Тогда

\(~\upsilon \Delta m = F \Delta t,\)

где F — сила натяжения пружинки в верхней точке, Δm — масса пружинки, которая пришла в движение за время Δt. Если λ₀ — линейная плотность пружинки в месте начала движения, то \(~\Delta m = \lambda_0 \upsilon \Delta t\), и

\(~\lambda_0 \upsilon^2 = F.\)

Очевидно, что

\(~\lambda_0 = \sqrt{\frac{Mk}{2gh}}\), а \(~F = m_0g = \sqrt{2Mgkh}.\)

Поэтому для скорости «разматывания» получаем

\(~\upsilon = \sqrt{\frac{F}{\lambda_0}} = \sqrt{2gh}.\)

Пусть за время Δt «размоталась» часть пружинки массой \(~\Delta m = \lambda_0 \upsilon \Delta t\). Подставив значения λ₀ и υ, имеем

\(~\Delta t = \frac{\Delta m}{\sqrt{Mk}}.\)

Откуда получаем время одного шага слинки:

\(~T = \sum \Delta t_i = \frac{1}{\sqrt{Mk}} \sum \Delta m_i = \sqrt{\frac{M}{k}} = \sqrt{\frac{2L_0}{g}}.\)

Интересно, что время одного шага не зависит от высоты ступеньки и что это время одного порядка с периодом свободных колебаний пружинки и со временем падения тела с высоты L₀. Взяв значение L₀ равным, например, 1 м, получим T ~ 0,5 с, что хорошо подтверждается экспериментом.

Другой, не менее важный опыт с пружинкой — моделирование продольных механических волн. Для проведения этого опыта необходимо растянуть пружинку и один из ее витков сжать вдоль оси, тем самым сделав его началом распространения волны. По пружинке побежит волна сжатия и растяжения, отражаясь от ее концов. Интересный и полезный опыт. Его можно показывать в школе для наглядного представления продольных волн и исследования их свойств. Например, известно, что уменьшение плотности среды ведет к увеличению скорости продольных волн. В этом легко убедиться в опытах со слинки — достаточно немного ее растянуть, чтобы скорость волн заметно увеличилась.

Наверное, много еще интересных опытов можно провести с пружинкой, обладающей очень малой жесткостью, т. е. со слинки.