Kvant. Солнце, лампа и кометы

Стасенко А.Л. Солнце, лампа и кометы //Квант. — 1996. — № 1. — С. 40-41.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Ну кто же не знает, что нагретые тела излучают тепло, а очень нагретые еще и светятся? В этом легко убедиться, включив утюг, став у костра или взглянув на Солнце. Интуитивно ясно, что чем выше температура нагретого тела, тем больше энергии оно будет излучать в единицу времени с единицы своей поверхности. Но как зависит эта величина, называемая плотностью потока энергии, от температуры? Тут нам очень помогут соображения размерностей.

Итак, нужно найти зависимость плотности потока энергии q, размерность которой Дж / (с·м²), от температуры Т. Поскольку в основе самого процесса нагревания тела лежит тепловое движение его частиц, то температура должна входить вместе с множителем k, называемым постоянной Больцмана, т.е. в виде произведения kT. Далее, так как процесс излучения есть принципиально квантовое явление, то не обойтись без постоянной Планка h (это самая любимая константа в журнале «Квант»), а поскольку излучение представляет собой электромагнитную волну, то должна войти и скорость света с. Теперь воспользуемся методом размерностей и будем искать зависимость вида

\(~q \sim (kT)^n h^m c^p\) ,

или, подставив вместо каждой из величин ее размерность,

Дж / (с·м²) = Джⁿ · (Дж·с)^m · (м/с)^p .

Для определения показателей степени n, m и p приравняем степени одинаковых размерностей справа и слева и получим три уравнения с тремя неизвестными:

\(~\begin{matrix} 1 = n + m \\ -1 = m - p \\ -2 = p \end{matrix}\) .

Отсюда легко найдем

\(~\begin{matrix} p = -2 \\ m = -3 \\ n = 4 \end{matrix}\) .

Таким образом,

\(~q \sim \frac{(kT)^4}{h^3 c^2} = aT^4\) ,

где a — постоянная величина. Это так называемый закон Стефана — Больцмана.

Оценим постоянный множитель a, содержащий фундаментальные константы физики k = 1,38·10^-23 Дж/К, h = 6·10^-34 Дж·с, с = 3·10⁸ м/с (полюбуйтесь степенями — не каждый день такое увидишь!):

\(~a = \frac{k^4}{h^3 c^2}\) = 1,8·10^-9 Дж/(с·м²·K⁴) .

Точное значение постоянного множителя при Т⁴ равно

σ = 5,67·10^-8 Дж/(с·м²·K⁴) .

Да, мы ошиблись на порядок — но ведь и степени нешуточные. Впрочем, для дальнейшего нам достаточен лишь факт пропорциональности \(~q \sim T^4\).

Рис. 1

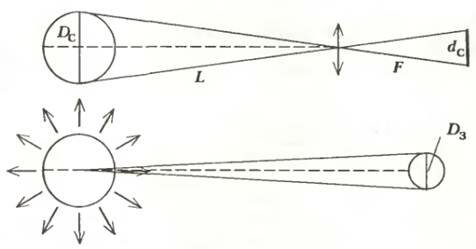
Закон Стефана — Больцмана очень полезный закон. Например, с его помощью можно оценить температуру «поверхности» Солнца, даже не погружая в него термометр. Надо лишь знать среднюю температуру Земли T_z и определить угловой диаметр диска Солнца α_c, что легко сделать при помощи положительной линзы (рис.1). Измерив D_c и F (фокусное расстояние), получим α_c ≈ D_c / F ≈ 0,5 градуса ≈ 10^-2 радиана. Теперь запишем тот факт, что Земля заметно не нагревается и не охлаждается, по крайней мере в течение нашей жизни (имеется в виду средняя по поверхности температура T_z ≈ 300 К). Значит, тепло Солнца, поглощенное Землей, переизлучается ею же в космос. Если искомая температура Солнца T_c, то в единицу времени вся его поверхность излучает во всех направлениях энергию \(~\sigma T^4_c \pi D^2_c\). Земля получает только часть этой энергии, равную отношению ее диаметрального сечения \(~\frac{\pi D^2_z}{4}\) к площади \(~4 \pi L^2\) сферы с радиусом L, равным расстоянию между Землей и Солнцем. Вся эта энергия тут же излучается поверхностью Земли (хотя она и не раскалена и не светится) при ее температуре T_z. Итак,

\(~\sigma T^4_c \pi D^2_c \frac{\frac{\pi D^2_z}{4}}{4 \pi L^2} = \sigma T^4_z \pi D^2_z\) ,

откуда

\(~T_c = T_z \sqrt[4]{16 \left( \frac{L}{D_c} \right)^2}\) .

Но ведь D_c / L ≈ α_c ≈ 10^-2 рад (см. рис.1), так что

\(~T_c = 300 \sqrt[4]{\frac{16}{10^{-4}}} K = 6000 K\) .

А зная температуру Солнца, можно оценить равновесные температуры других планет: Меркурия, Венеры, Марса, ... и даже гипотетического пояса Оорта, являющегося, по предположению, банком комет, прилетающих в Солнечную систему. Для этого нужно только знать, во сколько раз дальше (или ближе) от Солнца расположена эта планета. Например, считая пояс Оорта отстоящим в 20000 раз дальше, чем Земля, получим равновесную температуру комет: T_k ~ 2К — всего два градуса по шкале Кельвина! Ну это уж слишком мало — ведь вся Вселенная пронизана реликтовым равновесным излучением с температурой порядка 3 К, оставшимся от первородного взрыва. Значит, нужно учесть и приток к кометам энергии этого излучения.

Рис. 2

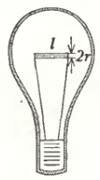
Но вернемся на Землю. При помощи закона Стефана — Больцмана можно, например, узнать, как остывает нить накала вакуумной лампочки (рис.2). Считая эту нить цилиндром радиусом r и длиной l, запишем закон изменения ее температуры со временем в виде

\(~d(CT) = -2 \pi rl \sigma T^4 dt\) ,

где С — теплоемкость нити, а знак «минус» означает потерю ее теплосодержания СТ. Если в момент отключения (t = 0) температура была T₀, то

\(~\frac{dT}{T^4} = -\frac 13 d \left(\frac{1}{T^3}\right) = -\frac{2 \pi rl \sigma}{C} dt\) ,

или (считая С постоянной)

\(~\frac{1}{T^3} - \frac{1}{T^3_0} = \frac{6 \pi rl \sigma}{C} t\) .

Окончательно

\(~T = \frac{T_0}{\sqrt[3]{1 + \frac{6 \pi rl \sigma T^3_0}{C} t}}\) .

Отсюда можно найти такое время, за которое температура упадет, скажем, в два, три, четыре... раза (значит, излучаемая энергия — в 16, 81, 256... раз соответственно), так что лампочка перестанет быть видимой в темноте. (Попробуйте самостоятельно провести такие оценки.)

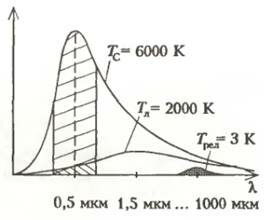
Тут самое время вспомнить, что, согласно закону Планка, в излучении нагретого тела присутствуют электромагнитные волны всех длин. Наш глаз видит в так называемом оптическом диапазоне — от 0,4 до 0,7 мкм. На рисунке 3 приведен качественный вид распределения энергии в спектре равновесного излучения абсолютно черного тела при температурах T_c = 6000 К и T_l = 2000 К, характерных для поверхности Солнца и лампочки накаливания. Максимум кривой Планка для Солнца соответствует длине волны λ_m ≈ 0,5 мкм, лежащей внутри оптического диапазона, что не удивительно: Природа за миллионы лет приспособила наши глаза именно к солнечному свету. Для лампы накаливания λ_m ≈ 1,5 мкм, значит, основная часть ее излучения лежит в инфракрасной области спектра, так что эта лампа представляет собой скорее нагревательный прибор, чем осветительный. Кстати, отношение площадей под этими кривыми равно \(~\left(\frac{T_c}{T_l} \right)^4 = 3^4 = 81\), согласно тому самому закону Стефана — Больцмана, с которого мы начали.

Это потому, что площадь под каждой кривой и есть мощность излучения единицы поверхности тела во всем диапазоне длин волн от 0 до \(~\infty\).

Рис. 3

А что там еще за бугорок (см. рис.3) в окрестности длины волны 1000 мкм, т.е. миллиметра? Это — спектральное распределение энергии реликтового излучения с температурой около 3 К.

В заключение посмотрим еще раз на рисунок 3 и сделаем еще одно интересное наблюдение. Умножим значения длин волн, соответствующие максимумам кривой Планка, на температуры, при которых построена каждая из этих кривых: 0,5 мкм·6000 К — для Солнца, 1,5 мкм·2000 К — для лампы накаливания, 1000 мкм·3 К — для реликтового излучения. Получим одно и то же число. Возникает подозрение, что тут скрыт какой-то закон. Это подозрение еще раньше нас закралось в голову Вина, поэтому только что открытый закон уже носит его имя.