Referat. Свет как волна

Свет как электромагнитная волна

Природа света

Первые представления о природе света возникли у древних греков и египтян. По мере изобретения и совершенствования различных оптических приборов (параболических зеркал, микроскопа, зрительной трубы) эти представления развивались и трансформировались. В конце XVII века возникли две теории света: корпускулярная (И. Ньютон) и волновая (Р. Гук и Х. Гюйгенс).

Волновая теория рассматривала свет как волновой процесс, подобный механическим волнам. В основу волновой теории был положен принцип Гюйгенса. Большая заслуга в развитии волновой теорий принадлежит английскому физику Т. Юнгу и французскому физику О. Френелю, исследовавшим явления интерференции и дифракции. Исчерпывающее объяснение этих явлений могло быть дано только на основе волновой теории. Важное экспериментальное подтверждение справедливости волновой теории было получено в 1851 году, когда Ж. Фуко (и независимо от него А. Физо) измерил скорость распространения света в воде и получил значение υ < c.

Хотя к середине XIX века волновая теория была общепризнана, вопрос о природе световых волн оставался нерешенным.

В 60-е годы XIX века Максвеллом были установлены общие законы электромагнитного поля, которые привели его к заключению, что свет – это электромагнитные волны. Важным подтверждением такой точки зрения послужило совпадение скорости света в вакууме с электродинамической постоянной:

\(~c = \dfrac{1}{\sqrt{\varepsilon_0 \mu_0}}\) .

Электромагнитная природа света получила признание после опытов Г. Герца (1887–1888 гг.) по исследованию электромагнитных волн. В начале XX века после опытов П. Н. Лебедева по измерению светового давления (1901 г.) электромагнитная теория света превратилась в твердо установленный факт.

Важнейшую роль в выяснении природы света сыграло опытное определение его скорости. Начиная с конца XVII века предпринимались неоднократные попытки измерения скорости света различными методами (астрономический метод А. Физо, метод А. Майкельсона). Современная лазерная техника позволяет измерять скорость света с очень высокой точностью на основе независимых измерений длины волны λ и частоты света ν (c = λ · ν). Таким путем было найдено значение c = 299792458 ± 1,2 м/с превосходящее по точности все ранее полученные значения более чем на два порядка.

Свет играет чрезвычайно важную роль в нашей жизни. Подавляющее количество информации об окружающем мире человек получает с помощью света. Однако в оптике как разделе физике под светом понимают не только видимый свет, но и примыкающие к нему широкие диапазоны спектра электромагнитного излучения – инфракрасный (ИК) и ультрафиолетовый (УФ). По своим физическим свойством свет принципиально неотличим от электромагнитного излучения других диапазонов – различные участки спектра отличаются друг от друга только длиной волны λ и частотой ν.

Для измерения длин волн в оптическом диапазоне используются единицы длины 1 нанометр (нм) и 1 микрометр (мкм):

1 нм = 10^-9 м = 10^-7 см = 10^-3 мкм.

Видимый свет занимает диапазон приблизительно от 400 нм до 780 нм или от 0,40 мкм до 0,78 мкм.

Распространяющееся в пространстве периодически изменяющееся электромагнитное поле и представляет собой электромагнитную волну.

Наиболее существенные свойства света как электромагнитной волны

1. При распространении света в каждой точке пространства происходят периодически повторяющиеся изменения электрического и магнитного полей. Эти изменения удобно изображать в виде колебаний векторов напряженности электрического поля \(~\vec E\) и индукции магнитного поля \(~\vec B\) в каждой точке пространства. Свет — поперечная волна, так как \(~\vec E \perp \vec \upsilon\) и \(~\vec B \perp \vec \upsilon\) .
2. Колебания векторов \(~\vec E\) и \(~\vec B\) в каждой точке электромагнитной волны происходят в одинаковы фазах и по двум взаимно перпендикулярным направлениям \(~\vec E \perp \vec B\) в каждой точке пространства.
3. Период света как электромагнитной волны (частота) равен периоду (частоте) колебаний источника электромагнитных волн. Для электромагнитных волн справедливо соотношение \(~\lambda = \upsilon \cdot T = \dfrac{\upsilon}{\nu}\) . В вакууме \(~\lambda_0 = c \cdot T = \dfrac{c}{\nu}\) – длина волны наибольшая по сравнению с λ в другой среде, так как ν = const и изменяется только υ и λ при переходе от одной среды к другой.
4. Свет является носителем энергии, причем перенос энергии совершается в направлении распространения волны. Объемная плотность энергии электромагнитной поля определяется выражением \(~\omega_{em} = \dfrac{\varepsilon \cdot \varepsilon_0 \cdot E^2}{2} + \dfrac{B^2}{2 \cdot \mu \cdot \mu_0}\)
5. Свет, как и другие волны, распространяются прямолинейно в однородной среде, испытывают преломление при переходе из одной среды во вторую, отражаются от металлических преград. Для них характерны явления дифракции и интерференции.

Интерференция света

Для наблюдений интерференции волн на поверхности воды использовались два источника волн (два шарика, закрепленные на колеблющемся стерженьке). Получить интерференционную картину (чередование минимумов и максимумов освещенности) с помощью двух обычных независимых источников света, например двух электрических лампочек, невозможно. Включение еще одной лампочки лишь увеличивает освещенность поверхности, но не создает чередования минимумов и максимумов освещенности.

Для того чтобы при наложении световых волн наблюдалась устойчивая интерференционная картина, необходимо, чтобы волны были когерентны, т. е. имели одинаковую длину волны и постоянную разность фаз.

Почему световые волны от двух источников не когерентны?

Интерференционная картина от двух источников, которую мы описали, возникает только при сложении монохроматических волн одинаковых частот. У монохроматических волн разность фаз колебаний в любой точке пространства постоянна.

Волны с одинаковой частотой и постоянной разностью фаз называются когерентными.

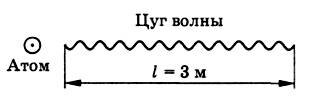
Только когерентные волны, налагаясь друг на друга, дают устойчивую интерференционную картину с неизменным расположением в пространстве максимумов и минимумов колебаний. Световые же волны от двух независи-мых источников не являются когерентными. Атомы источников излучают свет независимо друг от друга отдельными «обрывками» (цугами) синусоидальных волн. Длительность непрерывного излучения атома около 10 с. За это время свет проходит путь длиной около 3 м (рис. 1).

Рис. 1

Эти цуги волн от обоих источников налагаются друг на друга. Разность фаз колебаний в любой точке пространства хаотически меняется со временем в зависимости от того, как в данный момент времени цуги от различных источников сдвинуты друг относительно друга. Волны от различных источников света некогерентны из-за того, что разность начальных фаз не остается постоянной. Фазы φ₀₁ и φ₀₂ меняются случайным образом, и из-за этого случайным образом меняется разность фаз результирующих колебаний в любой точке пространства.

При случайных обрывах и возникновениях колебаний разность фаз меняется беспорядочно, принимая за время наблюдения τ всевозможные значения от 0 до 2π. В результате за время τ много большее времени нерегулярных изменений фазы (порядка 10^-8 с), среднее значение cos (φ₁ – φ₂) в формуле

\(~I = 4 I_0 \cos^2 \dfrac{\varphi_1 - \varphi_2}{2} = 2 I_0 [1 + \cos (\varphi_1 - \varphi_2)]\) .

равно нулю. Интенсивность света оказывается равной сумме интенсивностей от отдельных источников, и никакой интерференционной картины наблюдаться не будет. В некогерентности световых волн заключается главная причина того, что свет от двух источников не дает интерференционной картины. Это главная, но не единственная причина. Другая причина заключается в том, что длина световой волны, как мы скоро увидим, очень мала. Это сильно затрудняет наблюдение интерференции, если даже располагать когерентными источниками волн.

Условия максимумов и минимумов интерференционной картины

В результате наложения двух или более когерентных волн в пространстве возникает интерференционная картина, представляющая собой чередование максимумов и минимумов интенсивности света, а значит, и освещенности экрана.

Интенсивность света в данной точке пространства определяется разностью фаз колебаний φ₁ – φ₂. Если колебания источников синфазны, то φ₀₁ – φ₀₂ = 0 и

\(~\Delta \varphi = \varphi_1 - \varphi_2 = 2 \pi \dfrac{r_2 - r_1}{\lambda}\) . (1)

Разность фаз определяется разностью расстояний от источников до точки наблюдения Δr = r₁ – r₂ (разность расстояний называется разностью хода). В тех точках пространства, для которых выполняется условие

\(~\Delta r = r_1 - r_2 = k \lambda ; k = 0, 1, 2, \ldots\) . (2)

волны, складываясь, усиливают друг друга, и результирующая интенсивность в 4 раза превосходит интенсивность каждой из волн, т.е. наблюдается максимум. Напротив, при

\(~\Delta r = r_1 - r_2 = \dfrac{\lambda}{2} (2k + 1)\) . (3)

волны гасят друг друга (I = 0), т.е. наблюдается минимум.

Принцип Гюйгенса – Френеля

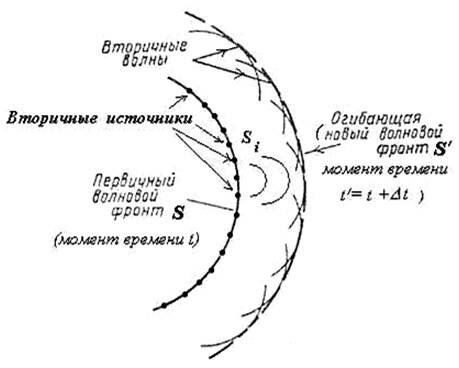
Волновая теория основывается на принципе Гюйгенса: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени.

Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис. 2). Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в однородной изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т. е. волна огибает края отверстия.

Рис. 2

Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, объясняет явление дифракции, но не затрагивает вопроса об амплитуде, а, следовательно, и об интенсивности волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.

Согласно принципу Гюйгенса – Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками.

Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн. Френель исключил возможность возникновения обратных вторичных волн и предположил, что если между источником и точкой наблюдения находится непрозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии – такая же, как при отсутствии экрана. Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства, т. е. определить закономерности распространения света.

Способы получения интерференционной картины

Идея Огюстена Френеля

Для получения когерентных источников света французский физик Огю-стен Френель (1788—1827) нашел в 1815 г. простой и остроумный способ. Надо свет от одного источника разделить на два пучка и, заставив их пройти различные пути, свести вместе. Тогда цуг волн, испущенных отдельным атомом, разделится на два когерентных цуга. Так будет для цугов волн, испускаемых каждым атомом источника. Свет, испускаемый одним атомом, дает определенную интерференционную картину. При наложении этих картин друг на друга получается достаточно интенсивное распределение освещенности на экране: интерференционную картину можно наблюдать.

Имеется много способов получения когерентных источников света, но суть их одинакова. С помощью разделения пучка на две части получают два мнимых источника света, дающих когерентные волны. Для этого используют два зеркала (бизеркала Френеля), бипризму (две призмы, сложенные основаниями), билинзу (разрезанную пополам линзу с раздвинутыми половинами) и др.

Кольца Ньютона

Первый эксперимент по наблюдение интерференции света в лаборатор-ных условиях принадлежит И. Ньютону. Он наблюдал интерференционную картину, возникающую при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны. Интерференционная картина имела вид концентрических колец, получивших название колец Ньютона (рис. 3 а, б).

Рис. 3 а

Рис. 3 б

Ньютон не смог объяснить с точки зрения корпускулярной теории, почему возникают кольца, однако он понимал, что это связано с какой-то периодичностью световых процессов.

Опыт Юнга с двумя щелями

Предложенный Т. Юнгом эксперимент убедительно демонстрирует волновую природу света. Для лучшего понимания результатов опыта Юнга полезно сначала рассмотреть ситуацию, когда свет проходит через одну щель в перегородке. В опыте с одной щелью монохроматический свет от источника проходит через узкую щель и регистрируется на экране. Неожиданным является то, что при достаточно узкой щели на экране видна не узкая светящаяся полоска (изображение щели), а плавное распределение интенсивности света, имеющее максимум в центре и постепенно убывающее к краям. Это явление обусловлено дифракцией света на щели и также есть следствие волновой природы света.

Пусть теперь в перегородке сделаны две щели (рис. 4). Последовательно закрывая то одну, то другую щель, можно убедиться, что картина распределения интенсивности на экране будет такой же, как и в случае одной щели, но только положение максимума интенсивности будет каждый раз соответствовать положению открытой щели. Если же открыть обе щели, то на экране возникает чередующаяся последовательность светлых и темных полос, причем яркость светлых полос убывает с расстоянием от центра.

Рис. 4

Некоторые применения интерференции

Применения интерференции очень важны и обширны.

Существуют специальные приборы — интерферометры — действие которых основано на явлении интерференции. Назначение их может быть различным: точное измерение длин световых волн, измерение показателя преломления газов и др. Имеются интерферометры специального назначения. Об одном из них, сконструированном Майкельсоном для фиксации очень малых изменений скорости света, будет рассказано в главе «Основы теории относительности».

Мы остановимся только на двух применениях интерференции.

Проверка качества обработки поверхностей

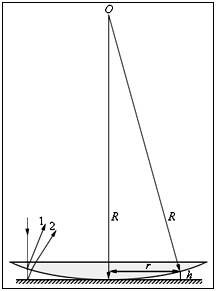
С помощью интерференции можно оценить качество шлифовки поверхности изделия с погрешностью до 10^-6 см. Для этого нужно создать тонкую прослойку воздуха между поверхностью образца и очень гладкой эталонной пластиной (рис. 5).

Рис. 5

Тогда неровности поверхности до 10^-6 см вызовут заметные искривления интерференционных полос, образующихся при отражении света от проверяемой поверхности и нижней грани эталонной пластины.

В частности, качество шлифовки линзы можно проверить, наблюдая кольца Ньютона. Кольца будут правильными окружностями только в том случае, если поверхность линзы строго сферическая. Любое отступление от сферичности, большее 0,1λ будет заметно сказываться на форме колец. В том месте, где на линзе имеется выпуклость, кольца будут выгибаться к центру.

Любопытно, что итальянский физик Э. Торричелли (1608— 1647) умел шлифовать линзы с погрешностью до 10^-6 см. Его линзы хранятся в музее, и качество их проверено современными методами. Как же это ему удавалось? Ответить на этот вопрос трудно. В то время секреты мастерства обычно не выдавались. Видимо, Торричелли обнаружил интерференционные кольца задолго до Ньютона и догадался, что с их помощью можно проверять качество шлифовки. Но, разумеется, никакого представления о том, почему кольца появляются, у Торричелли быть не могло.

Отметим еще, что, используя почти строго монохроматический свет, можно наблюдать интерференционную картину при отражении от плоскостей, находящихся друг от друга на большом расстоянии (порядка нескольких метров). Это позволяет измерять расстояния в сотни сантиметров с погрешностью до 10^-6 см.

Просветление оптики

Объективы современных фотоаппаратов или кинопроекторов, перископы подводных лодок и различные другие оптические устройства состоят из большого числа оптических стекол — линз, призм и др. Проходя через такие устройства, свет отражается от многих поверхностей. Число отражающих поверхностей в современных фотообъективах превышает 10, а в перископах подводных лодок доходит до 40. При падении света перпендикулярно поверхности от каждой поверхности отражается 5-9% всей энергии. Поэтому сквозь прибор часто проходит всего 10-20% поступающего в него света. В результате этого освещенность изображения получается малой. Кроме того, ухудшается качество изображения. Часть светового пучка после многократного отражения от внутренних поверхностей все же проходит через оптический прибор, но рассеивается и уже не участвует в создании четкого изображения. На фотографических изображениях, например, по этой причине образуется «вуаль».

Для устранения этих неприятных последствий отражения света от поверхностей оптических стекол надо уменьшить долю отраженной энергии света. Даваемое прибором изображение делается при этом ярче, «просветляется». Отсюда и происходит термин просветление оптики.

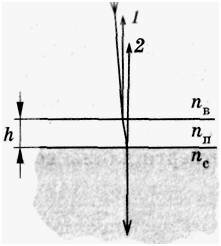
Просветление оптики основано на интерференции. На поверхность оптического стекла, например линзы, наносят тонкую пленку с показателем преломления n_n, меньшим показателя преломления стекла n_с. Для простоты рассмотрим случай нормального падения света на пленку (рис. 6).

Рис. 6

Условие того, что отраженные от верхней и нижней поверхностей пленки волны гасят друг друга, запишется (для пленки минимальной толщины) следующим образом:

\(~2h = \dfrac{\lambda}{2 n_n}\) . (4)

где \(~\dfrac{\lambda}{n_n}\) — длина волны в пленке, а 2h — разность хода.

Если амплитуды обеих отраженных волн одинаковы или очень близки друг к другу, то гашение света будет полным. Чтобы добиться этого, подбирают соответствующим образом показатель преломления пленки, так как интенсивность отраженного света определяется отношением коэффициентов преломления двух граничащих сред.

На линзу при обычных условиях падает белый свет. Выражение (4) показывает, что требуемая толщина пленки зависит от длины волны. Поэтому осуществить гашение отраженных волн всех частот невозможно. Толщину пленки подбирают так, чтобы полное гашение при нормальном падении имело место для длин волн средней части спектра (зеленый цвет, λ_з = 5,5·10^-7 м); она должна быть равна четверти длины волны в пленке:

\(~h = \dfrac{\lambda}{4 n_n}\) . (4)

Отражение света крайних участков спектра — красного и фиолетового — ослабляется незначительно. Поэтому объектив с просветленной оптикой в отраженном свете имеет сиреневый оттенок. Сейчас даже простые дешевые фотоаппараты имеют просветленную оптику. В заключение еще раз подчеркнем, что гашение света светом не означает превращения световой энергии в другие формы. Как и при интерференции механических волн, гашение волн друг другом в данном участке пространства означает, что световая энергия сюда просто не поступает. Гашение отраженных волн у объектива с просветленной оптикой означает, что весь свет проходит сквозь объектив.

Приложение

Сложение двух монохроматических волн

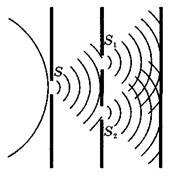
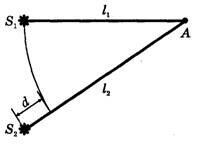
Рассмотрим более детально сложение двух гармонических волн одинаковой частоты ν в некоторой точке А однородной среды, считая, что источники этих волн S₁ и S₂ находятся от точки А на расстояниях, соответственно, l₁ и l₂ (рис. 7).

Рис. 7

Предположим для простоты, что рассматриваемые волны — либо продольные, либо перечные плоско поляризованные, а их амплитуды равны a₁ и a₂. Тогда, в соответствии с \(~x(s,t) = a \cdot \sin (\omega t - k s + \varphi_0)\) , уравнения этих волн в точке А имеют вид

\(~x_1(l_1,t) = a_1 \cdot \sin (\omega t - k l_1 + \varphi_{01})\) . (5) \(~x_2(l_2,t) = a_2 \cdot \sin (\omega t - k l_2 + \varphi_{02})\) . (6)

Уравнение результирующей волны, являющейся суперпозицией волн (5), (6), представляет собой их сумму:

\(~x(t) = x_1(l_1,t) + x_2(l_2,t) = a \cdot \sin (\omega t + \varphi)\) , (7)

причем, как можно доказать, используя известную из геометрии теорему косинусов, квадрат амплитуды результирующего колебания определяется формулой

\(~a^2 = a^2_1 + a^2_2 + 2 a_1 a_2 \cos \Delta \varphi\)> , (8)

где Δφ — разность фаз колебаний:

\(~\Delta \varphi = k(l_1 - l_2) - (\varphi_{01} - \varphi_{02})\) . (9)

(Выражение для начальной фазы φ₀₁ результирующего колебания мы приводить не будем из-за его громоздкости).

Из (8) видно, что амплитуда результирующего колебания является периодической функцией разности хода Δl. Если разность хода волн такова, что разность фаз Δφ равна

\(~\Delta \varphi = \pm 2 \pi n ; n = 0, 1, 2, \ldots\) , (10)

то в точке А амплитуда результирующей волны будет максимальной (условие максимума), если же

\(~\Delta \varphi = \pm (2n +1) \pi\) , (11)

то амплитуда в точке А минимальна (условие минимума).

Считая для простоты, что φ₀₁ = φ₀₂ и a₁ = a₂ , и учитывая равенство \(~k = \dfrac{\omega}{\upsilon} = \dfrac{2 \pi}{\lambda}\) , условия (10) и (11) и соответствующие выражения для амплитуды а можно записать в виде:

\(~\Delta l = \pm n \lambda\) (условие максимума), (12)

и тогда а = a₁ + a₂ , и

\(~\Delta l = \pm (2n +1) \dfrac{\lambda}{2}\) (условие минимума), (13)

и тогда a = 0.

Литературы

1. Мякишев Г.Я. Физика: Оптика. Квантовая физика. 11 кл.: Учеб. для углубленного изучения физики / Г.Я. Мякишев, А.З. Синяков. – М.: Дрофа, 2002. – 464 с.
2. Буров Л.И., Стрельченя В.М. Физика от А до Я: учащимся, абитуриентам, репетиторам. – Мн.: Парадокс, 2000. – 560 с.

Составители

Сакович М., Бек В. (11 «А»), Максимкова А. (11 «В»)