Слободянюк А.И. Физика 10/19.4.II

Содержание книги

Предыдующая страница

§19. Волновые процессы

19.4 Интерференция волн.

19.4.2 Интерференция волн от нескольких точечных источников.

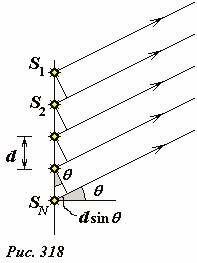
Рассмотрим физические принципы работы упомянутой фазовой решетки. Для этого рассчитаем результат интерференции волн, испущенных рядом точечных источников S₁, S₂,...S_N, расположенных на одной прямой и на равном расстоянии d друг от друга (Рис. 318). Каждый источник испускает сферические волны, одинаковой частоты, которые интерферируют во всем пространстве. Наша задача заключается в расчете амплитуды результирующей волны в некоторой точке, находящейся на очень большом расстоянии от источников (на рисунке не показана, так как находится очень далеко; зато лучи проведенные от источников до этой точки практически параллельны). Обозначим угол θ между направлением на эту точку и нормалью к системе источников. Опять мы рассматриваем задачу описания «интерференции параллельных лучей» - то есть, используем приближение, в котором разность хода от двух соседних источников до точки наблюдения описывается формулой

\(~\Delta r = d \sin \theta\) . (1)

Для управления направления максимума излучения между колебаниями двух соседних источников задается регулируемая разность фаз, которую мы обозначим φ₀. Волны, приходящие в точку наблюдения приобретают дополнительную разность фаз, обусловленную разностью расстояний (1). Поэтому между волнами, испущенными двумя соседними источниками, в рассматриваемой точке существует разность фаз, равная

\(~\Delta \varphi = \varphi_0 + \frac{2 \pi}{\lambda} \Delta r = \varphi_0 + \frac{2 \pi}{\lambda} d \sin \theta\) . (2)

Учитывая, что эта разность фаз одинакова для всех пар соседних источников, колебание, создаваемое источником номер n (n = 1,2..N) в точке наблюдения описывается формулой

\(~u_n = a \cos (\omega t - n \Delta \varphi)\) , (3)

где a - амплитуда этой волны в точке наблюдения. Таким образом, результирующее колебание описывается функцией, которая выражается следующей суммой

\(~U(t) = \sum_{n=1}^N a \cos (\omega t - n \Delta \varphi)\) . (4)

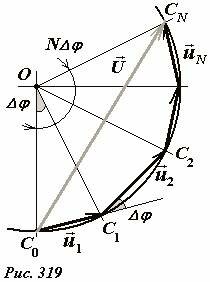
Для вычисления этой суммы, которая является гармонической функцией той же частоты, воспользуемся методом векторных диаграмм. Каждое отдельной слагаемое изображается вектором постоянной длины a, причем каждый следующий вектор повернут относительно предыдущего на постоянный угол Δφ, если складывать эти векторы «по правилу треугольника» (Рис. 319).

Построенная таким образом векторная диаграмма вписывается в дугу окружности. Действительно, можно

построить равнобедренный треугольник C₀C₁O с вектором, изображающим колебание u₁ и углом Δφ при вершине, а затем этот треугольник n раз повернуть на тот же угол Δφ, получив таким образом полную векторную диаграмму. Вектор \(~\vec U\), изображающий результирующие колебание, соединяет начало первого вектора C₀ и конец последнего C_n. Из равнобедренного треугольника C₀OC_n с углом при вершине NΔφ определяем длину результирующего вектора, то есть амплитуду A этого колебания:

\(~A = 2 R \sin \left( \frac{N}{2} \Delta \varphi \right)\) , (5)

где R - пока не известный радиус дуги окружности, описанной вокруг векторной диаграммы. Для определения это радиуса, рассмотрим треугольник C₀C₁O и запишем для него соотношение, аналогичное (5):

\(~a = 2 R \sin \left( \frac{1}{2} \Delta \varphi \right)\) . (6)

Из выражений(5)-(6) выражаем амплитуду результирующего колебания через амплитуду волны от одного источника и разность фаз между колебаниями соседних источников:

\(~A = a \frac{\sin \left( \frac{N}{2} \Delta \varphi \right)}{\sin \left( \frac{1}{2} \Delta \varphi \right)}\) . (7)

Полученная функция очень интересна и будет встречаться в дальнейшем изложении.

Проведем анализ функции

\(~F(x) = \frac{\sin (Nx)}{\sin x}\) . (8)

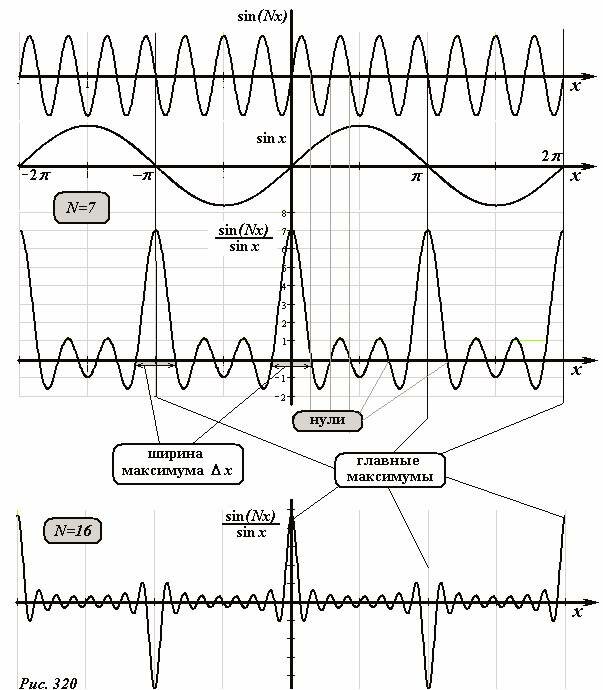
Построим схематические графики хорошо знакомых функций, стоящих в числителе и знаменателе (рис. 320). Эти функции имеют период 2π, поэтому достаточно рассмотреть эту функцию в интервале [0, 2π]; кроме того, эта функция четная.

Теперь обратим внимание, что функция, стоящая в знаменателе, обращается в нуль при x = nπ (n = 0,±1,±2...), но при этом числитель также обращается в нуль! Поэтому эту неопределенность необходимо раскрыть. Проще всего это сделать для точки x = 0. Здесь можно воспользоваться приближенной формулой sin x ≈ x, справедливой при малых x, поэтому

\(~\lim_{x \to 0} \frac{\sin (Nx)}{\sin x} = \frac{Nx}{x} = N\) . (9)

При x → π также можно найти ее предел, используя формулы приведения. Для этого обозначим x = π + ε и найдем

\(~\lim_{\varepsilon \to 0} \frac{\sin (N (\pi + \varepsilon))}{\sin (\pi + \varepsilon)} = \lim_{\varepsilon \to 0} \frac{\mp \sin (N \varepsilon)}{-\sin \varepsilon} = \pm N\) , (10)

где знак в итоговом «плюс» соответствует четным N, а «минус» нечетным. Впрочем, знак амплитуды нас не интересует (вспомните – это просто изменение фазы результирующего колебания – которая нас вообще никогда не интересовала). Важно, что рассматриваемая функция принимает максимальные по модулю значения в тех точках, где знаменатель обращается в нуль. Значения функции в этих точках x = nπ (n = 0,±1,±2...) \(|F|_{max} = N\) называются главными максимумами, именно они представляют наибольший интерес. Между главными максимумами, функция (8) имеет целый ряд побочных экстремумов (можно показать, что их число равно N − 2). Расположены они вблизи максимумов функции, стоящей в числителе, но точно не совпадают с ними. Абсолютные значения функции в этих точках не велики – около единицы. Их отношение к величине главных максимумов стремиться к нулю с ростом N. Наконец, легко указать нули анализируемой функции – они совпадают с нулями функции в числителе, кроме тех которые совпадают с нулями знаменателя. Большой практический интерес представляет ширина главного максимума Δx. В ее качестве можно взять расстояние между ближайшими к этому максимума нулями. Так первые нуль функции удовлетворяет условию

\(~N x_0 = \pi\) ,

поэтому ширина максимума равна

\(~\Delta x = 2x_0 = \frac{2 \pi}{N}\) . (11)

Вооруженные результатами математического анализа, вернемся выяснению физического смысла полученного выражения (7) для амплитуды результирующего колебания. В зависимости от суммарной разности фаз Δφ эта функция может иметь ряд резких максимумов. Так как эта разность фаз зависит от направления излучения, задаваемого углом θ (эта зависимость определяется формулой (2)), то можно ожидать, что зависимость амплитуды излучения от его направления также будет иметь резкие максимумы. Как следует из проведенного анализа, амплитуда излучения максимальна при выполнении условия

\(~\frac{\Delta \varphi}{2} = n \pi\) ,

или

\(~\Delta \varphi = 2 n \pi\) . (12)

Полученный результат очевиден – в этом случае все волны приходят в точку наблюдения в одной фазе. На векторной диаграмме все векторы колебаний отдельных волн параллельны друг другу, понятно, что модуль суммарного вектора при этом в N раз превышает амплитуду отдельной волны. Подставим выражение (2) для разности фаз колебаний и получим уравнение

\(~\varphi_0 + \frac{2 \pi}{\lambda} d \sin \theta = 2 n \pi , (n = 0, \pm 1, \pm 2 \ldots)\) , (13)

определяющее углы θ, при которых амплитуда излучения максимальна.

Отметим, что при φ₀ = 0 условие максимума приобретает уже знакомый нам вид:

\(~d \sin \theta = n \lambda , (n = 0, \pm 1, \pm 2 \ldots)\) ,

разность хода между соседними источниками должна равняться целому числу длин волн.

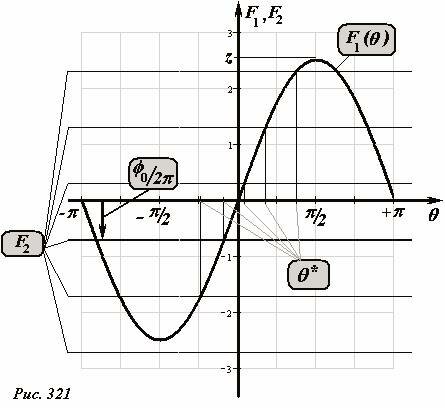
Полученное уравнение (13) является параметрическим, его решения зависят от начальной разности фаз источников. Для качественного анализа этого уравнения представим его в виде

\(~\frac{d}{\lambda} \sin \theta = n - \frac{\varphi_0}{2 \pi} , (n = 0, \pm 1, \pm 2 \ldots)\) (14)

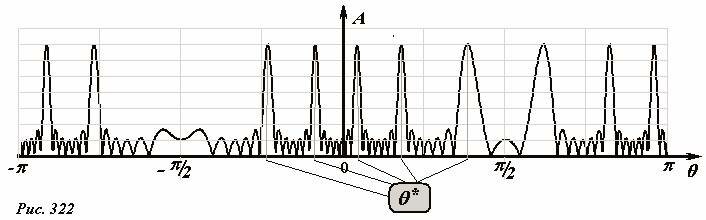
и построим графики функций \(~F_1(\theta) = \frac{d}{\lambda} \sin \theta\) - привычную синусоиду и \(~F_2(\theta) = n - \frac{\varphi_0}{2 \pi} , (n = 0, \pm 1, \pm 2 \ldots)\) - набор равноотстоящих прямых, параллельных оси абсцисс (Рис. 321). Все параметры анализируемого уравнения (14) на этом рисунке имеют явный геометрический смысл. Отношение расстояния между источниками к длине волны (обозначим этот безразмерный параметр \(~z = \frac{d}{\lambda}\)) равен «высоте» синусоиды; сдвиг фазы между колебаниями источников деленный на 2π , равен сдвигу вниз решетки параллельных линий, образованных функцией F₂. Абсциссыточек пересечения решетки F₂ с синусоидой F₁ дают значения углов θ*, которые являются корнями уравнения (14) и при которых амплитуда излучения максимальна. На рисунке отмечены только корни этого уравнения в интервале [−π, +π], потому что, именно они определяют направления излучения в одну сторону от цепочки источников. Из симметрии задачи следует, что излучение симметрично относительно оси источников. Эта симметрия отражается в корнях рассматриваемого уравнения – они симметричны относительно прямых \(~\theta = \pm \frac{\pi}{2}\). В подтверждение верности проведенного геометрического анализа на рис. 322 приведен график зависимости амплитуды излучения от угла θ, построенный как график функции (7), в которой разность фаз Δφ определяется выражением (2).

Из графика на рис. 321 можно определить, что он построен при следующих значениях параметров\[~z = \frac{d}{\lambda} = 2,5, \varphi_0 = \frac{4}{3} \pi\], эти же значения сохранены и на рис. 322 (число источников принято равным N = 7 для ровного счета) – хорошо видно, что максимумы этой сложной функции найдены верно.

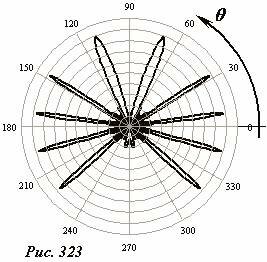
Более наглядно зависимость амплитуды излучения от направления A(θ) изображается в полярной системе координат, в которой значения функции пропорциональны расстоянию до центра вдоль радиуса, направленного под углом θ к начальному направлению (на рисунке значения углов оцифрованы в градусах). На рис. 323 представлен такой график той же зависимости, что и на рис. 322.

Согласитесь, данная система координат предпочтительнее - явно видны направления максимумов излучения. Построенный таким образом график называется индикатрисой излучения. Заметим, что чаще под индикатрисой излучения понимают зависимость интенсивности (а не амплитуды) излучения от направления. Так как энергия волны пропорциональна квадрату амплитуды, то полученные максимумы амплитуды преобразуются в еще более резкие максимумы интенсивности.

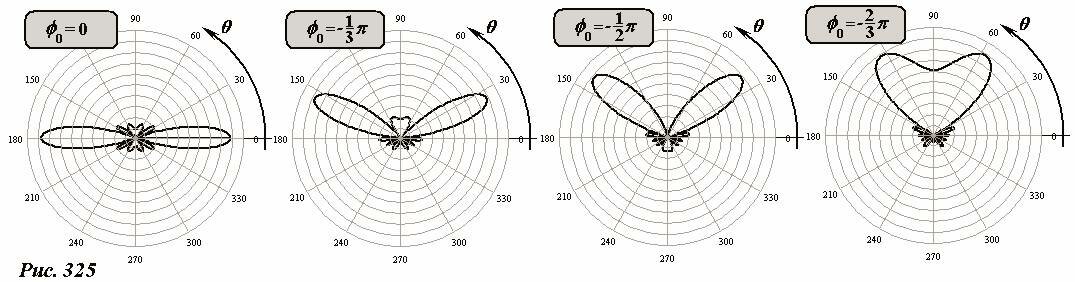
Еще раз обратимся к рисунку 321. С его помощью легко заметить, что число максимумов излучения в одну сторону от излучателя (то есть в интервале [−π, +π]) равно целой части от удвоенного значения параметра z \[~N_{max} = \left [ 2 \frac{d}{\lambda} \right]\]. Следовательно, для формирования единичного луча, необходимого для работы РЛС с подобным излучателем, расстояние между точечными источниками должно быть меньше половины длины волны излучения. На рис. 324 графически «представлено уравнение» (13) для значения \(~z = \frac{d}{\lambda} = 0,4\). В этом случае это уравнение имеет единственный корень θ * в рассматриваемом интервале, причем этот корень плавно изменяется от \(~+ \frac{\pi}{2}\) до \(~- \frac{\pi}{2}\) − при изменении сдвига фаз φ₀ от − 2πz до + 2πz. На рис. 325 изображены индикатрисы излучения такого источника (при N = 7) при различном значении сдвига фаз φ₀ колебаний точечных источников.

Как видите, действительно изменение фазы колебаний точечных источников, которое может быть осуществлено электронными методами, позволяет изменять направление максимума излучения. РЛС с таким принципом управления лучом не нуждаются в сложной, громоздкой и ненадежной механической системе управления антенной направленного излучения – система источников неподвижна, а направление излучения регулируется простым изменением фаз колебаний.

Мы рассмотрели индикатрису излучения линейной цепочки. Понятно, то эта система обладает осевой симметрией, такую же симметрию имеет и излучение – фактически построенные индикатрисы представляют сечения пространственных распределений, произвольной плоскостью, проходящей через излучатель. Иными словами – пространственной распределения максимума излучения есть конус с углом раствора θ*. Фазовые решетки современных РЛС состоят ни из одной линейной цепочки излучателей, а из прямоугольной системы таких источников (набора линейных цепочек). Задавая дополнительную разность фаз колебаний между линейными цепочками можно управлять индикатрисой излучения в перпендикулярной плоскости, то есть формировать узкий пространственный луч, направляемый в нужном направлении.

В заключение этого, итак уже затянувшегося раздела, рассмотрим вопрос об угловой ширине сформированного луча. В ходе анализа функции (8) мы установили, что ширина ее максимума определяется формулой (11). Для перехода к функции, описывающей индикатрису излучения необходимо сделать подстановку

\(~x = \frac{\Delta \varphi}{2} = \frac{1}{2} \varphi_0 + \frac{\pi}{\lambda} d \sin \theta\) . (15)

Тогда угловая ширина может быть найдена с помощью преобразования изменения аргумента x к изменению угла θ

\(~\Delta x = \Delta \left( \frac{1}{2} \varphi_0 + \frac{\pi}{\lambda} d \sin \theta \right) \approx \frac{\pi}{\lambda} d \cos \theta \cdot \Delta \theta\) . (16)

При выводе этого соотношения учтено, что начальный сдвиг φ₀ - величина постоянная, и использована приближенная формула, справедливая при малых изменениях угла \(\Delta \sin \theta \approx \cos \theta \cdot \Delta \theta\). Подставляя это выражение в формулу (11), получим равенство

\(~\Delta x = \frac{\pi}{\lambda} d \cos \theta \cdot \Delta \theta = \frac{2 \pi}{N}\) ,

из которого следует, что угловая ширина луча оценивается по формуле

\(~\Delta \theta \approx \frac{2 \lambda}{N d \cos \theta}\) , (17)

Графики на рис. 325 подтверждают полученную зависимость: при приближении угла θ к \(~\pm \frac{\pi}{2}\) угловая ширина луча растет. Отметим, что угловая ширина обратно пропорциональна общей ширине излучателя Nd, а при направлениях, близких нормали равна удвоенному отношению длины волны к ширине источника, деленному на число источников

\(~\Delta \theta \approx 2 \frac{\lambda}{N d}\) . (18)

Обратите внимание на этот результат, с подобными оценками углового распределения излучения мы встретимся не раз.

Мы рассмотрели индикатрису излучения линейной цепочки. Понятно, то эта система обладает осевой симметрией, такую же симметрию имеет и излучение – фактически построенные индикатрисы представляют сечения пространственных распределений, произвольной плоскостью, проходящей через излучатель. Иными словами – пространственной распределения максимума излучения есть конус с углом раствора θ*. Фазовые решетки современных РЛС состоят ни из одной линейной цепочки излучателей, а из прямоугольной системы таких источников (набора линейных цепочек). Задавая дополнительную разность фаз колебаний между линейными цепочками можно управлять индикатрисой излучения в перпендикулярной плоскости, то есть формировать узкий пространственный луч, направляемый в нужном направлении.

Задание для самостоятельной работы.

1. Найдите, по какому закону должна меняться со временем разность фаз между источниками φ₀(t), чтобы направленный луч вращался в пространстве с постоянной угловой скоростью.

Примечания

Следующая страница