Слободянюк А.И. Физика 10/12.10
§12. Постоянное магнитное поле
12.10 Электрические и магнитные силы – что больше?
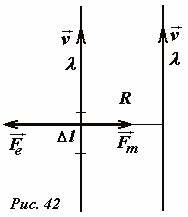
Проведем численное сравнение электрических и магнитных сил в простом примере. Две длинные параллельные равномерно заряженные с линейной плотностью заряда λ нити движутся с постоянными и одинаковыми скоростями, причем векторы скоростей \(~\vec \upsilon\) направлены вдоль нитей (Рис. 42). Расстояние между нитями обозначим R. Движущиеся заряженные нити создают постоянный электрический ток, силу которого можно найти по определению, как заряд, протекающий через поперечное сечение в единицу времени:
Силу, действующую на участок одной нити длиной Δl со стороны магнитного поля, рассчитаем по формуле для взаимодействия параллельных токов
Со стороны электрического поля на этот же участок действует сила
где E - напряженность электрического поля, создаваемого другой нитью.
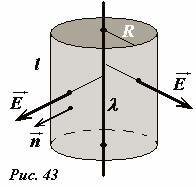
Для расчета этого поля воспользуемся теоремой Гаусса: поток вектора напряженности электрического поля через любую замкнутую поверхность равен заряду, находящемуся внутри этой поверхности, деленному на электрическую постоянную. В качестве замкнутой поверхности выберем цилиндр длиной l радиуса R, соосный с нитью (рис. 43). На боковой поверхности вектор напряженности электрического поля постоянен по модулю и направлен нормально к поверхности (это следует из цилиндрической симметрии системы), поэтому поток через эту поверхность равен произведению модуля вектора напряженности на площадь боковой поверхности \(~\Phi_E = E \cdot 2 \pi Rl\) . Поток через основания цилиндра равен нулю, так в любой точке оснований векторы напряженности и нормали к поверхности перпендикулярны. Из теоремы Гаусса (\(~\Phi_E = \frac{q}{\varepsilon_0}\)) следует равенство \(~E \cdot 2 \pi Rl = \frac{\lambda l}{\varepsilon_0}\) , где λl - заряд, находящийся внутри цилиндра. Итак, искомая напряженность поля равна [1]
Следовательно, сила, действующая на выделенный участок со стороны электрического поля, рассчитывается по формуле (очень похожей на формулу (2))
Отношение этих сил магнитного и электрического взаимодействия равно
Мы получили удивительно простую формулу. Рассчитанная величина должна быть безразмерной, поэтому величина \(~c = \frac{1}{\sqrt{\varepsilon_0 \mu_0}}\) должна иметь размерность скорости! (Проверьте самостоятельно, что это действительно так!) Вычислим ее:
Полученное значение совпадает с экспериментально измеренной скоростью света в вакууме. Это совпадение не является случайным. Дж. К. Максвелл на основании своих уравнений показал, что электромагнитное поле может существовать в идее волн, скорость которых определяется формулой [2] (5) . На основании этого результата он сделал пророческий вывод – свет является электромагнитной волной, который в последствии был надежно подтвержден экспериментально.
Теперь формулу (4) можно записать в виде
из которого наглядно видно, что при небольших (по сравнению с громадной скоростью света) скоростях магнитная сила является крайне незначительной добавкой. В начале наших рассуждений о магнитном поле, мы рассматривали вопрос об относительности движения и ее влиянии на электрические и магнитные явления. Теперь мы можем дать численную оценку «магнитной добавки» к электрическому взаимодействию. Если рассмотренные нити движутся со скоростью звука υ ≈ 3,3·102 м/с (то есть находятся на очень скоростном самолете), то отношение магнитной силы к электрической равно \(~\frac{F_m}{F_e} = \frac{\upsilon^2}{c^2} \approx 10^{-12}\) , то есть пренебрежимо мало, и не может быть обнаружено экспериментально. Итак, для зарядов, движущихся с «обычными» скоростями с высокой степенью можно пользоваться формулами электростатики.
Магнитные взаимодействия проявляются тогда, когда в системе отсутствую электрические взаимодействия. Так проводники, по которым текут электрические токи, являются электрически нейтральными, поэтому для них можно наблюдать магнитные эффекты «в чистом виде», а не на фоне мощных электрических явлений.
Примечания
- ↑ Строго говоря, поле электрическое поле движущих зарядов отличается от поля неподвижных зарядов, однако при малых скоростях движения эти отличия пренебрежимо малы.
- ↑ Будем честны – Дж. К. Максвелл пользовался другой системой единиц измерения, поэтому он не мог получить в точности именно эту формулу, он получил эквивалентное соотношение в другой системе единиц, важно, что вычисленная им скорость электромагнитных волн совпала со скоростью света!
Смотреть HD
видео онлайн
бесплатно 2022 года