Слободянюк А.И. Физика 10/12.11
§12. Постоянное магнитное поле
12.11 Магнитный поток, теорема о магнитном потоке.
Ранее мы убедились насколько полезно и удобно понятие потока векторного поля. Не является исключением и описание магнитного поля – для него также определяется поток, и формулируется теорема об этом потоке.
Поток вектора магнитной индукции (который также называется магнитным потоком) определяется традиционно [1]. Пусть в некоторой малой области пространства существует магнитное поле, которое можно считать однородным, то есть в этой области вектор магнитной индукции постоянен, как по величине, так и по направлению.
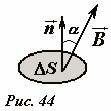
Выделим малую площадку площадью ΔS, ориентация которой задается единичным вектором нормали \(~\vec n\) (Рис. 44). Магнитный поток через эту площадку ΔФm определяется как произведение площади площадки на нормальную составляющую вектора индукции магнитного поля
где \(~(\vec B \cdot \vec n) = B \cos \alpha\) - скалярное произведение векторов \(~\vec B\) и \(~\vec n\); Bn - нормальная к площадке компонента вектора магнитной индукции.
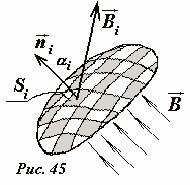
В произвольном магнитном поле магнитный поток через произвольную поверхность, определяется следующим образом (Рис. 45):
- - поверхность разбивается на малые площадки ΔSi (которые можно считать плоскими);
- - определяется вектор индукции \(~\vec B_i\) на этой площадке (который в пределах площадки можно считать постоянным);
- - вычисляется сумма потоков через все площадки, на которые разбита поверхность
Эта сумма называется потоком вектора индукции магнитного поля через заданную поверхность (или магнитным потоком).
Обратите внимание, что при вычислении потока суммирование проводится по точкам наблюдения поля, а не по источникам, как при использовании принципа суперпозиции. Поэтому магнитный поток является интегральной характеристикой поля, описывающей его усредненные свойства на всей рассматриваемой поверхности.
Трудно найти физический смысл магнитного потока, как и для иных полей это полезная вспомогательная физическая величина. Но в отличие от других потоков, магнитный поток настолько часто встречается в приложениях, что в системе СИ удостоился «персональной» единицы измерения - Вебер: 1 Вебер – магнитный поток однородного магнитного поля индукции 1 Тл через площадку площадью 1 м2 ориентированную перпендикулярно вектору магнитной индукции.
Теперь докажем простую, но чрезвычайно важную теорему о магнитном потоке через замкнутую поверхность.
Ранее мы установили, что силовые любого магнитного поля являются замкнутыми, уже из этого следует, что магнитный поток, через любую замкнутую поверхность равен нулю.
Тем не менее, приведем более формальное доказательство этой теоремы.
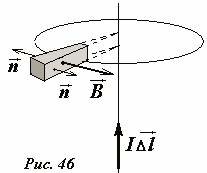
Прежде всего, отметим, что для магнитного потока справедлив принцип суперпозиции: если магнитное поле создано несколькими источниками, то для любой поверхности поток поля, созданного системой элементов тока, равен сумме потоков полей, созданных каждым элементом тока в отдельности. Это утверждение следует непосредственно из принципа суперпозиции для вектора индукции и прямо пропорциональной связью между магнитным потоком и вектором магнитной индукции. Следовательно достаточно доказать теорему для поля, созданного элементом тока, индукция которого определяется по закону Био-Саварра-Лапласа. Здесь для нас важна структура поля, обладающего осевой круговой симметрией, значение модуля вектора индукции несущественно. Выберем в качестве замкнутой поверхности поверхность бруска, вырезанного, как показано на рис. 46. Магнитный поток отличен от нуля только через его две боковые грани, но эти потоки имеют противоположные знаки. Вспомним, что для замкнутой поверхности выбираю внешнюю нормаль, поэтому на одной из указанных граней (передней) поток положительный, а на задней отрицательный. Причем модули этих потоков равны, так как распределение вектора индукции поля на этих гранях одинаково. Данный результат не зависит от положения рассмотренного бруска. Произвольное тело можно разбить на бесконечно малые части, каждая из которых подобна рассмотренному бруску.
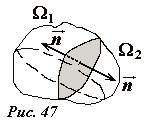
Наконец, сформулируем еще одно важное свойство потока любого векторного поля. Пусть произвольная замкнутая поверхность ограничивает некоторое тело (Рис. 47). Разобьем это тело на две части, ограниченные частями исходной поверхности Ω1 и Ω2, и замкнем их общей границей раздела тела. Сумма потоков через эти две замкнутые поверхности равна потоку через исходную поверхность! Действительно сумма потоков через границу (один раз для одного тела, другой раз для другого) равна нулю, так как в каждом случае надо брать разные, противоположные нормали (каждый раз внешнюю). Аналогично можно доказать утверждение для произвольного разбиения тела: если тело разбито на произвольное число частей, то поток через поверхность тела равен сумме потоков через поверхности всех частей разбиения тела. Это утверждение очевидно для потока жидкости.
Фактически мы доказали, что если поток векторного поля равен нулю через некоторую поверхность ограничивающее малый объем, то этот поток равен нулю через любую замкнутую поверхность.
Итак, для любого магнитного поля справедлива теорема о магнитном потоке: магнитный поток через любую замкнутую поверхность равен нулю Фm = 0.
Ранее мы рассматривали теоремы о потоке для поля скоростей жидкости и электростатического поля. В этих случаях поток через замкнутую поверхность полностью определялся точечными источниками поля (истоками и стоками жидкости, точечными зарядами). В общем случае наличие ненулевого потока через замкнутую поверхность свидетельствует о наличии точечных источников поля. Следовательно, физическим содержанием теоремы о магнитном потоке является утверждение об отсутствии магнитных зарядов.
Если вы хорошо разобрались в данном вопросе и сумеете объяснить и отстоять свою точку зрения, то можете формулировать теорему о магнитном потоке и так: «Еще никто не нашел монополя Дирака».
Следует особо подчеркнуть, что, говоря об отсутствии источников поля, мы имеем виду именно точечных источников, подобных электрическим зарядам. Если провести аналогию с полем движущейся жидкости, электрические заряды подобны точкам, из которых вытекает (или втекает) жидкость, увеличивая или уменьшая ее количество. Возникновение магнитного поля, благодаря движению электрических зарядов подобно движению тела в жидкости, которое приводит к появлению вихрей, не изменяющих общего количества жидкости.
Векторные поля, для которых поток через любую замкнутую поверхность равен нулю получили красивое, экзотическое название – соленоидальные. Соленоидом называется проволочная катушка, по которой можно пропускать электрический ток. Такая катушка может создавать сильные магнитные поля, поэтому термин соленоидальный означает «подобный полю соленоида», хотя можно было назвать такие поля попроще – «магнитоподобные». Наконец такие поля еще называют вихревыми, подобно полю скоростей жидкости, образующей в своем движении всевозможные турбулентные завихрения.
Теорема о магнитном потоке имеет большое значение, она часто используется при доказательстве различных свойств магнитных взаимодействий, с ней мы будем встречаться неоднократно. Так, например, теорема о магнитном потоке доказывает, что вектор индукции магнитного поля, создаваемого элементом, не может иметь радиальной составляющей (Рис. 23.а), иначе поток через цилиндрическую поверхность коаксиальную с элементом тока был бы отличен от нуля.
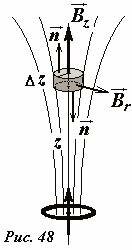
Теперь проиллюстрируем применение теоремы о магнитном потоке для расчета индукции магнитного поля. Пусть магнитное поле создается кольцом с током, которое характеризуется магнитным моментом pm. Рассмотрим поле вблизи оси кольца на расстоянии z от центра, значительно большем радиуса кольца (Рис. 48). Ранее мы получили формулу для индукции магнитного поля на оси для больших расстояний от центра кольца
Мы не допустим большой ошибки, если будем считать, что такое же значение имеет вертикальная (пусть ось кольца вертикальна) компонента поля в пределах небольшого кольца радиуса r, плоскость которого перпендикулярна оси кольца. Так как вертикальная компонента поля изменяется с изменением расстояния, то неизбежно должны присутствовать радиальные компоненты поля, иначе не будет выполняться теорема о магнитном потоке! Оказывается этой теоремы и формулы (3) достаточно, чтобы найти эту радиальную компоненту. Выделим тонкий цилиндр толщиной Δz и радиуса r, нижнее основание которого находится на расстоянии z от центра кольца, соосный с кольцом и применим теорему о магнитном потоке к поверхности этого цилиндра. Магнитный поток через нижнее основание равен (учтите, что вектора индукции и нормали здесь противоположны)
где Bz(z) - значение вертикальной компоненты вектора индукции на высоте z; поток через верхнее основание равен
где Bz(z + Δz) - значение вертикальной компоненты вектора индукции на высоте z + Δz;
поток через боковую поверхность (из осевой симметрии следует, что модуль радиальной составляющей вектора индукции Br на этой поверхности постоянен):
По доказанной теореме сумма этих потоков равна нулю, поэтому справедливо уравнение
из которого определим искомую величину
Осталось использовать формулу (3) для вертикальной составляющей поля и провести необходимые вычисления [2]
Действительно, убывание вертикальной компоненты поля приводит к появлению горизонтальных компонент: уменьшение вытекания через основания приводит к «течи» через боковую поверхность.
Таким образом, мы доказали «криминальную теорему»: если через один конец трубы вытекает меньше, чем вливают в нее с другого конца, то где-то воруют через боковую поверхность.
Примечания
- ↑ Достаточно взять текст с определением потока вектора напряженности электрического поля и изменить обозначения (что здесь и сделано).
- ↑ Самые грамотные могут увидеть в последней дроби производную функции (3) и элементарно ее вычислить, нам же придется очередной раз воспользоваться приближенной формулой \(~(1 + x)^\beta \approx 1 + \beta x\)