КС. Относительность движения

Относительность движения

Слова «тело движется» не имеют определенного смысла, так как нужно сказать, по отношению к каким телам или относительно какой системы отсчета это движение рассматривается. Приведем несколько примеров.

Пассажиры движущегося поезда неподвижны относительно стен вагона. И те же пассажиры движутся в системе отсчета, связанной с Землей. Поднимается лифт. Стоящий на его полу чемодан покоится относительно стен лифта и человека, находящегося в лифте. Но он движется относительно Земли и дома.

Эти примеры доказывают относительность движения и, в частности, относительность понятия скорости. Скорость одного и того же тела различна в разных системах отсчета.

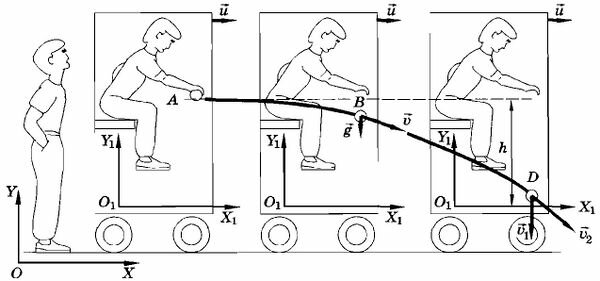
Представьте себе пассажира в движущемся равномерно относительно поверхности Земли вагоне, выпускающего из рук мяч. Он видит, как мяч падает относительно вагона вертикально вниз с ускорением g. Свяжем с вагоном систему координат X₁О₁Y₁ (рис. 1). В этой системе координат за время падения мяч пройдет путь AD = h, и пассажир отметит, что мяч упал вертикально вниз и в момент удара о пол его скорость υ₁.

Рис. 1

Ну а что увидит наблюдатель, стоящий на неподвижной платформе, с которой связана система координат XOY? Он заметит (представим себе, что стены вагона прозрачны), что траекторией мяча является парабола AD, и мяч упал на пол со скоростью υ₂, направленной под углом к горизонту (см. рис. 1).

Итак, мы отмечаем, что наблюдатели в системах координат X₁О₁Y₁ и XOY обнаруживают различные по форме траектории, скорости и пройденные пути при движении одного тела — мяча.

Надо отчетливо представлять себе, что все кинематические понятия: траектория, координаты, путь, перемещение, скорость имеют определенную форму или численные значения в одной выбранной системе отсчета. При переходе от одной системы отсчета к другой указанные величины могут измениться. В этом и состоит относительность движения, и в этом смысле механическое движение всегда относительно.

Связь координат точки в системах отсчета, движущихся друг относительно друга, описывается преобразованиями Галилея. Преобразования всех других кинематических величин являются их следствиями.

Пример. Человек идет по плоту, плывущему по реке. Известны и скорость человека относительно плота, и скорость плота относительно берега.

В примере идет речь о скорости человека относительно плота и скорости плота относительно берега. Поэтому одну систему отсчета K свяжем с берегом — это неподвижная система отсчета, вторую К₁ свяжем с плотом — это подвижная система отсчета. Введем обозначения скоростей:

• 1 вариант (скорость относительно систем)

υ — скорость тела относительно неподвижной системы отсчета К (скорость человека относительно Земли);

υ₁ — скорость этого же тела относительно подвижной системы отсчета K₁ (скорость человека относительно плота);

u — скорость подвижной системы К₁ относительно неподвижной системы К (скорость плота относительно Земли). Тогда

$\vec{\upsilon }=\vec{u}+\vec{\upsilon }_{1} .\; \; \; (1)$

• ”2 вариант

υ_тон — скорость тела относительно неподвижной системы отсчета К (скорость человека относительно Земли);

υ_топ — скорость этого же тела относительно подвижной системы отсчета K₁ (скорость человека относительно плота);

υ_с — скорость подвижной системы К₁ относительно неподвижной системы К (скорость плота относительно Земли). Тогда

$\vec{\upsilon }_{тон} =\vec{\upsilon }_{c} +\vec{\upsilon }_{топ} .\; \; \; (2)$

• 3 вариант

υ_а (абсолютная скорость) — скорость тела относительно неподвижной системы отсчета К (скорость человека относительно Земли);

υ_от (относительная скорость) — скорость этого же тела относительно подвижной системы отсчета K₁ (скорость человека относительно плота);

υ_п (переносная скорость) — скорость подвижной системы К₁ относительно неподвижной системы К (скорость плота относительно Земли). Тогда

$\vec{\upsilon }_{a} =\vec{\upsilon }_{от} +\vec{\upsilon }_{n} .\; \; \; (3)$

• 4 вариант

υ₁ или υ_чел — скорость первого тела относительно неподвижной системы отсчета К (скорость человека относительно Земли);

υ₂ или υ_пл — скорость второго тела относительно неподвижной системы отсчета К (скорость плота относительно Земли);

υ_1/2 или υ_чел/пл — скорость первого тела относительно второго (скорость человека относительно плота);

υ_2/1 или υ_пл/чел — скорость второго тела относительно первого (скорость плота относительно человека). Тогда

$\left|\begin{array}{c} {\vec{\upsilon }_{1} =\vec{\upsilon }_{2} +\vec{\upsilon }_{1/2} ,\; \; \, \, \vec{\upsilon }_{2} =\vec{\upsilon }_{1} +\vec{\upsilon }_{2/1} ;} \\ {} \\ {\vec{\upsilon }_{чел} =\vec{\upsilon }_{пл} +\vec{\upsilon }_{чел/пл} ,\; \; \, \, \vec{\upsilon }_{пл} =\vec{\upsilon }_{чел} +\vec{\upsilon }_{пл/чел} .} \end{array}\right. \; \; \; (4)$

Формулы (1-4) можно записать и для перемещений Δr, и для ускорений a:

$\begin{array}{c} {\Delta \vec{r}_{тон} =\Delta \vec{r}_{c} +\Delta \vec{r}_{топ} ,\; \; \; \Delta \vec{r}_{a} =\Delta \vec{r}_{от} +\Delta \vec{п}_{?} ,} \\ {} \\ {\Delta \vec{r}_{1} =\Delta \vec{r}_{2} +\Delta \vec{r}_{1/2} ,\; \; \, \, \Delta \vec{r}_{2} =\Delta \vec{r}_{1} +\Delta \vec{r}_{2/1} ;} \\ {} \\ {\vec{a}_{тон} =\vec{a}_{c} +\vec{a}_{топ} ,\; \; \; \vec{a}_{a} =\vec{a}_{от} +\vec{a}_{п} ,} \\ {} \\ {\vec{a}_{1} =\vec{a}_{2} +\vec{a}_{1/2} ,\; \; \, \, \vec{a}_{2} =\vec{a}_{1} +\vec{a}_{2/1} .} \end{array}$

План решения задач на относительность движения

1. Сделайте чертеж: тела изобразите в виде прямоугольников, над ними укажите направления скоростей и перемещений (если они нужны). Выберите направления осей координат.

2. Исходя из условия задачи или по ходу решения, определитесь с выбором подвижной системы отсчета (СО) и с обозначениями скоростей и перемещений.

• Всегда начинайте с выбора подвижной СО. Если в задаче нет специальных оговорок, относительно какой СО заданы (или нужно найти) скорости и перемещения, то не принципиально, какую систему принять за подвижную СО. Удачный выбор подвижной системы существенно упрощает решение задачи.
• Обратите внимание на то, чтобы одна и та же скорость (перемещение) обозначалась одинаково в условии, решении и на рисунке.

3. Запишите закон сложения скоростей и (или) перемещений в векторном виде:

$\vec{\upsilon }_{тон} =\vec{\upsilon }_{c} +\vec{\upsilon }_{топ} ,\; \; \, \, \Delta \vec{r}_{тон} =\Delta \vec{r}_{c} +\Delta \vec{r}_{топ} .$

• Не забывайте и про другие варианты записи закона сложения:

$\begin{array}{c} {\vec{\upsilon }_{a} =\vec{\upsilon }_{от} +\vec{\upsilon }_{п} ,\; \; \; \Delta \vec{r}_{a} =\Delta \vec{r}_{от} +\Delta \vec{r}_{п} ,} \\ {} \\ {\vec{\upsilon }_{1} =\vec{\upsilon }_{2} +\vec{\upsilon }_{1/2} ,\; \; \, \, \Delta \vec{r}_{1} =\Delta \vec{r}_{2} +\Delta \vec{r}_{1/2} .} \end{array}$

4. Запишите проекции закона сложения на оси 0Х и 0Y (и другие оси)

0Х: υ_{тон x} = υ_{с x} + υ_{топ x},   Δr_{тон x} = Δr_{с x} + Δr_{топ x},   (5-6)

0Y: υ_{тон y} = υ_{с y} + υ_{топ y},   Δr_{тон y} = Δr_{с y} + Δr_{топ y},   (7-8)

• Другие варианты:

0Х: υ_{a x} = υ_{от x} + υ_{п x},   Δr_{а x} = Δr_{от x} + Δr_{п x},

υ_1x = υ_2x + υ_1/2x,   Δr_1x = Δr_2x + Δr_1/2x,

0Y: υ_{a y} = υ_{от y} + υ_{п y},   Δr_{а y} = Δr_{от y} + Δr_{п y},

υ_1y = υ_2y + υ_1/2y,   Δr_1y = Δr_2y + Δr_1/2y.

5. Найдите значения проекций каждой величины:

υ_{тон x} = …, υ_{с x} = …, υ_{топ x} = …,

Δr_{тон x} = …, Δr_{с x} = …, Δr_{топ x} = …,

υ_{тон y} = …, υ_{с y} = …, υ_{топ y} = …,

Δr_{тон y} = …, Δr_{с y} = …, Δr_{топ y} = …

• Аналогично для других вариантов.

6. Подставьте полученные значения в уравнения (5) - (8).

7. Решите полученную систему уравнений.

• Примечание. По мере наработки навыка решения таких задач, пункты 4 и 5 можно будет делать в уме, без записи в тетрадь.

Дополнения

1. Если заданы скорости тел относительно тел, которые сейчас неподвижны, но могут двигаться (например, скорость тела в озере (нет течения) или в безветренную погоду), то такие скорости считают заданными относительно подвижной системы (относительно воды или ветра). Это собственные скорости тел, относительно неподвижной системы они могут меняться. Например, собственная скорость человека 5 км/ч. Но если человек идет против ветра, его скорость относительно земли станет меньше; если ветер дует в спину, скорость человека будет больше. Но относительно воздуха (ветра) его скорость остается равной 5 км/ч.
2. В задачах обычно фразу «скорость тела относительно земли» (или относительно любого другого неподвижного тела), по умолчанию, заменяют на «скорость тела». Если скорость тела задана не относительно земли, то это должно быть указано в условии задачи. Например, 1) скорость самолета 700 км/ч, 2) скорость самолета в безветренную погоду 750 км/ч. В примере один, скорость 700 км/ч задана относительно земли, во втором — скорость 750 км/ч задана относительно воздуха (см. дополнение 1).
3. В формулах, в которые входят величины с индексами, должен выполняться принцип соответствия, т.е. индексы соответствующих величин должны совпадать. Например, $t=\dfrac{\Delta r_{тон x} }{\upsilon _{тон x}} =\dfrac{\Delta r_{c x}}{\upsilon _{c x}} =\dfrac{\Delta r_{топ x}}{\upsilon _{топ x}}$.
4. Перемещение при прямолинейном движении направлено в ту же сторону, что и скорость, поэтому знаки проекций перемещения и скорости относительно одной и той же системы отсчета совпадают.