А. Сложение колебаний
Принцип суперпозиции. Сложение колебаний
Часто тело участвует в двух или нескольких колебаниях. Например, груз, подвешенный на пружине к потолку рессорного вагона, колеблется относительно точки подвеса, которая в свою очередь совершает колебания вместе с вагоном на его рессорах. Таким образом, груз будет совершать движение, складывающееся из двух колебаний. В таких случаях необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. По принципу суперпозиции эти колебания рассматриваются как независимые, и результирующее смещение находится в каждый момент времени как векторная сумма смещений отдельных колебаний. В случае сложения колебаний, направленных по одной прямой, результирующее смещение равно алгебраической сумме смещений отдельных колебаний.
При сложении колебаний можно пользоваться аналитическим, графическим методами и методом векторных диаграмм.
Сложим гармонические колебания одного направления и одинаковой частоты:
1. Аналитический метод. Результирующее смещение
Покажем, что результирующее колебание также является гармоническим колебанием той же частоты, т.е. что
где А — амплитуда результирующего колебания; \(\varphi\) — его начальная фаза. Тогда
Используя формулу косинуса суммы двух углов, получим
Это уравнение будет тождеством относительно t, если коэффициенты при \(~\cos \omega t\) и \(~\sin \omega t\) в его левой части равны соответствующим коэффициентам в правой части в любой момент времени:
Решив эту систему уравнений, получим
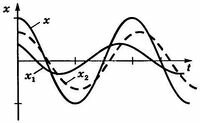
2. Графический метод. Сложение сводится к суммированию ординат в каждый момент времени (чем больше точек, тем точнее) — рисунок 13.6.
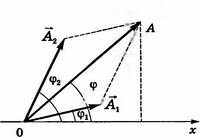
3. Метод векторных диаграмм. Построим векторные диаграммы этих колебаний (рис. 13.7). Так как векторы \(\vec A_1\) и \(\vec A_2\) вращаются с одинаковой угловой скоростью, то угол между ними, а значит, и разность фаз \((\varphi_2 - \varphi_1)\) составляющих колебаний, остаются постоянными. Результирующее смещение \(~x = x_1 + x_2\), где х1 + х2 — сумма проекций векторов \(\vec A_1\) и \(\vec A_2\) на ось Ох. Из математики известно, что сумма проекций векторов равна проекции вектора суммы, т.е. \(~A_{1x} + A_{2x}=A_x,\) где \(A = \vec A_1 + \vec A_2.\) Следовательно, амплитуда результирующего колебания равна модулю вектора \(\vec A\). Из рисунка 13.7 видно, что по теореме косинусов
Угол наклона \(\varphi\) вектора к оси Ох равен начальной фазе результирующего колебания. Из рисунка 13.7 видно, что Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз \(\varphi_2-\varphi_1\) При сложении гармонических колебаний одного направления, но разных частот, результирующее колебание не является гармоническим. Еще более сложными оказываются результирующие колебания, полученные при сложении колебаний, происходящих в разных направлениях.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 371-373.
Смотреть HD
видео онлайн
бесплатно 2022 года