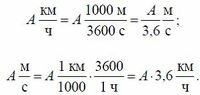КС. Понятия кинематики
Вводный курс по кинематике
Траектория — это линия, вдоль которой движется тело.
Путь — это длина участка траектории, пройденного точкой за данный промежуток времени.
- Обозначается буквой s, измеряется в метрах (м).
Перемещение — вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
- Обозначается — $\Delta \vec{r}$, измеряется в метрах (м).
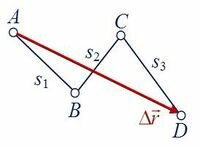
Например, пусть тело движется из точки A в точку D по ломанной линии ABCD (рис. 1), тогда путь $s=s_{1} +s_{2} +s_{3},$ перемещение $\Delta \vec{r}=\overrightarrow{AD}$.
Скорость равномерного прямолинейного движения — постоянная векторная величина, равная отношению перемещения тела $\Delta \vec{r}$ за некоторый промежуток времени t к значению этого промежутка, т.е.
- Обозначается — $\vec{\upsilon }$, измеряется в метрах в секунду (м/с).
- Для перевода км/ч в м/с и наоборот:
Средняя скорость пути $\langle \upsilon \rangle $ — это величина, равная отношению всего пройденного пути s к тому промежутку времени t, за который этот путь проделан, т.е.
- Если весь путь можно разбить на отдельные участки пути s1, s2 , s3, …, а t1, t2, t3, … — это промежутки времени, за которые тело проходит эти отдельные участки, то
Средняя скорость перемещения $\langle \vec{\upsilon }\rangle $ — это векторная величина, равная отношению вектора перемещения $\Delta \vec{r}$ к тому промежутку времени t, за который это перемещение произошло, т.е.
- Если все перемещение можно разбить на отдельные участки перемещений $\Delta \vec{r}_{1} ,\; \Delta \vec{r}_{2} ,\; \Delta \vec{r}_{3} ,\; \ldots $ а t1, t2, t3, … — это промежутки времени, за которые тело проходит эти отдельные участки, то
Смотреть HD
видео онлайн
бесплатно 2022 года