Kvant. Волны на пляже
Стасенко А.Л. Волны на пляже, Солнце в небе и многое другое //Квант. — 1995. — № 3. — С. 37-38.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Гляди в оба!
Народная мудрость
Рыба анаблепа живет на поверхности воды. Ее глаз разделен на два сектора: верхний видит в воздухе,
нижний — в воде. Одним взглядом анаблепа замечает сразу и птиц в небе, и рыб в водоеме.
Из научной книги
Конечно, почти всякая рыба имеет некоторое отношение к волнам и пляжам. Но не в этом дело. А дело в том, что хотелось бы понять, почему на пляжах волны всегда бьются о берег параллельно ему, откуда бы ни дул ветер и как бы волны ни были направлены в открытом море. Иначе говоря, почему линии, перпендикулярные гребням волн, т.е. их лучи, искривляются так, что к берегу они подходят под прямым углом.
Оказывается, это имеет прямое отношение к преломлению луча света при переходе из одной среды в другую, скажем из воздуха в воду. Тут все понятно: в воздухе свет распространяется со скоростью υ1, в воде — с меньшей скоростью υ2 (υ2 < υ1) их отношение называется показателем (коэффициентом) преломления воды относительно воздуха
а из закона преломления
описанного в школьном учебнике (правда в несколько ином виде), следует, что при переходе в оптически более плотную
среду (при n > 1) преломленный луч пойдет ближе к нормали, чем падающий, т.е. α2 < α1.
Как можно убедиться, вывод этого закона не зависит от физической природы волны (и это нам пригодится в дальнейшем).
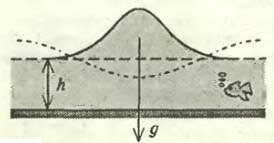
Найдем прежде всего скорость распространения волн на пляже. Отчего она может зависеть? Если мы создадим «горб» на поверхности спокойной воды — моря, озера или лужи — глубиной h (рис.1) и предоставим его самому себе, то под действием силы тяготения (пропорциональной ускорению свободного падения g) он начнет проваливаться вниз, а вследствие инерции проскочит положение, соответствующее спокойной поверхности, рядом возникнут другие «горбы», и начнет распространяться волна.
Перечислим величины (и их размерности) , от которых, по нашему мнению, может зависеть искомая скорость движения волны υ (м/с) : h (м), g (м/с2).
Из соображений размерностей сразу видно, что их можно связать формулой (проверьте)
Таким образом, чем мельче водоем, тем с меньшей скоростью распространяется волна (разумеется, это справедливо только для мелкой воды, когда скорость не зависит от длины волны). Значит, с приближением к берегу и уменьшением глубины водоема волны движутся все медленнее. По аналогии с оптикой, можно сказать, что они переходят во все более оптически плотную среду. (Кстати, и в стакане с водой тоже можно создать среду с показателем преломления, плавно растущим по направлению к его дну, если сделать очень концентрированный раствор соли, а затем осторожно, избегая перемешивания слоев, добавлять к нему все менее соленые слои и, наконец, чистую воду (попробуйте!). Тогда подводная часть ложки будет выглядеть не преломленной, а плавно изогнутой.)
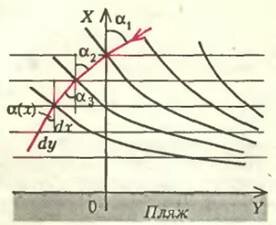
Разобьем мысленно поверхность моря на полосы шириной dx, параллельные берегу (рис.2). В каждом слое будет своя глубина h, своя скорость распространения волны, свой показатель преломления, обратно пропорциональный этой скорости, и свой угол по отношению к оси X, перпендикулярной берегу. Тогда закон преломления (1) для всех этих слоев можно записать в виде
Уже отсюда видно, что если глубина стремится к нулю, то угол между лучом и нормалью тоже стремится к нулю. Это и объясняет, почему волны на пляжах «плюхают» прямо в берег. Но можно пойти и дальше — найти само уравнение луча.
Исходя из рисунка 3, запишем
Воспользуемся выражением (3), и мы получим связь между наклоном волны по отношению к нормали на любом расстоянии х от берега с его значением α1, на каком-то фиксированном расстоянии x1:
А теперь осталось только «назначить» зависимость глубины от расстояния до берега h(х) — и интегрируйте себе на здоровье! Ну например, возьмем квадратичный закон \(~h = h_1 \left(\frac{x}{x_1} \right)^2\) . Тогда получим
Можно спросить у математиков, как вычислить этот интеграл. А можно и попробовать самим. Сделаем такую замену переменной:
и продифференцируем:
Подставляя все это в подынтегральное выражение, получим
Это уже и есть искомая зависимость — уравнение луча у(x). Но как бы назвать эту кривую? Перенесем первое слагаемое в правой части влево, возведем обе части в квадрат, а затем оставим справа только единицу:
Даведь это уравнение окружности! (Разумеется, при другой зависимости глубины от расстояния получится иное уравнение луча.) Однако пойдем дальше. Уравнение (1) объясняет множество других явлений природы.
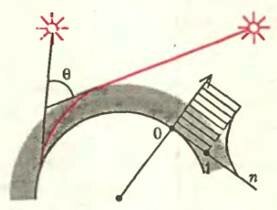
Например, атмосферную рефракцию солнечных лучей (рис.3). Поскольку плотность атмосферы растет по направлению к поверхности Земли, коэффициент преломления воздуха падает с высотой, и лучи Солнца изгибаются так, что наблюдатель на Земле видит его еще некоторое время после геометрического захода и перед восходом. В результате световой день удлиняется на несколько минут, что очень полезно (для колхозных полей, например). Благодаря этому же явлению в высоких широтах полярная «ночь» короче полярного «дня», что тоже очень хорошо.
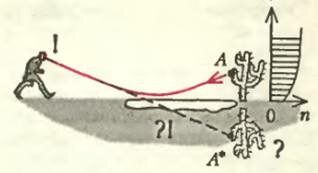
Этим же уравнением можно объяснить миражи в пустыне. Когда раскаленный песок подогревает прилежащий слой воздуха, реализуется ситуация, при которой показатель преломления верхнего слоя больше, чем нижнего. В результате лучи, идущие, например, из точки А (рис.4), изгибаются кверху, так что усталый путник принимает точку А* за отражение в столь желанном озере, которого, увы, нет.
Кстати, о рыбе. Пусть даже не об упомянутой анаблепе, а о самой простой. Показатель преломления ее среды обитания — воды — заметно больше единицы (\(~n \approx \frac 43\)). Но для того чтобы фокусировать лучи, коэффициент преломления ее глаз должен быть еще больше. Что же, природа должна создавать рыбий глаз из кронгласа или флинта? Это вопрос нетривиальный, и как он решен Природой — об этом можно поговорить или почитать отдельно. Здесь интересно вспомнить, что знаменитый физик Максвелл придумал такой инструмент (он назвал его «рыбьим глазом»), который представляет собою неограниченную среду с показателем преломления, зависящим только от расстояния (r) до фиксированной точки:
(n0, а — постоянные). Можно показать, что в такой среде световой луч имеет форму окружности независимо от того, из какой точки и в каком направлении он вышел.
Это все оптика. Но то же самое и в акустике — уравнение (1) описывает общее свойство лучей для волн любой природы загибаться в сторону уменьшения скорости распространения волны. Если днем на пляже песок раскален, то скорость звука в прилегающем горячем слое воздуха несколько больше, чем вверху (она, как известно, пропорциональна корню квадратному из температуры). В результате, как и в случае оптического миража, «лучи звука» уходят вверх, и голоса на пляже звучат приглушенно. А вечером, когда земля успела уже охладиться, а воздух вверху еще теплый, возникает обратная ситуация — звуки, уходящие вверх, затем загибаются вниз, и песни далеко разносятся в поле.
Впрочем, далеко-то они слышны, а вблизи, может быть, и нет. Во время знаменитых битв, производивших много шума, иногда возникали такие атмосферные условия, при которых образовывалась зона молчания. (Конечно, в эти условия, помимо изменения скорости звука с высотой, входят и наличие облаков, и рельеф местности, и другие тонкости, о которых можно узнать при желании из книг по акустике.) Например, шум битвы при Ватерлоо был слышен на очень большом расстоянии, но не был слышен ближе, где стоял корпус наполеоновского генерала Груши, поэтому последний и не пришел на помощь своему императору. Результат известен. Как, однако, полезно знать физику даже полководцам.