Kvant. Кто-то приближается
Стасенко А.Л. Кто-то приближается? //Квант. — 2001. — № 5. — С. 37-39.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
...сообщения об НЛО уже в большом количестве появляются в середине XIX века,
а в годы II мировой войны появляется масса документальных свидетельств о прямо-таки нашествии НЛО на землю.
Священник Родион. Люди и демоны
Всевозможные «очевидцы» и «контактеры» сообщают о чрезвычайно быстрых и бесшумных перемещениях неопознанных летающих объектов (НЛО). При этом большая часть информации об этих объектах получается в видимом диапазоне спектра (проще говоря, при помощи глаз и, изредка, обычной фотопленки).
А нет ли принципиальной возможности зарегистрировать приближающийся бесшумный НЛО в отсутствие видимости (например, в случае тумана или если НЛО-навтам захочется погасить свои огни)? Какова бы ни была суть этого явления, воспользуемся им для обсуждения законов физики.
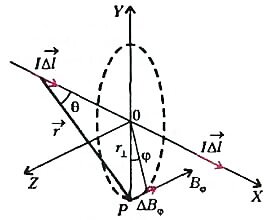
Начнем с бесконечного прямого провода, по которому течет постоянный ток I (рис. 1). Как известно, он порождает магнитное поле, линии индукции которого представляют собою концентрические окружности в плоскостях, перпендикулярных проводу. При этом модуль индукции одинаков во всех точках выделенной окружности радиусом r⊥ (пунктирная линия) и убывает с расстоянием обратно пропорционально этому радиусу:
где индекс φ подчеркивает, что индукция имеет только касательную к окружности составляющую.
Этот вектор индукции \(~\vec B\) можно представить как результат суммирования вкладов от отдельных элементов тока \(~I \Delta \vec l\). На рисунке 1 изображены два таких элемента, симметричных относительно рассматриваемой плоскости. Каждый из этих элементов порождает элементарное поле с индукцией
где θ - угол между направлением элемента тока \(~I \Delta \vec l\) и радиусом-вектором \(~\vec r\), проведенным из этого элемента в точку наблюдения Р. Эта запись отражает закон Био-Савара-Лапласа. Уже одно присутствие стольких замечательных имен говорит о важности закона (2), так что при взгляде на него хочется снять шляпу. В частности, из выражения (2) следует, что индукция пропорциональна самому элементу тока и убывает обратно пропорционально квадрату расстояния до него. Вспомним, кстати, что такой же характер имеет и зависимость напряженности электрического поля точечного заряда (это нам пригодится). Далее, видно, что элемент тока не порождает индукции вдоль своего направления (при θ = 0).
Кто хочет, может просуммировать (проинтегрировать) вклады всех элементов тока и получить из выражения (2) формулу (1). Мы же перейдем к рассмотрению НЛО.
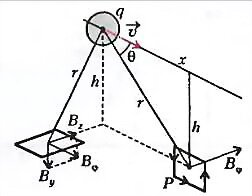
Пусть он имеет формулу шара радиусом a и несет заряд q, двигаясь с постоянной скоростью \(~\vec \upsilon\), параллельной земле (рис.2). Будем вести наблюдение за магнитным полем, порожденным этим движущимся зарядом, в вертикальной плоскости XY, содержащей вектор \(~\vec \upsilon\). Если высота полета h, а расстояние по горизонтали до точки наблюдения х, то \(~r = \sqrt{h^2 + x^2}\) и \(~\sin \theta = \frac hr\). Кроме того, легко видеть (хотя бы из соображений размерностей), что элемент тока можно записать в виде
Тогда магнитное поле в точке Р будет равно
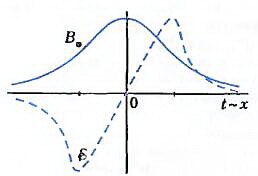
Здесь мы выбрали отсчет времени t таким образом, что значение t = 0 соответствует тому моменту, когда НЛО находится прямо над головой наблюдателя; значит, его приближение соответствует отрицательным значениям t, а удаление - положительным. Качественная зависимость магнитного поля от времени показана на рисунке 3 сплошной линией.
Итак, индукция Bφ зависит от времени! А это значит, что, расположив проволочную рамку вокруг точки Р, мы можем зарегистрировать изменение магнитного поля. Почему? Об этом говорит другой знаменитый закон - закон Фарадея: если изменяется поток магнитной индукции через площадь фиксированного контура, то в последнем наводится электродвижущая сила индукции, пропорциональная скорости изменения этого потока, т.е.
где S - площадь рамки. Знак «минус» свидетельствует еще об одном замечательном факте, способствующем устойчивости Природы: всякая попытка что-то изменить вызывает противодействие. Вот и индуцированная ЭДС такова (см. рис.3), чтобы созданный ею ток порождал магнитное поле, противоположное внешнему растущему полю Bφ, вызванному приближающимся НЛО.
Для численных оценок надо еще уточнить систему единиц и сказать, чему равен электрический заряд НЛО.
Чтобы в предыдущих соотношениях заменить знак пропорциональности на знак равенства, нужно, перейдя к современной Международной системе единиц (СИ), ввести множитель \(~\frac{\mu_0}{4 \pi}\), где μ0 = 4π·10-7 Гн/м - магнитная постоянная. Аналогично, в выражение для напряженности электрического поля точечного заряда q входит множитель \(~\frac{1}{4 \pi \varepsilon_0}\), содержащий электрическую постоянную \(~\varepsilon_0 = \frac{1}{4 \pi \cdot 9 \cdot 10^9}\) Ф/м:
Отметим великолепный факт: если разделить друг на друга эти два множителя, получим
- квадрат скорости света в вакууме! Все это не случайно и стоит глубоких размышлений...
Но что же НЛО? Если он движется в атмосфере Земли, можно оценить его максимальный заряд. Известно, что в сухом воздухе напряженность электрического поля, при которой еще не возникает пробой, равна Emax ~ 3·106 В/м. Подставляя это значение в равенство (5), получим оценку для наибольшего значения электрического заряда, который еще не стекает с шарообразного НЛО:
Собирая все это вместе и (кто может) продифференцировав выражение (4), получим
Но и без дифференцирования можно качественно описать, как изменяется ЭДС индукции в контуре со временем (см. рис.3, пунктир): ε = 0 при t = 0 и достигает самых больших значений в тех точках, где временная зависимость Bφ(t) имеет наибольший наклон.
Тут уже исчерпаны основные физические идеи, и можно заняться численными оценками. Но предоставим эту работу заинтригованным (как мы надеемся) читателям.
Мы же заметим, что необязательно располагать виток проволоки в плоскости полета НЛО. Можно его положить на землю горизонтально где-то сбоку. На рисунке 2 слева изображен такой виток в частном случае - на траверзе пролетающего НЛО. Он тоже пронизывается нормальной составляющей магнитного поля, которая тоже зависит от времени и, значит, тоже порождает ЭДС индукции в контуре.
Тут пора сказать слова типа «Минздрав предупреждает»: «Шутки с НЛО так же плохи, как шутки с черной магией. Это явление делает своими жертвами неврастеников, легковерных и незрелых людей. Легкое любопытство к НЛО может превратиться в разрушительную одержимость... Школьные учителя и другие взрослые не должны поощрять подростков в их увлечении этим предметом» (Джон Киль). Или вот еще: «Что касается так называемых наблюдений за летающими тарелками, то мне кажется, что вероятность психопатологических реакций или индивидуальной, или коллективной истерии... значительно выше, чем вероятность визита инопланетян» (Жан Клод Пекер).
Но при чем тут фантастический НЛО? Разве сверхзвуковой ночной бомбардировщик не является неопознанным летательным аппаратом? Его не видно (ночь) и не слышно (он опережает звук), а включать активные локационные установки нежелательно из-за возможных «точечных ударов», которыми кичатся современные реальные НЛО-навты. А ведь самолет тоже может нести электрический заряд, так что все рассмотренное выше применимо в этом случае.
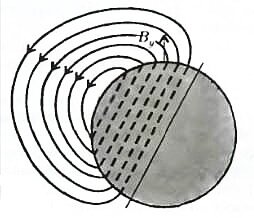
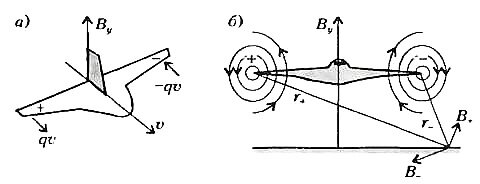
Но пусть даже самолет не заряжен электрически - достаточно того, что он движется в магнитном поле Земли. Это поле качественно изображено на рисунке 4. Видно, что оно имеет вертикальную (радиальную) составляющую By. Значит, при движении со скоростью υx в этом поле на положительный элементарный заряд е действует сила Лоренца, равная Fz = eυxBy и приводящая к возникновению горизонтального (перпендикулярного к By) электрического поля, равного Ez = υxBy (тут индексы указывают направления всех четырех векторов \(~\vec \upsilon\), \(~\vec B\), \(~\vec E\) и \(~\vec F\)). Значит, при размахе крыльев L между концами самолета возникнет разность потенциалов U = υxByL.
Поскольку вблизи географического северного полюса находится южный магнитный полюс, нормальная составляющая магнитного поля Земли в Северном полушарии положительна. Легко видеть, что при этом правое крыло самолета будет заряжено положительно, а левое - отрицательно. (В Южном полушарии — все наоборот.)
Таким образом, даже в случае электронейтрального самолета концы его крыльев приобретут заряды ±q, одинаковые по величине и противоположные по знаку. Вследствие движения самолета, этим зарядам можно поставить в соответствие элементы тока ±qυ (рис.5,а). Каждый из них породит свое магнитное поле, так что в результате получим магнитный диполь (рис.5,б). Линии индукции магнитного поля диполя могут иметь вертикальную составляющую, пронизывающую находящийся на земле проволочный контур и порождающую (вследствие своего изменения во времени) в этом контуре ЭДС.
Конечно, это дипольное поле будет слабее поля движущегося заряда (оно убывает пропорционально r-3, а не r-2); тем не менее, физика указывает на принципиальную возможность зарегистрировать движущийся объект. Остается купить в ближайшем ларьке микроамперметр (еще лучше наноам- перметр, еще лучше... - тут-то и понадобятся численные оценки) и включить его в контур. И тогда ни один НЛО не подберется к вам незамеченным.
Если вам здесь не все понятно - не расстраивайтесь. Даже великие ученые не сразу поняли смысл уравнений Максвелла, описывающих электромагнитные явления. Например, Людвиг Больцман в своих попытках объяснить эти явления изобразил для своих слушателей довольно сложную механическую модель (рис.6). Сейчас нам незачем разбираться в принципе работы этой машины, просто полюбуйтесь ею как историческим курьезом - и, испытывая свои трудности в понимании законов физики, вы почувствуете себя в приличной компании.