Kvant. Легко ли описывать движение
Филонович С.Р. Легко ли описывать движение? //Квант. — 1987. — № 9. — С. 38-40.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Многие понятия кинематики — раздела механики, посвященного изучению движений тел без выяснения их причин,— кажутся нам очень простыми, даже элементарными. Однако потребовались века, чтобы наука выработала эффективные методы описания движений. Остановимся несколько подробнее на истории формирования представлений о двух кинематических величинах — о скорости и ускорении.
Движение любого тела связано с изменением его положения в пространстве с течением времени. Эта привычная для нас мысль не столь уж однозначна. Действительно, что, например, следует принять за независимую переменную при описании движения — путь или время? Ученые начала XVII века не были единодушны в ответе на этот вопрос. И если это различие во взглядах не приводило к серьезным расхождениям при исследовании равномерного прямолинейного движения, то в случае неравномерного движения оно оказывалось весьма существенным. Попробуйте, скажем, установить закон движения, предположив пропорциональность скорости пройденному пути (υ ~ s), и вы убедитесь, что это гораздо более трудная задача, чем описание равноускоренного движения, при котором скорость пропорциональна времени (υ ~ t).
Заслуга систематического рассмотрения задач кинематики прямолинейного равноускоренного движения принадлежит Г. Галилею (1564-1642). Экспериментально изучив свободное падение тел и их движение по наклонной плоскости с малым трением, Галилей сформулировал закон равноускоренного движения, который звучал так: «Если тело, выйдя из состояния покоя, падает равномерно-ускоренно, то расстояния, проходимые им за определенные промежутки времени, относятся между собою как квадраты времен».
Мысль Галилея о том, что свободное падение происходит равноускоренно, воспринималась современниками с трудом. Один из героев книги Галилея «Беседы и математические доказательства» приводит против нее такое, представляющееся ему убедительным, возражение: «Если тяжелое падающее тело выходит из состояния покоя таким образом, что скорость его увеличивается пропорционально времени, истекшему от начала движения, то отсюда следует, что тело должно двигаться с любой степенью скорости или любой большой степенью медленности, выходя из состояния покоя... — явление, которое весьма трудно себе представить, когда наши чувства показывают, что тяжелое падающее тело сразу приобретает большую скорость». Кажущееся противоречие «показаний чувств» и теории Галилей снимает с помощью остроумного опыта (подумайте — какого).
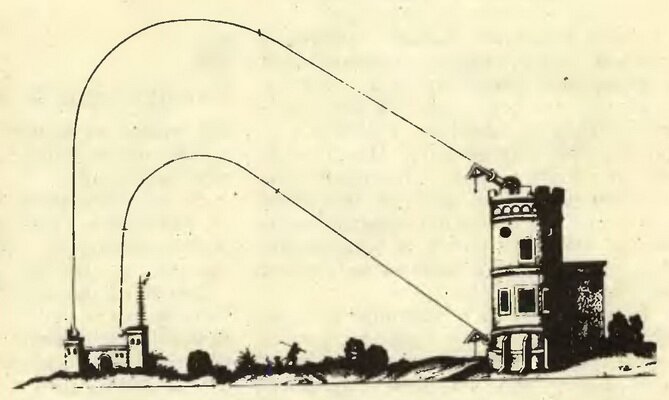
Галилею же принадлежит и идея о представлении сложного движения как результата сложения относительно простых движений. «Пробным камнем» для ее проверки послужила задача о движении тела, брошенного под углом к горизонту, которая (будучи важной в военном отношении) издавна привлекала внимание ученых. Еще Леонардо да Винчи (1452— 1519) в целом правильно представлял вид траектории-такого тела (рис. 1).
Однако и во времена Галилея в трактатах по военному делу можно было встретить ошибочное описание траектории снаряда как совокупности двух отрезков прямых и части окружности (рис. 2).
Доказательство Галилеем теоремы о том, что «при сложном движении, слагающемся из равномерного горизонтального и естественно-ускоренного движений, бросаемое тело описывает полупараболу», представляло крупное научное достижение.
Следует отметить, что Галилей в своих рассуждениях никогда не пользовался понятием «скорость» и. соответствующим выражением \(~\upsilon = \frac{s}{t}\). Все его теоремы посвящены анализу отношений однородных (т. е. имеющих одинаковую размерность) величин. (Вспомним, например, формулировку утверждения, касающегося свободного падения тела.) Такой способ изложения определяется традицией, берущей начало еще в эпохе Античности. Интересно, что и И. Ньютон (1643-1727) в своих знаменитых «Началах» не пользовался выражением \(~\upsilon = \frac{s}{t}\). Первым, кто осмелился ввести скорость таким образом, был Л. Эйлер (1707—1783). В сочинении «Теория движения твердых тел». (1765 г.) он дал ей такое определение: «При равномерном движении отношение путей к промежуткам времени, в течение которых они проходятся, называется быстротой или скоростью. <...> Итак, если при равномерном движении за время, равное t, проходится путь, равный s, то скорость равна \(~\frac{s}{t}\). Если скорость обозначить буквой υ, то \(~\upsilon = \frac{s}{t}\)». Как видите, даже обозначения переменных, использованные Эйлером, сохранились до наших дней.
Но, может быть, мы преувеличиваем значимость шага, сделанного Эйлером? Скорее всего, нет. Насколько необычным для XVIII века был его подход к определению физической величины, свидетельствуют пояснения, которые Эйлер счел необходимым сделать далее: «Здесь может, пожалуй, возникнуть сомнение по поводу того, каким образом можно делить путь на время, так как ведь это — величины разнородные, и, следовательно, невозможно указать, сколько раз промежуток времени, например, в 10 минут, содержится в пути длиной, например, в 10 футов. <...> Если для измерения путей мы изберем определенную длину в качестве единицы и точно так же для времени изберем в качестве единицы определенный промежуток времени и если мы будем постоянно пользоваться этой мерой, то все пути и времена выразятся в отвлеченных числах, и тогда для деления первых на вторые не будет никаких препятствий». Вот какие простые вещи приходилось разъяснять в фундаментальных сочинениях по механике в середине XVIII века.
Но и Эйлера нельзя считать в полной мере автором современного определения скорости — он не пользовался понятием скорости как вектора, а отдельно определял модуль скорости и ее направление. Представление о скорости как о направленном отрезке вошло в физику примерно через сто лет после публикации сочинения Эйлера, когда в математике были разработаны основы векторного исчисления.
После рассказа о длинной и сложной истории понятия скорости уже не столь удивительным представляется тот факт, что понятие ускорения вошло в науку еще позже. Впервые физическую величину «ускорение» ввел в своих лекциях по механике французский математик и инженер Ж. Понселе (1788-1867) лишь в 1841 году. Это не значит, однако, что в сочинениях авторов XVIII и даже XVII веков не встречается термин «ускорение». Им пользовались, но подразумевали не физическую величину, а процесс изменения скорости. (Отметим попутно, что в физике можно найти и другие примеры такого смешанного словоупотребления — вспомним хотя бы термины «перемещение», «давление», «сопротивление».) Правда, Эйлер уже рассматривал вторую производную пути по времени, имеющую с современной точки зрения смысл касательного ускорения, но он интерпретировал ее по-другому. Эйлер писал, что эта производная «выражает собою тот отрезочек пути, на который тельце перемещается сверх того расстояния, которое пройдено им в силу бывшего у него раньше движения».
Широкое использование ускорения в работах по механике началось лишь после выхода в свет (1851 г.) сочинения «Элементы механики» француза А. Резаля, ученика Понселе.
Итак, история основных понятий кинематики показывает, что выработка научного языка для описания движения потребовала преодоления многих трудностей принципиального характера. И то, что мы теперь с легкостью пользуемся этим языком, лишний раз подчеркивает заслуги ученых прошлого.
Смотреть HD
видео онлайн
бесплатно 2022 года