Kvant. Лучи и волны
Кикоин А.К. Лучи и волны //Квант. — 1985. — № 11. — С. 23-24.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Содержание
В начале XIX века, благодаря работам по интерференции и дифракции света, окончательно утвердилось представление о том, что распространение света в пространстве представляет собой волновой процесс. Однако задолго до этого возникла, сформировалась и продолжает существовать и в наши дни так называемая геометрическая оптика. В этом разделе физики изучаются законы распространения света на основе представлений о световых лучах. Говорится о падающих, отраженных и преломленных лучах, о расходящихся, сходящихся и параллельных пучках лучей и т. п.
«Лучевая» картина света позволяет описать многое из того, что происходит, когда свет падает на зеркала, призмы или линзы («Физика 10», глава 6). При этом говорится о ходе лучей, например в призме, линзе или какой-то более сложной оптической системе.
Значит ли это, что через призмы и линзы проходят не световые волны, а лучи, что от зеркал отражаются не волны, а лучи? Что представляют собой световые лучи? Какова их физическая сущность?
Оказывается, за лучами не кроется никакой физической реальности. Световые лучи — это линии, вдоль которых распространяется световая волна. Все законы геометрической оптики могут быть получены из волновой теории как предельный случай, когда размеры препятствий на пути света много больше длины световой волны. Таким образом, использование понятия светового луча вовсе не обязательно для понимания того, что происходит при распространении света. Оно просто облегчает рассмотрение.
Убедимся в этом на нескольких конкретных примерах.
Призма
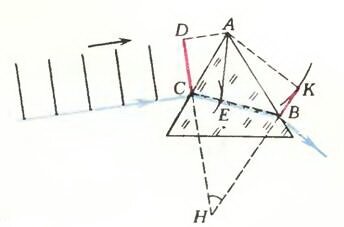
Пусть на стеклянную призму треугольного сечения, находящуюся в воздухе (рис. 1), падает плоская световая волна. В какой-то момент времени волновая поверхность (волновой фронт) достигнет в точке С поверхности призмы.
Начиная с этого момента, нижний край выбранного нами участка DC волновой поверхности (точнее, участка линии пересечения волновой поверхности с плоскостью чертежа) распространяется в стекле, в то время как верхний продолжает еще распространяться в воздухе. Когда верхний конец (точка D) достигнет призмы в точке А, сферическая волна, распространяющая от нижнего конца (точка С), дойдет до точки Е, причем расстояние СЕ будет примерно в полтора раза меньше, чем DA, так как скорость света в стекле приблизительно в полтора раза меньше, чем в воздухе. Далее сферическая волна, центром которой является точка С, достигнет второй грани призмы в точке В. В свою очередь из точки А тоже будет распространяться сферическая волна. К тому моменту, когда волна в стекле распространится на расстояние ЕВ, волна из А пройдет больший путь (скорость света в воздухе больше, чем в стекле!). Таким образом, новым фронтом волны по другую сторону призмы (вернее, участком линии его пересечения с плоскостью чертежа) станет отрезок ВК. Значит, роль призмы состоит в том, что фронт CD световой волны преобразовался в ВК. И произошло это потому, что скорость света в стекле меньше, чем в воздухе.
Такова волновая картина прохождения света через призму. Для сравнения на этом же рисунке синим цветом показана также и обычно приводимая картина хода луча в призме (см., например, § 56 «Физики 10»). Из рисунка 1 видно, что лучи — это просто прямые, перпендикулярные волновым поверхностям (волновым фронтам). «Преломление лучей света» в действительности означает поворот фронта волны. Угол поворота волнового фронта — это ∠ СНВ. Таков же, очевидно, и угол преломления лучей.
Как видно, «лучевая» картина проще, чем «волновая», поэтому обычно ею и пользуются.
Собирающая линза
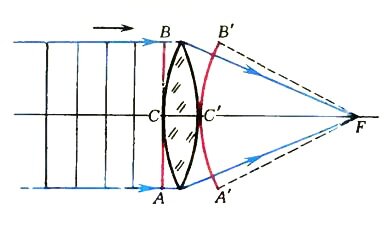
Пусть на двояковыпуклую стеклянную линзу, находящуюся в воздухе, падает плоская световая волна (рис. 2).
С того момента, когда волновая поверхность (точнее, выбранная ее часть) коснется своей серединой первой поверхности линзы в точке С, путь всех ее точек (кроме середины) проходит частью в воздухе, а частью в стекле. По мере удаления от середины волнового фронта к его краям доля «стеклянной» части пути уменьшается, поэтому, когда середина волны достигнет в точке С’ второй поверхности линзы, все остальные участки волнового фронта продвинутся на большее расстояние (самое большое расстояние пройдут крайние точки). В результате получается, что по выходе из линзы плоский волновой фронт АСВ превратится в сферический А’С’В’. Центр этой сферической волны — точка F — называется, как известно, фокусом линзы. Понятно, что если, наоборот, сферическая волна выходит из точечного источника, расположенного в фокусе линзы, то после линзы она преобразуется в плоскую волну.
Синим цветом на рисунке 2 показан ход лучей в собирающей линзе.
Рассеивающая линза
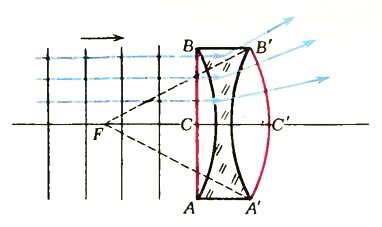
Рисунок 3 иллюстрирует случай, когда плоская волна падает на двояковогнутую стеклянную линзу, находящуюся в воздухе.
После того как волновая поверхность коснется в точках А и В линзы, крайние участки будут отставать от других частей волнового фронта (так как проходят в стекле, где скорость света меньше, чем в воздухе). В результате плоская волна АСВ превратится в сферическую А’С’В’. Но центр этой сферической волны (точка F) находится по ту же сторону от линзы, откуда пришла плоская волна. Точку F тоже называют фокусом линзы, но фокусом мнимым, так как преломленный свет сюда реально не попадает. Синим цветом и здесь показан соответствующий ход лучей.
Читатель без труда сумеет сам построить волновые картины прохождения света через линзы, когда на них падают не плоские, а сферические волны. После прохождения линзы они преобразуются в сферические же волны, но с другими радиусами. Из таких картин можно получить и формулу линзы, такую же, разумеется, как и из геометрической оптики.
Смотреть HD
видео онлайн
бесплатно 2022 года