Kvant. Откуда течет энергия
Ромишевский Е., Стасенко А.Л. Откуда течет энергия: открытие за открытием //Квант. — 2003. — № 5. — С. 31,34-35.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Где только возможно, знание должно
быть внедряемо в ум другого тем самым
путем, каким оно было впервые открыто.
Бэкон
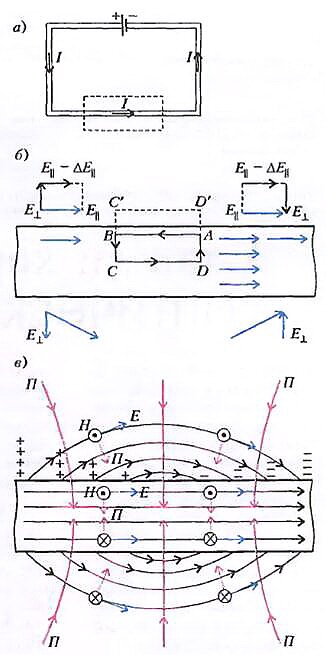
Рассмотрим самую что ни на есть простую электрическую цепь - батарейку, электроды которой замкнуты проводом, обладающим некоторым конечным сопротивлением (рис. 1,а). Разумеется, в проводе будет течь постоянный электрический ток, и будет постоянно выделяться джоулево тепло. Тут еще (или уже) нет открытий. Чтобы их сделать, надо потрудиться. Поэтому вспомним основные свойства электромагнитного поля.
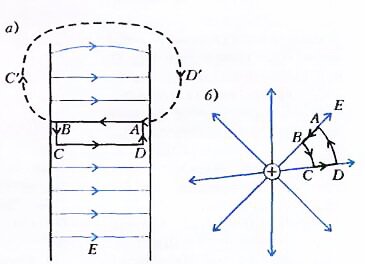
Самым «простым» полем иногда считается электрическое поле плоского конденсатора (рис.2,а). Поскольку оно пространственно однородно, то, протащив любой заряд +q по замкнутому контуру ABCDA, мы получим нулевую работу. Действительно, на участке АВ работа будет равна -qE · АВ (поле сопротивляется перемещению заряда), на участке CD поле совершает работу +qE · CD = +qE · АВ, а на участках ВС и DA работа не совершается вовсе. В этом же можно убедиться и на примере точечного заряда (рис.2,б). И вообще, это свойство любого потенциального поля: работа поля по замкнутому контуру (или циркуляция поля) равна нулю. В качестве другого аналогичного примера может служить поле тяготения. Можно показать, что свойство потенциальности поля не зависит ни от формы контура, ни от направления его обхода - ноль он и в Африке ноль.
Однако, не так уж он прост, этот плоский конденсатор (поэтому выше эта его простота взята в кавычки). Ведь если мы захотим пройти по контуру ABC’D’A , то из потенциальности электростатического поля мы должны будем сделать заключение, что на внешнем участке контура C’D’ тоже должно быть поле, в точности компенсирующее нашу работу на участке АВ. Поэтому, когда говорят о том, что поле плоского конденсатора однородно и локализовано внутри, часто произносят извиняющие слова типа «далеко от концов пластин», «расстояние между пластинами много меньше их линейных размеров» или даже «возьмем бесконечно большие пластины» (хотя это и очень нелегко).
Но мы можем извлечь из плоского конденсатора еще один полезный факт. Если, действительно, взять участок АВ далеко от краев пластин, то замыкающий внешний участок контура C’D’ будет очень длинным и, значит, среднее значение напряженности поля вдоль него будет малым, а «в пределе», если пластины бесконечно велики, это значение будет стремиться к нулю. Отсюда получим другое важное утверждение: скачок нормальной (перпендикулярной) составляющей электростатического поля при прохождении заряженной плоскости (а это и есть пластина конденсатора) пропорционален поверхностной плотности заряда σ:
Все это нам немедленно пригодится. Рассмотрим увеличенный отрезок провода (рис. 1,б). Поскольку ток течет параллельно оси, электрическое поле внутри провода тоже параллельно оси. Плотность тока \(~\vec j\) связана с напряженностью поля \(~\vec E\) в любой точке локальным законом Ома \(~\vec j = \lambda \vec E\), где λ - удельная электропроводность материала. Если мы пройдемся вдоль контура ABCDA внутри провода, то, опять же из условия равенства циркуляции поля нулю, сделаем вывод о том, что вдоль CD и ВА поле \(~\vec E\) должно быть одинаково. Значит, ток тоже равномерно распределен по сечению проводника, т.е. \(~\vec j = \operatorname{const}\), так что \(~I = j \pi a^2\) (где a - радиус поперечного сечения провода). Но по той же причине, пройдясь вдоль контура ABC’D’A, мы заключим, что продольная составляющая электрического поля E|| вдоль отрезка C’D’, лежащего вне провода, должна быть такой же, как и внутри провода. Получается, что снаружи провода есть электрическое поле. (Чем не открытие?!)
Далее, интуитивно ясно, что с удалением от провода напряженность поля будет уменьшаться. Но ведь его циркуляция по любому контуру должна оставаться нулевой. Как это себе представить? Очень просто: это означает, что вне провода существует и перпендикулярная (радиальная) составляющая E⊥, направленная либо вверх, либо вниз, но в любом случае -«помогающая» более слабому полю E|| - ΔE|| (более удаленному от провода) компенсировать вклад в циркуляцию более сильного поля E||. Таким образом, получается, что вне провода линии электрического поля \(~\vec E\), вообще говоря, наклонены к его оси. В результате получится картина, представленная на рисунке 1,в.
Но что это? Внутри провода поле \(~\vec E\) строго параллельно оси, следовательно, не имеет радиальной составляющей, а снаружи есть составляющая, перпендикулярная поверхности провода. Значит, существует скачок нормальной составляющей электрического поля при переходе через поверхность провода. А это означает, что существуют поверхностные заряды. В целом провод, конечно, нейтрален: ведь батарейка не может создать электрический заряд, а может только перераспределить его.
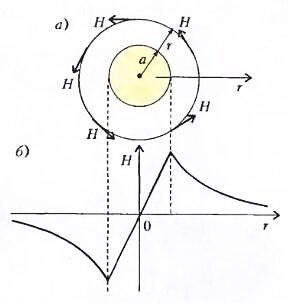
Но что это мы все об электрическом поле? А магнитное? Ведь если течет ток, то вокруг него образуется кольцевое магнитное поле. Как вы знаете, силовой характеристикой магнитного поля является его индукция \(~\vec B\). Но, по аналогии с электрическим полем, наряду с индукцией говорят и о напряженности магнитного поля \(~\vec H\). Для вакуума связь между этими характеристиками предельно проста\[~\vec B = \mu_0 \vec H\], где μ0 - магнитная постоянная. Напряженность магнитного поля удовлетворяет своему закону: циркуляция по замкнутому контуру равна току, охватываемому этим контуром (рис. 3,а):
Отсюда видна, во-первых, размерность магнитной напряженности: [H] = А/м. Во-вторых, видно, что значение индукции вне провода убывает с расстоянием от провода:
В-третьих, если мы возьмем контур внутри провода (r < a), то должны записать
(справа как раз и стоит ток, протекающий через площадку πr2, - вспомним, что j = const). Отсюда
В результате получим радиальное распределение окружной составляющей магнитного поля, изображенное на рисунке 3,б.
Важно, что в любой точке пространства (внутри и вне провода) поля \(~\vec E\) и \(~\vec H\) взаимно перпендикулярны.
Итак, мы знаем уже достаточно много, чтобы приступить к Основному Открытию.
Что получится, если векторно перемножить напряженности обоих полей - электрического и магнитного? Получим новую физическую величину, размерность которой есть
Но ведь это размерность плотности потока энергии! (Вспомним, что плотность тока, равная плотности потока заряда, имеет размерность [j] = Кл/с·м2, плотность потока массы имеет размерность кг/с·м2 и т.д.) Исторически эта величина называется вектором Умова-Пойнтинга \(~\vec \Pi\). Но если это вектор, то куда он направлен? Конечно, перпендикулярно обоим векторам \(~\vec E\) и \(~\vec H\) (а не вдоль одного из них - чтобы другому не было обидно). Причем так, что векторы \(~\vec E\), \(~\vec H\) и \(~\vec \Pi\) образуют правую тройку, как оси х, у и z. (Это очень похоже и на расположение векторов в электромагнитной волне, которая потому и называется поперечной, что \(~\vec E\) и \(~\vec H\) в ней перпендикулярны направлению ее распространения, т.е. тому направлению, в котором течет энергия волны.) Взаимное расположение этих векторов и их векторные линии качественно изображены на рисунке 1,в.
Заметим, что внутри провода вектор \(~\vec \Pi\) направлен строго к оси, поскольку там поле \(~\vec E\) параллельно оси. Кроме того, на оси его величина равна нулю, поскольку в произведение входит множитель H, обращающийся в ноль на оси (см. рис.3,б).
Что же получается? Плотность потока энергии во всем пространстве течет к проводу, а затем направляется кратчайшим путем к его оси, погибая на расстоянии, равном его радиусу? Но энергия не может бесследно исчезнуть. И действительно, она просто превращается в другой вид - тепло. Это и есть джоулевы потери.
Возьмем участок провода длиной l, на концах которого разность потенциалов равна U. Поскольку у поверхности провода напряженности магнитного и электрического полей равны, соответственно,
то плотность потока энергии через поверхность площадью 2πal внутрь провода равна
Если еще учесть, что \(~I = \frac UR\) (где R - сопротивление этого участка провода), то правую часть последнего равенства можно записать и в виде
Все эти формулы для тепловой мощности хорошо знакомы каждому здравомыслящему школьнику. Это еще раз убеждает, что «все в порядке».
А откуда же берется этот поток энергии во всем пространстве? Иные студенты отвечают в духе модных оккультистов: из Космоса. Ну и замечательно, тогда не нужны ветряные мельницы, двигатели внутреннего сгорания, электростанции - в Космосе энергии сколько угодно. А иные считают, что энергия от источника к потребителю течет внутри провода вдоль его оси. Для них описанная картина полей и потока энергии действительно может служить полезным открытием.
И последнее открытие. Если энергия электромагнитного поля погибает в проводе, превращаясь в тепло, то зачем нужны провода? Долой их?! И не нужны миллионы тонн меди и алюминия, и нет никаких потерь?!
Увы, это открытие не состоится. Действительно, пространственная структура электрического и магнитного полей такова, как мы изобразили. Действительно, энергия течет извне и «пропадает»' внутри провода. Но ее линии тока идут, конечно, из той батарейки, которая гонит электрический ток (попробуйте изобразить это самостоятельно). И провода нужны как раз для того, чтобы создать именно такое распределение плотности потока энергии в пространстве. А тепловые потери - это плата за передачу энергии.
Кстати, что если мы разделим произведение ЕН на скорость света? Получится новая величина с размерностью Дж/м3. Естественно назвать ее объемной плотностью энергии (вспомним о массовой плотности, размерность которой кг/м3). Выходит, вектор Умова-Пойнтинга указывает, куда и с какой скоростью перемещается плотность энергии.
И еще. Что если в нашу схему (см. рис. 1,а) вставить ключ и замкнуть его в некоторый начальный момент? Тогда потечет переменный ток, и мы перейдем от электромагнитостатики к электромагнитной динамике. А это уже другой разговор, который можно продолжить на физическом факультете МГУ или в Московском физико-техническом институте. Чего вам и желаем!