Слободянюк А.И. Физика 10/11.7
§11. Постоянный электрический ток
11.7 Примеры расчета сопротивлений цепи.
Пользуясь полученными правилами расчета последовательного и параллельного соединения, можно рассчитать сопротивление сложной цепи, содержащей резисторы, соединенные различными комбинированными способами. Для этого необходимо последовательно заменять участки цепи (последовательного, параллельного соединения) эквивалентными сопротивлениями.
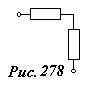
Подчеркнем, что вид соединения определяется порядком протекания электрического тока, а не тем как элементы расположены в том или ином приборе, и тем более не тем, как они изображены на схеме. Так два резистора, показанные на рис. 278 соединены последовательно, а не перпендикулярно!
Рассмотрим несколько примеров расчета сопротивлений разветвленных цепей.
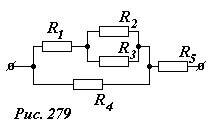
Рассчитаем сопротивление цепи, изображенной на рисунке 279. Для упрощения расчетов и экономии места положим, что сопротивления всех резисторов одинаковы и равны R.
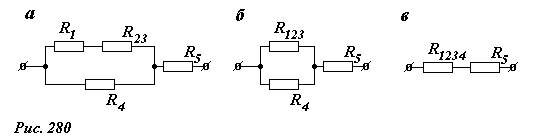
Будем шаг за шагом упрощать схему, заменяя ее части эквивалентными сопротивлениями (Рис 280).
Резисторы R2 и R3 соединены параллельно, поэтому их общее сопротивление равно \(~R_{23} = \frac{1}{2} R\) (рис. 280а); резисторы R1 и R23 соединены последовательно, следовательно, их сопротивление \(~R_{123} = R_1 + R_{23} = R + \frac{1}{2} R = \frac{3}{2} R\) (рис. 280б); для расчета параллельно соединенных резисторов R123 и R4 (рис. 280 в) воспользуемся формулой
наконец, этот резистор последовательно соединен с резистором R5, поэтому общее сопротивление исходной цепи равно \(~R_{ob} = R_{1234} + R_5 = \frac{3}{5} R + R = \frac{8}{5} R\).
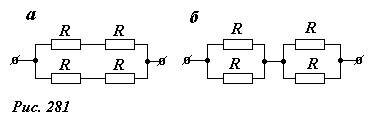
Рассмотрим теперь две схемы, изображенные на рисунке 281. Элементарные расчеты, которые можно провести в уме, приводят к результату: сопротивления обеих цепей равны R.
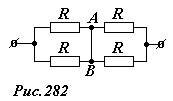
Зададимся вопросом, является ли это совпадение случайным? Схема а, превращается в схему б, если соединить проводником точки А и В (рис. 282). Однако из симметрии схемы следует, что электрический ток по этому проводнику АВ не пойдет. Действительно, в какую сторону ему идти? – оба направления равноправны. Еще одним доказательством отсутствия тока в этом проводнике является равенство потенциалов точек А и В.
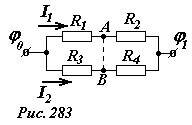
Рассмотрим общую схему такого соединения с произвольными значениями сопротивлений резисторов (рис. 283) и вычислим потенциалы точек А и В. Сила тока через последовательно соединенные резисторы R1 и R2 определяется законом Ома
Разность потенциалов на резисторе R1 равна
поэтому потенциал точки А равен
Аналогичные рассуждения для нижней ветви цепи позволяют записать потенциал точки В
Итак, условие отсутствия тока между точками А и В при их соединении точек, следующее из равенства потенциалов \(\varphi_A = \varphi_B\) , имеет вид
Рассмотренная схема называется мостиком Уитсона, а условия (1) – условием уравновешенности (или сбалансированности) моста. Подобные схемы широко используются в различных электроизмерительных устройствах.
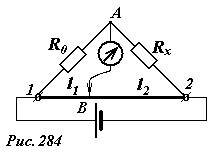
Простейший пример такого использования показа на рис. 284. Кусок однородной проволоки (1-2) с достаточно высоким удельным сопротивлением натянут на измерительную линейку, параллельно ей подключают два резистора, сопротивление одного из них R0 известно, сопротивление второго Rx измеряется. К образованной таким образом мостовой схеме подключается источник тока. К точке соединения резисторов А, подключен чувствительный гальванометр [1], второй вывод которого с помощью скользящего контакта В подключается к проволоке. Передвигая контакт по проволоке, добиваются того, чтобы ток через гальванометр прекратился. В этом случае мот оказывается уравновешенным. Так как сопротивление проволоки пропорционально ее длине, то условие уравновешенности (1) в данном случае имеет вид
из которого легко определить неизвестное сопротивление, по измерению длин частей проволоки. В данной схеме электрическое сопротивление измеряется, фактически, с помощью линейки. Помимо простоты данной схемы, ее достоинством является отсутствие необходимости измерять значение силы тока, достаточно убедится в его отсутствии, что может быть сделано с высокой точностью. Подобный метод измерения называется «нулевым».
В некоторых случаях точки цепи, имеющие одинаковый потенциал, определяются просто, исходя из симметрии схемы. В таких ситуациях расчет электрического сопротивления значительно упрощается: во-первых, если такими точками включены элементы цепи, то их можно отбросить, так как электрический ток через них не течет; во-вторых, точки равного потенциала можно соединить проводником – это не приведет к изменению сопротивления, так как распределение токов в цепи не изменится.
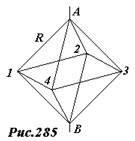
Рассчитаем, например, сопротивление каркасного октаэдра [2], изготовленного из проволоки, сопротивление каждого ребра которого равно R (рис. 285). При подключении источника тока к противоположным вершинам А и В, точки 1,2,3,4 равноправны, поэтому имеют одинаковый потенциал. Следовательно, ток не течет по ребрам октаэдра, соединяющим эти вершины, поэтому, их можно отбросить, не нарушая распределения токов по остальным ребрам. Тогда сопротивление каркаса становится эквивалентным сопротивлению четырех параллельно соединенных ветвей, состоящих из двух ребер, общее сопротивление равно \(~\frac{R}{2}\) .
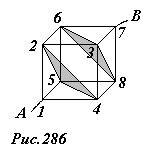
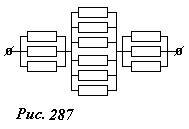
Найдем сопротивление проволочного куба, сопротивление каждого ребра которого равно R, при подключении источника тока к противоположным вершинам А и В (рис. 286). Вершины куба 2,4,5 находятся на расстоянии одного ребра от точки «входа» А, поэтому их потенциалы равны, следовательно, их можно соединить между собой, не нарушая при этом распределения токов по ребрам куба. Аналогично, можно соединить между собой вершины 3,6,8. Таким образом, точка А оказывается соединенной с «объединенной точкой 2,4,5» тремя параллельно соединенными ребрами, от «точки 2,4,5» до «точки 3,6,8» включено параллельно шесть ребер, и далее до выхода, точки В, еще три параллельно соединенных ребра. Таким образом, получаем эквивалентную схему рассматриваемого каркаса (рис. 287), общее сопротивление которой рассчитывается элементарно