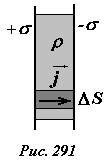Слободянюк А.И. Физика 10/11.9

Содержание книги

Предыдующая страница

§11. Постоянный электрический ток

11.9 Время установления стационарного тока.

В окружающем мире ничто не происходит мгновенно – всякому стационарному процессу предшествует процесс установления, имеющий конечную длительность. Оценка характерных времен установления стационарного режима необходима для анализа применимости различных упрощающих моделей, в частности стационарных. Процессы перехода в стационарный режим часто называют переходными или релаксационными. В данном разделе мы обсудим некоторые факторы, влияющие и определяющие длительность таких процессов для электрического тока.

Время распространения электрического поля определяется скоростью света и размерами рассматриваемой электрической цепи. Мы уже отмечали, что при подключении проводящей цепи к источнику первоначально проходит процесс распространения электрического поля вдоль цепи. Само же электрическое поле распространяется вдоль проводов со скоростью близкой к скорости света c ≈ 3·10⁸ м/с. Поэтому время установления электрического поля вдоль цепи длиной l оценивается как

\(~\tau_1 = \frac{l}{c}\) . (1)

Так если электрическая осветительная лампочка находится на расстоянии 10 метров от выключателя, то после его замыкания, электрическое поле достигает лампочки через время τ ≈ 3·10^-8 с. Скорость света велика настолько, что если выключатель расположить на северном полюсе Земли, а лампочку на южном, то поле достигнет лампочку через время меньшее 0,1с (учитывая, что длина меридиана приблизительно равна 20000 км = 2·10⁷ м).

Закон Ома описывает установившееся движение заряженных частиц. Прежде чем эти частицы начнут двигаться с постоянной скоростью (в среднем), они разгоняются. Время разгона заряженных частиц определяется массой частиц и тормозящей силой. Для оценки этого времени воспользуемся рассмотренной моделью движения электронов в металле, в рамках которой считается, что на движущиеся электроны действует тормозящая сила, пропорциональная скорости движения. В рамках этой модели уравнение второго закона Ньютона имеет вид (с сохранением всех прежних традиционных обозначений)

\(~ma = eE - \beta \upsilon\) .

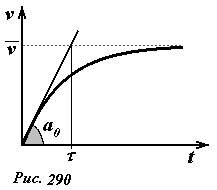
Движение, описываемое этим уравнением, не является ни равномерным, ни равноускоренным. Пусть в начальный момент времени скорость электрона равна нулю υ₀ = 0, тогда он начинает двигаться с ускорением \(~a_0 = \frac{eE}{m}\) , по мере роста скорости ускорение уменьшается, наконец, когда тормозящая сила уравновесит силу, действующую со стороны электрического поля, ускорение обратится в нуль, и дальнейшее движение будет проходить с постоянной установившейся скоростью \(~\bar{\upsilon} = \frac{eE}{\beta}\) (рис. 290). Для оценки характерного времени разгона можно принять, что скорость нарастает с ускорением a₀ от нуля до установившегося значения, поэтому это время равно

\(~\tau_2 = \frac{\bar{\upsilon}}{a_0} = \frac{m}{\beta}\) . (2)

Заметим, что использованный метод получения оценок является традиционным для многих подобных задач.

Модельный параметр β выражается через характеристики проводника посредством формулы для удельного электрического сопротивления, полученной нами ранее

\(~\rho = \frac{2m}{e^2 n \tau} = \frac{\beta}{e^2 n}\) . (3)

Таким образом, время разгона электронов в металле оценивается формулой

\(~\tau_2 = \frac{m}{\beta} = \frac{m}{e^2 n \rho}\) . (4)

Обратите внимание, что полученный результат не зависит от напряженности электрического поля, действующего на электрон. Так для меди (концентрация свободных электронов для которой n ≈ 8·10²⁸ м^-3, а ρ ≈ 1,7·10^-8 Ом·м) время разгона равно

\(~\tau_2 = \frac{9 \cdot 10^{-31}}{(1,6 \cdot 10^{-19})^2 \cdot 8 \cdot 10^{28} \cdot 1,7 \cdot 10^{8}} \approx 3 \cdot 10^{-14} c\) . (5)

Полученное время настолько мало, что экспериментально его зарегистрировать невозможно, поэтому временем разгона электронов практически всегда можно пренебречь. Малость полученного времени во многом обусловлена малостью массы электрона.

Для наглядного представления о полученной длительности укажем, что за такой промежуток времени свет проходит расстояние порядка 10^-7 м, которое приблизительно равно толщине человеческого волоса.

Интересно отметить, что характерное время разгона по порядку величины совпадает со средним временем свободного движения электрона между столкновениями. Это время легко выразить из формулы (3) \(~\tau = \frac{2m}{e^2 n \rho}\) .

Задания для самостоятельной работы.

1. Оцените время разгона иона Na⁺ в 10% растворе поваренной соли в воде. Удельное электрическое сопротивление такого раствора приблизительно равно ρ ≈ 8·10^-2 Ом·м.
2. Из формулы (4) следует, что для сверхпроводников (для которых ρ = 0) время разгона электронов стремится к бесконечности. Объясните данный результат.

Изучив основные законы движения заряженных частиц в веществе, можно оценить применимость электростатических моделей. Так, при изучении поведения веществ в электрическом поле, мы говорили, что в проводниках очень быстро устанавливается равновесное распределение индуцированных зарядов на его поверхности. Диэлектриками мы назвали вещества, которые не проводят электрический ток. Однако все вещества в той или иной степени проводят электрический ток, поэтому граница между проводниками и диэлектриками условна. Сейчас мы можем дать количественный критерий возможности использования моделей идеальных проводников (веществ, электрическим сопротивлением можно пренебречь) и идеальных диэлектриков (веществ, проводимостью которых можно пренебречь). Для этого нам необходимо оценить время установления равновесного распределения индуцированных зарядов.

Для этого рассмотрим следующую систему: пространство между двумя параллельными хорошо проводящими пластинами заполнено однородным веществом с удельным электрическим сопротивлением ρ (рис. 291), то есть представляет собой обыкновенный плоский конденсатор. Пусть в начальный момент времени на пластинах равномерно распределены электрические заряды с поверхностными плотностями +σ и -σ. Оценим время, за которое конденсатор разрядится, то есть электрические заряды перетекут через слой вещества. Пренебрегая диэлектрическими свойствами заполняющего вещества, напряженность однородного электрического поля внутри конденсатора может быть описана формулой \(~E = \frac{\sigma}{\varepsilon_0}\) , тогда по закону Ома плотность электрического тока будет равна

\(~j = \frac{1}{\rho} E = \frac{\sigma}{\varepsilon_0 \rho}\) . (6)

Выделим в конденсаторе небольшой цилиндр, основания которого лежат на пластинах и имеют площадь ΔS. Сила электрического тока, протекающего по цилиндру равна \(~I = j \Delta S = \frac{\sigma}{\varepsilon_0 \rho} \Delta S\). Этот ток равен скорости уменьшения электрического заряда \(~q = \sigma \Delta S\) на основаниях цилиндра. Поэтому изменение поверхностной плотности заряда описывается уравнением

\(~\frac{\Delta q}{\Delta t} = -I\) , или \(~\frac{\Delta \sigma}{\Delta t} = -\frac{\sigma}{\varepsilon_0 \rho}\) . (7)

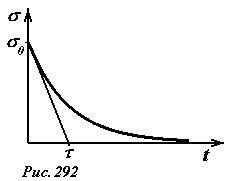
Как следует из этого уравнения, скорость уменьшения заряда пропорциональна поверхностной плотности заряда. Поэтому в начальный момент времени, когда плотность заряда σ₀ максимальна, скорость уменьшения заряда также максимальна и равна \(~j_0 = \left (\frac{\Delta \sigma}{\Delta t} \right )_0 = -\frac{\sigma_0}{\varepsilon_0 \rho}\). Далее по мере уменьшения зарядов на пластинах, скорость разрядки (равная плотности тока) будет уменьшаться (см. рис. 292). Оценку характерного времени разрядки можно получить, полагая, что поверхностная плотность уменьшается от σ₀ до нуля с постоянной скоростью разрядки j₀. Таким образом, получаем интересующее нас время

\(~\tau_3 = \frac{\sigma_0}{j_0} = \varepsilon_0 \rho\) . (8)

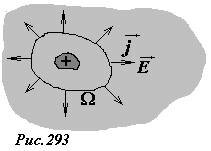
Эта важная формула может быть получена и в более общем случае. Предположим, что внутри большого тела, изготовленного из однородного вещества с удельным электрическим сопротивлением ρ возникла малая область, имеющая электрический заряд q (рис. 293). Уменьшение заряда этой области связано с его растеканием по всему объему тела. Окружим рассматриваемую заряженную область замкнутой поверхностью Ω. Сила электрического тока пересекающего через эту поверхность, равна скорости уменьшения заряда внутри поверхности. Эта сила тока равна потоку вектора плотности тока через поверхность \(~I = \Phi_{\vec j}\). Так как по закону Ома плотность тока пропорциональна напряженности электрического поля \(~\vec j = \frac{1}{\rho} \vec E\), то потоки этих векторов связаны аналогичным соотношением \(~\Phi_{\vec j} = \frac{1}{\rho} \Phi_{\vec E}\). Поток вектора напряженности электрического поля определяется теоремой Гаусса \(~\Phi_{\vec E} = \frac{q}{\varepsilon_0}\). Таким образом, величина заряда внутри рассматриваемой области подчиняется уравнению

\(~\frac{\Delta q}{\Delta t} = -I = -\Phi_{\vec j} = -\frac{1}{\rho} \Phi_{\vec E} = -\frac{q}{\varepsilon_0 \rho}\) ,

которое полностью совпадает с уравнением (7), поэтому время растекания заряда также оценивается формулой (8).

Полученная нами оценка времени установления зарядов на проводнике называется максвелловским временем релаксации. Мы уже указывали, что удельные электрические сопротивления веществ изменяются в очень широких пределах, соответственно изменяются и времена установления зарядов на них. Так для хороших проводников, например меди, это время равно

τ₃ = 1,7·10^-8 Ом·м · 8,85·10^-12 Ф/м ≈ 1,5·10^-19 с .

Это время чрезвычайно мало, поэтому для таких вещества при описании электростатических явлений с высокой степенью точности можно считать идеальными проводниками.

В качестве противоположного примера (изолятора) возьмем широко известный полиэтилен, для которого ρ ≈ 10¹⁵ Ом·м , соответственно, максвелловское время релаксации τ₃ = 10¹⁵ Ом·м · 8,85·10^-12 Ф/м ≈ 10⁴ с ≈ 3 час. Поэтому если вам необходимо рассматривать процессы, протекающие в полиэтилене в течение нескольких минут, то с высокой степенью точности полиэтилен можно считать идеальным диэлектриком (изолятором). Для веществ, имеющих удельное сопротивление порядка 10¹¹ - 10¹² Ом·м (сухая древесина, резина, некоторые виды стекол и пластмасс), максвелловское время составляет от десятых долей секунды до нескольких секунд.

Таким образом, относить вещество к проводникам или изоляторам, можно только при учете характерных времен протекающих электрических процессов: если эти времена значительно меньше \(~\tau_3 = \varepsilon_0 \rho\), то вещество можно отнести к диэлектрикам, если же времена процессов значительно больше времени релаксации, то вещество следует считать диэлектриком. Действительно, для быстрых процессов, перемещением зарядов внутри вещества можно пренебречь.

Так, например, если внутри рассмотренного конденсатора находится деревянная дощечка (ρ ≈ 10¹⁰ Ом·м, τ₃ ≈ 0,1 с), то при включении его в цепь переменного тока с частотой порядка 10³ с^-1 (тысяча колебаний в секунду, период колебания одна тысячная секунды) древесину можно считать идеальных диэлектриком. Если этот конденсатор зарядить, то он разрядится через одну десятую долю секунды, то есть через этот промежуток времени древесину можно считать проводником (но, конечно, не идеальным).

Итак, мы рассмотрели некоторые процессы, определяющие времена установления тока и распределения зарядов на проводнике. Сразу оговоримся, что мы рассмотрели не все явления, влияющие на переходные процессы в электрических цепях. Еще одним из важнейших процессов подобного рода является возникновение магнитного поля при протекании электрического тока. С ним познакомимся позднее, при изучении свойств магнитного поля.

Примечания

Следующая страница