Слободянюк А.И. Физика 10/12.6
§12. Постоянное магнитное поле
12.6 Закон Био-Саварра-Лапласа.
Как мы установили, магнитное поле действует с некоторой силой на движущиеся электрические заряды, но оно и создается движущимися зарядами. Сейчас нам предстоит получить основной закон магнитостатики, позволяющий рассчитывать характеристики магнитного поля, создаваемого произвольной конфигурацией постоянных электрических токов – закон Био-Саварра-Лапласа. Этот закон играет в магнитостатике роль аналогичную закону Кулона в электростатике. Однако он с математической точки зрения является более сложным – не случайно его авторами являются трое французских ученых. Подчеркнем, что этот закон не может быть выведен на основании более общих законов, потому, что таковых не существует. Этот закон следует рассматривать как обобщение многочисленных экспериментальных данных. Поэтому мы рассмотрим только некоторые основные обоснования, как экспериментальные, так и общетеоретические.
В данном разделе мы рассмотрим магнитное поле в вакууме, то есть в отсутствии сред, подвергающихся воздействию магнитного поля. Влияния различных веществ на характеристики поля проявляется благодаря возникновению индуцированных токов намагничения (о которых речь пойдет позднее), эти токи создают магнитное поле так же, как и обычные токи проводимости.
В качестве элементарного источника поля мы выберем уже рассмотренный нами элемент тока \(~I \Delta \vec l\) - малый прямолинейный участок тонкого проводника с током. Если ранее такой элемент рассматривался нами как прибор для обнаружения и исследования магнитного поля, сейчас он будет играть роль источника.
Ситуация аналогична той, с которой мы встретились в электростатике – там точечные заряды также выступали в разных ролях: как источник поля и как прибор для изучения самого поля (этот заряд мы называли пробным). Отметим также, что экспериментально можно проверить не сам закон (то есть распределение магнитного поля элемента тока), а только следствия из него – поля создаваемые реализуемыми конфигурациями электрических токов.
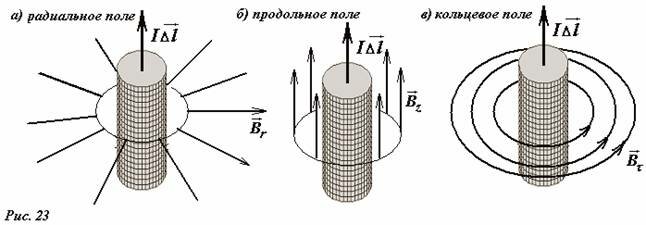
Выбранный [1] источник поля – прямолинейный элемент тока \(~I \Delta \vec l\) обладает осевой симметрией [2] (его свойства не изменяются при повороте на произвольный угол вокруг собственной оси), поэтому и магнитное поле, создаваемое этим элементом должно также обладать той же симметрией. Имеется три принципиально различных конфигурации поля, обладающие требуемой симметрией: осесимметричное радиальное (Рис. 23.а), продольное (Рис. 23.б) и круговое поле (Рис. 23.в).
Конечно, возможна и любая суперпозиция этих полей. Отдать предпочтение одной из этих конфигураций поля на основании только теоретических рассуждений невозможно [3]. Поэтому необходимо обратится к результатам экспериментальных исследований. Эти результаты однозначно показывают, что изучаемое поле является круговым (Рис. 23. в). Простейшее доказательство можно получить с помощью железных опилок, которые в поле прямого проводника с током выстраиваются в вдоль концентрических окружностей, центры которых располагаются на оси проводника.
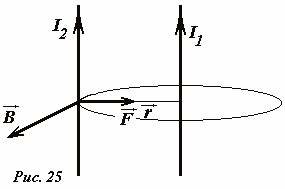
Рассмотрим еще раз один из опытов А.М. Ампера, в котором исследовалось взаимодействие двух длинных параллельных проводников, по которым протекают постоянные электрические токи I1 и I2 (Рис. 25). Оказывается, что в этом случае проводники притягиваются друг к другу, то есть сила, действующая на проводник, направлена вдоль прямой, соединяющей проводник. Легко заметить, что при наличии радиальной составляющей магнитного поля, имелась бы составляющая силы взаимодействия, направленная по касательной окружности с центром на втором проводнике.
Таким образом, силовые линии магнитного поля рассматриваемого элемента тока являются окружностями, то есть силовые линии замкнуты. Так как силовые линии элементарного источника не имеют ни начала, ни конца, то и силовые линии любого магнитного поля обладают тем же свойством – не имеют начала и конца, являются замкнутыми (в исключительных случаях идут из «бесконечности» на «бесконечность»). Это свойство магнитного поля также связано с отсутствием магнитных зарядов.
Отметим также, А.М. Ампер установил, что сила притяжения между проводниками обратно пропорциональна расстоянию между проводниками, этот факт мы используем ниже.
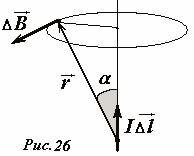
Таким образом, на основании экспериментальных данных мы обязаны заключить, что магнитное поле, создаваемое элементом тока является круговым с осью симметрии, совпадающей с ось элемента тока (Рис. 26), то есть вектор индукции этого поля \(~\Delta \vec B\) в произвольной точке направлен перпендикулярно элементу тока \(~I \Delta \vec l\) и вектору, соединяющему элемент тока с точкой наблюдения \(~\vec r\). Следовательно, направление вектора индукции можно выразить через векторное произведение этих векторов \(~I \Delta \vec l \times \vec r\) .
Разумно предположить, что для магнитного поля справедлив принцип суперпозиции: вектор индукции магнитного поля, создаваемого системой токов, равен сумме векторов индукции полей, создаваемых каждым током в отдельности. Это свойство магнитного поля полностью подтверждается многочисленными экспериментами. Кроме того, как-то не логично признавать принцип суперпозиции для электрического поля, и не принять его для магнитного поля.
Напомним, что математическим выражением принципа суперпозиции является линейная связь между характеристиками источника (в данном случае – элемент тока, характеризуемый его длиной и силой тока \(~I \Delta \vec l\)) и следствием (магнитным полем и его индукцией \(~\Delta \vec B\)). Таким образом, из принципа суперпозиции следует, вектор индукции пропорционален силе тока, порождающего данное поле и длине элемента тока \(~\Delta B \propto I \Delta l\).
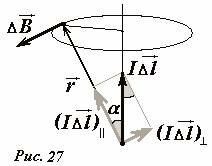
Величина индукции поля может зависеть (и действительно зависит) от направления на точку наблюдения поля, то есть от угла α между вектором элемента тока \(~I \Delta \vec l\) и направлением на точку наблюдения, определяемым вектором \(~\vec r\). Вид этой зависимости можно установить, воспользовавшись принципом суперпозиции и тем опытным фактом, что на оси элемента тока магнитное поле отсутствует. Поэтому разложим вектор элемента тока \(~I \Delta \vec l\) на две составляющие: параллельную \(~(I \Delta \vec l)_{\|}\) , направленную вдоль вектора \(~\vec r\), и перпендикулярную ей \(~(I \Delta \vec l)_{\perp}\) (Рис. 27). Магнитное поле в рассматриваемой точке создается только перпендикулярной компонентой элемента тока, модуль которой равен \(I \Delta l \sin \alpha\) . Следовательно, индукция поля в этой точке пропорциональна синусу угла α между направлением тока и направлением на точку наблюдения.
Наконец, необходимо установить зависимость величины магнитной индукции поля, от расстояния r между источником и точкой наблюдения поля [4]. Конечно, вид этой зависимости может быть установлен только экспериментально. Но почему заранее не предположить, что индукция поля обратно пропорциональна квадрату расстояния до источника \(~B \propto \frac{1}{r^2}\) , как это установлено для гравитационных и электростатических взаимодействий? Эксперимент однозначно подтверждает именно такую зависимость!
Согласно некоторым из современных теорий эта зависимость (закон «обратных квадратов») однозначно связана с трехмерностью пространства, в котором мы живем. При других пространственных зависимостях не выполнялись бы такие замечательные теоремы о потоках и циркуляциях полей.
Объединяя все рассмотренные зависимости в одну формулу, получим, что вектор индукции магнитного поля, создаваемого элементом тока, равен
где K - коэффициент пропорциональности, зависящий от выбора системы единиц измерения. В системе единиц СИ этот коэффициент пропорциональности принято записывать в виде [5]
С множителем \(~\frac{1}{4 \pi}\) в коэффициентах мы знакомы по закону Кулона – он вводится, что бы упростить математические формулы, следующие из этого закона. Величина μ0 называется магнитной постоянной, ее численное значение мы установим чуть позднее, потому что оно связано с определением основной электрической единицы системы СИ - единицей силы тока Ампером.
Заметим, что можно построить систему единиц измерения, в которой данный коэффициент пропорциональности отсутствует (то есть равен безразмерной единице), в этом случае по-другому определяются единицы силы тока, электрического заряда и другие электрические единицы. Такая система единиц (магнитостатическая) была создана и пользовалась определенной популярностью, пока ее не вытеснила международная система СИ.
Окончательно сформулируем основной закон электростатики, названный в честь трех французских ученых, его открывателей – закон Био-Саварра-Лапласа: вектор индукции магнитного поля, создаваемого малым прямолинейным участком проводника с током, пропорционален длине участка проводника, силе тока в нем, синусу угла между элементом тока и направлением на точку наблюдения, обратно пропорционален квадрату расстояния до элемента тока и направлен перпендикулярно плоскости, в которой лежит элемент тока и точка наблюдения в сторону определяемую правилом правого винта (если направление смещения винта совпадает с направлением тока, то направление его вращения совпадает с направлением вектора индукции).
Проще эту формулировку выразить одной формулой
Обратите внимание, что зависимость индукции поля от угла α автоматически выражается в определении векторного произведения (еще раз поразимся удобству этой введенной метаматематической операции). Не смотря, на что в знаменателе этой формулы стоит куб расстояния [6], данная зависимость удовлетворяет закону «обратных квадратов», так как в числителе стоит вектор \(~\vec r\) , и справедливо соотношение \(~|\frac{\vec r}{r^3}| = \frac{1}{r^2}\) .
Запишем (для тех, кто до сих пор не понял, что такое векторное произведение) выражение для модуля вектора магнитной индукции, определяемого формулой (3):
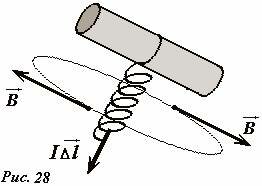
и проиллюстрируем правило правого винта (оно же буравчика и штопора) - Рис. 28.
Интересно подсчитать, сколько пространственных переменных неявно фигурируют в формуле закона Био-Саварра-Лапласа [7]: три координаты, задающие положение элемента, два угла, задающие его направление, три координаты точки, в которой рассчитывается поле – итого 8 (восемь!) пространственных координат. Поэтому при использовании этого закона следует внимательно следить, по каким координатам проводится суммирование – иногда по источникам (при использовании принципа суперпозиции), иногда по точкам наблюдения (при вычислении потока и циркуляции поля), а иногда и то тем и по другим!
Примечания
- ↑ В качестве элементарного источника поля можно было выбрать и другие: например, контур с током, но из таких элементов тяжело конструировать произвольную систему токов; точечный движущийся заряд, но для движущегося заряда законы статики не применимы, так с течением времени его положение изменяется.
- ↑ Точечный источник обладает сферической симметрией, поэтому поле, создаваемое им, обязано быть радиально симметричным
- ↑ Позднее мы покажем, что невозможность радиальной компоненты поля связана с отсутствием в природе магнитных зарядов.
- ↑ Источник поля в данном случае не является точечным, может возникнуть вопрос, до какой точки источника измеряется расстояние. Поэтому следует иметь в виду, что в любом случае подразумевается, что размер элемента тока значительно меньше расстояния до точки наблюдения.
- ↑ Магнитная постоянная оказалась в числителе (в отличие от электрической постоянной в знаменателе закона Кулона), по-видимому, для того, чтобы в магнитостатике все было наоборот: где в электростатике ε0 в числителе, там же в магнитостатике μ0 в знаменателе; если в электростатике что-нибудь «вдоль», то в магнитостатике нечто «поперек», где в электростатике поток, там же в магнитостатике циркуляция и т.д. – в остальном же магнитостатика аналогична электростатике.
- ↑ Сравните с векторной формулой закона Кулона!
- ↑ В законе Кулона их всего шесть: три координаты заряда и три координаты точки наблюдения.