Слободянюк А.И. Физика 10/12.5
§12. Постоянное магнитное поле
12.5 Сила Лоренца.
Магнитное поле действует с некоторой силой на каждую движущуюся заряженную частицу, эта сила называется силой Лоренца (названной в честь голландского физика Генриха Антона Лоренца). Можно считать, что рассмотренная выше сила Ампера является суммой сил Лоренца, действующих на каждую заряженную частицу, направленное движение которых и образует электрический ток.
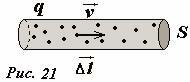
Для того чтобы получить формулу для этой силы представим выражение для элемента тока в виде (рис. 21)
здесь S - площадь поперечного проводника, \(~\vec j = n q \vec \upsilon\) - вектор плотности тока [1], q - электрический заряд движущихся частиц, \(~\vec \upsilon\) - их скорость, n - число частиц в единице объема (концентрация заряженных частиц). Подставим это выражение в формулу для силы Ампера
и заметим, что величина \(n S \Delta l = N\) равна общему числу заряженных частиц в выделенном участке проводника. Поэтому сила, действующая на одну частицу (сила Лоренца) равна
Модуль силы Лоренца рассчитывается по формуле
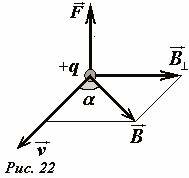
где α - угол между векторами скорости частицы и индукции магнитного поля (Рис. 22). Сила Лоренца направлена перпендикулярно плоскости, в которой лежат векторы скорости частицы \(~\vec \upsilon\) и индукции магнитного поля \(~\vec B\). Направление этой силы можно определить по правилу левой руки, аналогичному правилу для определения направления силы Ампера. Также можно говорить, что на заряженную частицу, действует сила со стороны компоненты поля \(~\vec B_{\perp}\), перпендикулярной вектору скорости. Частица, движущаяся параллельно вектору индукции (то есть вдоль силовой линии магнитного поля), действия силы Лоренца не испытывает. В некоторых учебниках, особенно по теоретической физике, сначала дается формула для силы Лоренца как следствие определения вектора магнитной индукции и обобщения экспериментальных данных, а затем на ее основе выводится выражение для силы Ампера. То, что мы поступили наоборот, несущественно, так обе эти силы имеют одинаковую природу – действие магнитного поля на движущийся заряд.
Примечания
- ↑ Напомним, что за направление силы тока принято направление движения положительно заряженных частиц, поэтому излагаемые здесь правила для определения направления силы Лоренца справедливы для положительных зарядов. Для отрицательно заряженных частиц направление силы Лоренца противоположное.
Смотреть HD
видео онлайн
бесплатно 2022 года