Слободянюк А.И. Физика 10/13.4
§13. Взаимодействие магнитного поля с веществом
13.4 Постоянные магниты.
Постоянные магниты широко используются в различных областях техники и приборостроении: в электроизмерительных приборах, в громкоговорителях, звукозаписывающих устройствах, электродвигателях и др.
Большой популярностью пользуются различные игрушки, принципы действия которых основаны на свойствах магнитов и создаваемых ими магнитных полей.
Все постоянные магниты изготавливаются из магнитно-жестких ферромагнитных материалов, обладающих большим значением остаточной намагниченности.
Оценим возможные значения намагниченности материала и индукции создаваемого им поля.
Сразу оговоримся, что проведенные ниже расчеты носят оценочный характер, так как законы движения частиц в микромире существенно отличаются от законов классической физики. Тем не менее, знакомые нам классические законы все же позволяют оценить порядок возможных значений оцениваемых параметров.
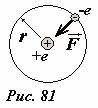
Начнем с оценки возможного значения магнитного момента атома водорода. Будем считать[1], что электрон вращается вокруг ядра по круговой орбите радиуса r (Рис. 81). Этому движущемуся электрону можно поставить в соответствие электрический ток силой
где \(~T = \frac{2 \pi r}{\upsilon}\) - период вращения электрона, υ - его скорость. Тогда магнитный момент этого кругового тока равен
Движущийся электрон обладает также моментом импульса (механическим моментом), равным
где m - масса электрона. Отношение магнитного момента к его механическому моменту
является величиной, не зависящей от параметров орбиты, а зависит только от его заряда и массы. Эта величина играет важную роль во многих процессах, она называется гиромагнитное отношение[2]. Полученное выражение для гиромагнитного отношения остается справедливым и в квантовой физике. Таким образом, для оценки магнитного момента следует найти соответствующий механический момент. Применим второй закон Ньютона для электрона, движущегося по круговой орбите вокруг положительно заряженного ядра: центростремительное ускорение электрона вызывается кулоновской силой его притяжения к ядру
из которого найдем скорость движения электрона
и его момент импульса
Для численной оценки примем диаметр атома равным 1 ангстрему (что близко к экспериментальным значениям), тогда
Полученное значение очень близко к постоянной Планка \(~\hbar = \frac{h}{2 \pi} \approx 1,05 \cdot 10^{-34}\) Дж·с фундаментальной константе, фигурирующей практически во всех формулах квантовой механики. Такое совпадение не является случайным - законы квантовой механики приводят к выводу, что момент импульса, связанный с орбитальным движением электрона составляет величину порядка постоянной Планка. Более того, эта константа служит единицей измерения момента импульса в атомной физике и физике элементарных частиц. Поэтому для дальнейших оценок характерное значение момента импульса атома будем считать равным постоянной Планка \(~L = \hbar\) . Теперь с помощью соотношения (4) выразим магнитный момент атома
Полученная величина является единицей измерения магнитного момента в атомной физике, она называется магнетон Бора \(~\mu_B = \frac{e \hbar}{2 m} \approx 9,27 \cdot 10^{-24} A \cdot m^2\).
В дальнейшем мы будем использовать данное значение в качестве характерной величины магнитного момента атома, хотя для разных атомов их магнитные моменты, конечно, различаются.
Оценим, наконец, максимальное значение намагниченности постоянного магнита. Согласно определению намагниченность равна магнитному моменту единицы объема вещества, поэтому при полном намагничивании, когда магнитные моменты всех атомов ориентированы в одну сторону, намагниченность равна произведению магнитного момента атома на их концентрацию (число атомов в единице объема)
здесь концентрация n выражена через плотность ρ и массу одного атома \(~m_1 = \frac{M}{N_A}\) (M - молярная масса, NA - число Авогадро). Подставляя численные значения для типичного ферромагнетика железа (ρ = 7,9·103 кг/м3, M = 56·10-3 кг/моль), получаем значение намагниченности
Обратите внимание на полученное значение – полная намагниченность приводит к возникновению поверхностного тока намагничивания плотностью порядка восьми тысяч ампер на сантиметр! Такая намагниченность создает магнитная поле индукции B = μ0 J ≈ 1 Тл. Для изготовления постоянных магнитов используются материалы, у которых остаточная намагниченность ненамного меньше намагниченности насыщения. Так в магнитах, изготовленных из прессованного железного порошка, остаточная намагниченность составляет величины порядка Bост ≈ 0,4 - 0,5 Тл , при этом их намагниченность приблизительно равна[3] \(~J = \frac{B}{\mu_0} \approx 4 \cdot 10^5 \frac{A}{m}\) . Интересно отметить, что для того же материала коэрцитивная сила составляет величину порядка 5·10-2 Тл , то есть для размагничивания магнита необходимо поле, индукция которого в сто раз меньше поля самого магнита.
Примечания
- ↑ Еще раз подчеркнем, движение электрона гораздо сложнее – вспомните электронные облака, которые вы рассматривали в курсе химии.
- ↑ Отметим, что для любого равномерно заряженного однородного тела, гиромагнитное отношение определяется формулой (4).
- ↑ Еще раз обратите внимание на полученные значения: когда вы держите небольшой круглый магнит толщиной 1 см, то вы держите в руках кольцевой ток силой в четыре тысячи Ампер.