Слободянюк А.И. Физика 10/17.5
§17. Механические колебания
17.5 Затухающие колебания.
Рассмотренные свободные незатухающие колебания являются идеализацией, моделью применимой на небольших временных интервалах. В реальных механических колебательных системах обязательно присутствуют диссипативные силы (силы трения, силы вязкости), приводящие к уменьшению механической энергии системы из-за ее перехода в другие формы, например, в тепловую. В данном разделе мы рассмотрим описание колебательного движения при наличии таких сил.
17.5.1 Затухание под действием силы сухого трения.
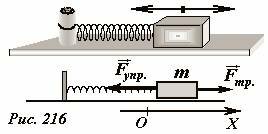
Рассмотрим характер движения пружинного маятника (Рис. 216) с учетом силы сухого трения. Будем считать, что сила, действующая на брусок со стороны горизонтальной поверхности, подчиняется закону Кулона-Амонтона. Коэффициент трения обозначим μ, будем считать, что он не зависит от скорости движения бруска, также пренебрежем различием между трением скольжения и максимальным трением покоя.
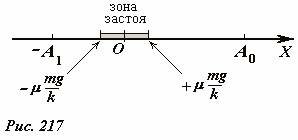
Совмести ось Ox с направлением движения бруска, а ее начало с положением недеформированной пружины. При отклонении бруска на расстояние x, на него в горизонтальном направлении будут действовать силы упругости и сила трения (Рис. 217). Если в этом положении сила упругости \(F_{ynp} = kx\). меньше максимальной силы трения покоя \(F_{mp} = \mu mg\), брусок будет находиться в покое. Таким образом, в интервале, в котором \(k|x| < \mu mg\), или
брусок может находиться в покое, если его скорость равна нулю, поэтому этот интервал является зоной застоя. Пусть начальное отклонение бруска равно A0 лежит вне зоны застоя, начальную скорость будем полагать равной нулю. В этом случае уравнение движения бруска имеет вид (см. рис. 216)
Особо подчеркнем, что это уравнение справедливо только при движении бруска влево, то есть до тех пор, пока скорость бруска отрицательна υ < 0 - при изменении направления движения изменится знак при силе трения[1].
В этом принципиальное отличие этого уравнения от уравнения движения груза, подвешенного на пружине (уравнение (7) из раздела 17.3.1), в котором постоянная сила mg действительно постоянна - не зависит от направления движения. Тем не менее, мы можем воспользоваться рассмотренным ранее методом решения уравнения (2), не забывая об его ограниченной области применимости. Преобразуем уравнение (2) к виду
Это уравнение является уравнением гармонических колебаний для величины \(~x_1(t) = x - \mu \frac{mg}{k}\). Эта функция изменяется по гармоническому закону с частотой, равной частоте свободных колебаний пружинного маятника \(~\omega = \sqrt{\frac{k}{m}}\). Учитывая начальные условия \(x(0) = A_0\), \(\upsilon_0 = 0\), решение уравнения (3) имеет вид
откуда следует закон движения бруска
Скорость бруска будет изменяться по закону
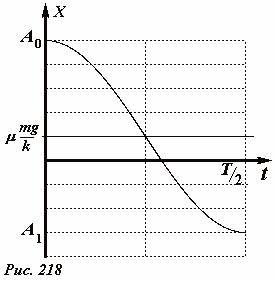
Остановка бруска произойдет в момент времени \(t_1 = \frac{\pi}{\omega} = \frac{T}{2}\) , где T - период свободных колебаний маятника. В момент остановки координата бруска будет равна
Обратите внимание, что координата точки остановки может быть как положительной, так и отрицательной в зависимости от величины начального отклонения. График закона на временном интервале \(~t \le \frac{T}{2}\) показан на Рис. 218 и представляет собой участок косинусоиды, сдвинутый относительно начала отсчета на величину \(~\mu \frac{mg}{k}\). Если точка перовой остановки не попадает в зону застоя, то брусок начнет движение в противоположном направлении. Описание следующей фазы движения аналогично, можно даже полностью воспользоваться полученным решением, для чего достаточно изменить направление оси на противоположное.
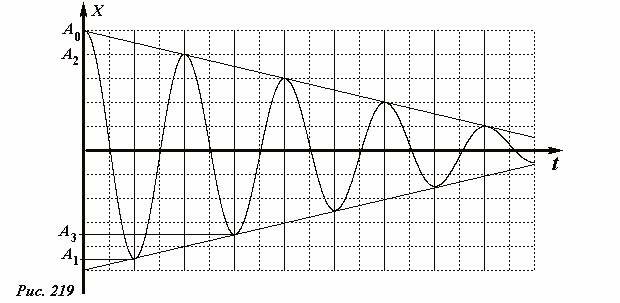
На Рис. 219 показан график закона движения бруска при относительно малом коэффициенте трения, «сшитый» из участков синусоид, аналогичных рассмотренной выше. Между последовательными остановками отклонение бруска уменьшается на постоянную величину
до тех пор пока очередная точка остановки не попадет в область застоя.
Таким образом, постоянная по модулю сила трения не изменяет частоту колебаний, но приводит к уменьшению амплитуды колебаний, причем это уменьшение происходит по линейному закону.
Здесь необходимо сделать одно филологическое замечание. Процесс затухающих колебаний не является периодическим, поэтому использование таких понятий, как период, частота, амплитуда колебаний, строго говоря, не оправдано. Однако при малом затухании эти термины используются: в этом случае под переменной амплитудой колебаний можно понимать отклонение от положения равновесия в моменты остановки, периодом колебаний можно считать промежуток времени между двумя максимальными отклонениями (пусть и различными) в одну сторону. Конечно, при сильном трении (или малом начальном отклонении) движение может содержать только одну фазу: в одну сторону до остановки. Сколько должно быть возвращений два, три..., чтобы движение можно было считать колебательным, решайте самостоятельно.
Рассмотрим теперь превращения различных форм энергии в процессе затухающих колебаний. Начальная энергия пружины \(~U_0 = \frac{kA^2}{2}\), полученная благодаря работе внешней силы при отклонении бруска от положения равновесия, в процессе движения преобразуется в кинетическую энергию движения бруска и частично преобразуется в тепловую энергию из-за наличия трения.
Так при движении бруска от положения начального отклонения \(x = A_0\) до границы зоны застоя \(~x = \mu \frac{mg}{k}\) сила упругости превышает силу трения. На этом участке проходят следующие энергетические процессы:
- - направление смещения совпадает с направлением силы упругости, поэтому сила упругости совершает положительную[2] работу \(\delta A_{ynp} = -kx \Delta x\);
- - потенциальная энергия пружины уменьшается, изменение энергии пружины равно работе силы трения, взятой с противоположным знаком (напомним очевидное: пружина совершает положительную работу, поэтому ее энергия уменьшается) \(\Delta U = -\delta A_{ynp} = kx \Delta x\);
- - сила трения направлена в сторону противоположную направлению перемещения бруска, поэтому ее работа отрицательна \(\delta A_{mp} = \mu mg \Delta x\);
- - количество выделяющейся теплоты равно работе силы трения, взятой с противоположным знаком тр. \(\delta Q = −\delta A\);
- - кинетическая энергия бруска возрастает, причем по теореме о кинетической энергии ее увеличение равно суммарной работе внешних сил, то есть сумме работ сил упругости и силы трения
-
\(~\Delta E_{kin} = \delta A_{ynp} + \delta A_{mp} = -kx \Delta x + \mu mg \Delta x\) . (8) - - в любой момент времени сумма кинетической энергии бруска, потенциальной энергии пружины
и количества выделившейся теплоты равна начальной энергии бруска (что непосредственно следует из уравнения (8)):
-
\(~\frac{m \upsilon^2}{2} + \frac{kx^2}{2} + \mu mg (A_0 - x) = \frac{kA^2_0}{2}\) . (9)
Аналогично можно описать процессы превращения энергии и на других участках движения. Важно не забывать, что всегда работа является мерой перехода энергии из одной формы в другую.
Так с помощью закона сохранения энергии легко получить координату первой точки остановки. Учитывая, что в этой точке скорость и кинетическая энергия бруска равны нулю, запишем уравнение
смысл которого можно выразить словами[3]: сумма потенциальной энергии системы момент остановки и количества выделившейся теплоты равна начальной энергии системы. Из уравнения (10) следует формула (6) для координаты первой остановки.
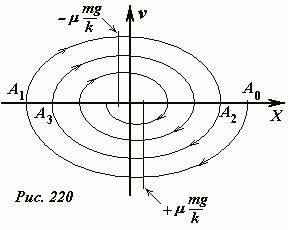
Уравнение закона сохранения энергии (9) позволяет построить фазовую траекторию движения бруска. Путем алгебраических преобразований это уравнение приводится к виду
которое является уравнением эллипса смещенного относительно начала координат. Это уравнение справедливо для первой половины периода колебаний, дальнейшие участки строятся аналогично – результат построения показан на Рис. 220.
17.5.2 Затухание колебаний под действием сил вязкого трения.
Еще одной часто встречающейся причиной затухания колебаний являются силы вязкого трения. Для анализа такого типа движения рассмотрим колебательную систему, показанную на рис. 221. Будем считать, что шарик может двигаться по гладкой горизонтальной поверхности, но в процессе движения на него действует сила сопротивления окружающей среды (например, воздуха). Будем считать, что эта сила пропорциональна скорости движения шарика
Векторная форма записи этого закона, а также отсутствие трения покоя, позволяет рассматривать движение тела во всех его фазах, не зависимо от его направления. Коэффициент пропорциональности в формуле (1) зависит от свойств среды, размеров и формы движущегося тела, в данном разделе мы будем полагать его, как и другие параметры системы известным. Используя традиционные обозначения, запишем уравнение второго закона Ньютона в проекции на горизонтальную ось
Для большей общности незначительно преобразуем этой уравнение, разделив его на массу груза
и введем обозначения появившихся параметров. Величина \(~\frac{k}{m} = \omega^2_0\) есть квадрат круговой частоты свободных колебаний шарика (иногда ее называют собственная частота). Отношение коэффициента сопротивления к массе тела обозначим[4] \(~\frac{\beta}{m} = 2 \gamma\) . В этом случае параметр γ называется коэффициентом затухания. Можно заметить, что этот параметр имеет размерность обратную времени. Следовательно, обратная величина \(\beta^{−1} = \tau\) имеет размерность времени. Далее мы покажем, что она является характерным временем затухания колебаний. С учетом этих обозначений уравнение приобретает вид
|
|
Это уравнение называется уравнением затухающих колебаний. Можно сказать, что изученное нами уравнение свободных колебаний \(a = - \omega^2_0 x\) является частным случаем уравнения (3), в котором коэффициент затухания равен нулю. Поэтому, при малом значении этого коэффициента решение уравнения (3) должно быть похоже на гармонические колебания.
По прежнему, неизвестной величиной уравнения (3) является функция x(t) - зависимость координаты тела от времени. Помимо самой неизвестной функции в уравнение входят ее первая (скорость) и вторая (ускорение) производные. Для однозначного определения закона движение к этому равнению необходимо добавить начальные условия. Будем считать, что в момент времени t = 0 шарик отклонили от положения равновесия на величину \(x(0) = A_0\) и отпустили без толчка \(\upsilon(0) = 0\).
При задании начальных условий уравнение (3) может быть решено однозначно, правда сама процедура поиска решения требует определенной математической подготовки, поэтому в нашем изложении мы ее опустим. В явном виде решение уравнения (3) при заданных начальных условиях и не слишком большой силе вязкости имеет вид[5]
где обозначено
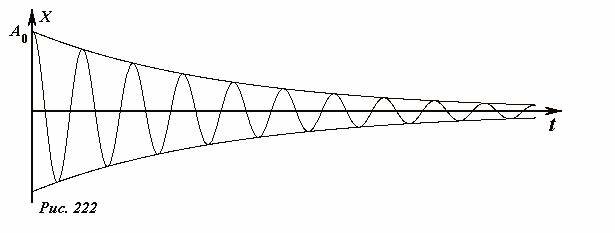
Схематический график этой функции показан на рис. 222.
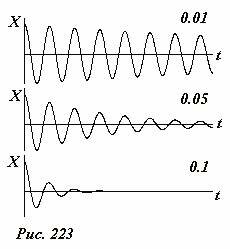
Отметим, наиболее существенные особенности решения уравнения затухающих колебаний (3). Наличие силы вязкого трения приводит к уменьшению амплитуды колебаний. Причем в отличие от рассмотренного затухания под действием силы сухого трения амплитуда убывает нелинейно. Далее мы покажем, что это убывание происходит в геометрической прогрессии. При наличии вязкого трения частота колебаний уменьшается по сравнению с частотой свободных колебаний. Это уменьшение качественно понятно: сила трения замедляет движение, что и приводит к увеличению периода и уменьшению частоты. Если затухание не велико, этим изменением частоты можно пренебречь. Точный вид зависимости частоты от коэффициента затухания дает формула (5). На Рис. 223 показаны несколько графиков решения рассматриваемого уравнения при различных значениях коэффициента затухания. Числа на графиках указывают значение параметра \(~\frac{\gamma}{\omega_0}\).
Отметим, что при γ ≥ ω0 движение тела перестает быть колебательным. В этом случае (сильного затухания) тело монотонно стремится к положению равновесия.
Проанализируем теперь процесс затухания колебаний с энергетической точки зрения. Разобьем область движения тела на малые интервалы Δx. В пределах каждого интервала справедливо уравнение (3), которое мы умножим на величину интервала Δx
Выясним теперь смысл каждого слагаемого этого уравнения. Используя определения ускорения и скорости, преобразуем выражение в левой части
Проведенные преобразования показывают, что эта величина есть изменение кинетической энергии шарика. Первое слагаемое в правой части есть работа сила упругости на малом интервале смещения шарика, и она может быть представлена в виде
Полученные результат очевиден: так как сила упругости потенциальна, то работа этой силы равна уменьшению потенциальной энергии пружины.
Наконец последнее слагаемое является работой силы вязкого трения. Эта сила не является потенциальной, поэтому ее работа не может быть выражена через изменение потенциальной энергии. Работа силы трения, взятая с противоположным знаком, равна количеству теплоты, выделившейся на данном интервале
Таким образом, уравнение (6) в виде
допускает очевидное энергетическое истолкование: уменьшение механической энергии системы равно количеству выделившейся теплоты.
При слабом затухании можно приближенно вычислить потери механической энергии. Для этого применим широко распространенный метод, к помощи которого будем прибегать и далее. Еще раз преобразуем выражение для количества выделяющейся теплоты: с помощью соотношения \(\Delta x = \upsilon \Delta t\) перейдем от изменения координаты к временному интервалу Δt
Видно, что мощность выделяющейся теплоты пропорциональна квадрату скорости \(P = \beta \upsilon^2\). Для того чтобы точно вычислить потери механической энергии (равные выделившейся теплоте) необходимо знать зависимость скорости тела от времени, или закон движения, то есть точно решить уравнение движения. Но в том случае, когда затухание мало, то на небольшом интервале времени можно пренебречь влиянием силы вязкого трения[6]. Продемонстрируем этот подход. Пусть после n колебаний амплитуда отклонения равна An. Пренебрегая вязким трением, запишем закон движения тела (изменением частоты также пренебрегаем):
которому соответствует следующая зависимость скорости тела от времени
Следовательно, мощность выделяющейся теплоты изменяется с течением времени по закону
Теперь легко найти среднюю за период колебания мощность тепловых потерь
= \beta A^2_n \omega^2_0 <\sin^2 \omega_0 t> = \beta A^2_n \omega^2_0 < \frac{1 - \cos 2 \omega_0 t}{2} > = \frac{1}{2} \beta A^2_n \omega^2_0\) . (13)</center>
При выводе последнего соотношения учтено, что среднее значение косинуса за период, очевидно равно нулю.
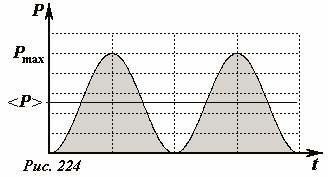
Учитывая, что подобные усреднения нам предстоит неоднократно проделывать в дальнейшем, приведем еще одно наглядное геометрическое доказательство полученного результата. Построим график зависимости мощности от времени \(P = P_{max} \sin^2 \omega_0 t\). Площадь под графиком зависимости тепловой мощности от времени (на рисунке заштрихована) равна количеству выделившейся теплоты. Проведя горизонтальную прямую на уровне половины максимальной мощности, получим прямоугольник, площадь которого равна площади заштрихованной фигуры. Поэтому величина \(~\frac{1}{2} P_{max}\) равна средней мощности.
Таким образом, потери механической энергии за один период колебаний равны
<center>\(~\Delta E = <P>T = \frac{1}{2} \beta A^2_n \omega^2_0 \frac{2 \pi}{\omega_0} = \pi \beta A^2_n \omega_0\) . (14)</center>
Учитывая, что в моменты максимального отклонения скорость шарика обращается в нуль, из уравнения энергетического баланса (10) получим соотношение, описывающее уменьшение амплитуды за одно колебание
<center>\(~\frac{k A^2_n}{2} - \frac{k A^2_{n+1}}{2}= \pi \beta A^2_n \omega_0\) . (15)</center>
Обозначим \(~\frac{k A^2_n}{2} = E_n\) - механическая энергия пружинного маятника после совершения n колебаний. Изменение этой энергии описывается выражением, следующим из (15)
<center>\(~E_n - E_{n+1}= \pi \beta \omega_0 \frac{2 E_n}{k}\) . (16)</center>
Коэффициент в правой части с помощью введенных обозначений преобразуем к виду
<center>\(~\frac{2 \pi \beta \omega_0}{k} = \frac{2 \pi}{\omega_0} \frac{\beta \omega^2_0}{k} = \frac{2 \pi}{\omega_0} \frac{\beta}{k} \frac{k}{m} = \frac{2 \pi}{\omega_0} \frac{\beta}{m} = 2 \gamma T\) ,</center>
с учетом которого перепишем соотношение (16)
<center>\(~E_n - E_{n+1}= 2 \gamma T E_n\) .</center>
Из этого соотношения следует формула
<center>\(~E_{n+1}= (1 - 2 \gamma T) E_n\) ,</center>
указывающая, что механическая энергия убывает в геометрической прогрессии
<center>\(~E_n = E_0(1 - 2 \gamma T)^n\) . (17)</center>
Используя связь между энергией и амплитудой колебаний, получим явное выражение для изменения амплитуды
<center>\(~A_n = A_0 \left( \sqrt{1 - 2 \gamma T} \right )^n \approx A_0 (1 - \gamma T)^n\) , (18)</center>
при выводе которого использована приближенная формула \((1 + \xi)^\alpha \approx 1 + \alpha \xi\) для квадратного корня. Формула (18) показывает, что амплитуда колебания также убывает в геометрической прогрессии. Безразмерная величина γT равна относительному уменьшению амплитуды за один период колебания.
Напомним, что полученные выводы справедливы для малого затухания. Теперь можно дать количественный критерий малости затухания, описываемого уравнением (3): приведенный вывод остается справедливым при выполнении условия
<center>\(~\gamma T = \gamma \frac{2 \pi}{\omega_0} << 1\) . (19)</center>
Примечания
- ↑ Можно записать это уравнение в форме применимой на всех этапах движения, представив силу трения в виде \(F_{mp} = -\mu mg \frac{\upsilon}{|\upsilon|}\), где υ - скорость бруска. В этой записи явно показано, что сила трения направлена в сторону противоположную скорости. Но, во-первых, необходимо анализировать условия начала движения после каждой остановки, во-вторых, все равно его необходимо решать поэтапно, что мы и сделаем.
- ↑ Не удивляйтесь появлению знака минуса в формуле: на этом участке Δx < 0. Кроме того, обращайте внимание на обозначения (букв не хватает!) A0, A1, A2, ... - амплитуды; δA - работа.
- ↑ Это истолкование не единственно, возможна, например, и такая формулировка: уменьшение механической энергии системы равно количеству выделившейся теплоты.
- ↑ Мы уже привыкли к необычным, на первый взгляд, обозначением. Появление в обозначении множителя «2» упрощает проведение дальнейших преобразований.
- ↑ Учитывая, что многие «боятся» показательной функции, в дальнейшем мы эту функцию мы использовать не будем.
- ↑ Звучит парадоксально: чтобы рассчитать затухание следует им пренебречь!