Слободянюк А.И. Физика 10/17.6
§17. Механические колебания
17.6 Вынужденные колебания. Резонанс.
17.6.1 Уравнение вынужденных колебаний и его решение.
Потери механической энергии в любой колебательной системе из-за наличия сил трения неизбежны, поэтому без «подкачки» энергии извне колебания будут затухающими. Существует несколько принципиально различных способов создания колебательных систем незатухающих колебаний. Остановимся более подробно на рассмотрении незатухающих колебаний под действием внешней периодической силы. Такие колебания называются вынужденными.
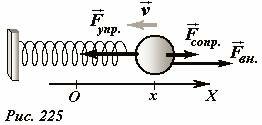
Продолжим изучение движения гармонического маятника (Рис. 225). Помимо рассмотренных ранее сил упругости и вязкого трения, на шарик действует внешняя вынуждающая периодическая сила, изменяющаяся по гармоническому закону
частота, которой может отличаться от собственной частоты колебаний маятника ω0.
Природа этой сил в данном случае нам не существенна. Создать такую силу можно различными способами, например, сообщить шарику электрический заряд и поместить его во внешнее переменное электрическое поле.
Уравнение движения шарика в рассматриваемом случае имеет вид
Разделим его на массу шарика и используем прежние обозначения параметров системы. В результате получим уравнение вынужденных колебаний:
|
|
где \(~f_0 = \frac{F_0}{m}\) - отношение амплитудного значения внешней вынуждающей силы к массе шарика.
Общее решение уравнения (3) достаточно громоздко и, конечно, зависит от начальных условий. Характер движения шарика, описываемого уравнением (3), понятен: под действием вынуждающей силы возникнуть колебания, амплитуда которых будет возрастать. Этот переходный режим достаточно сложен и зависит от начальных условий. По прошествии некоторого промежутка времени колебательный режим установится, их амплитуда перестанет изменяться. Именно установившийся режим колебаний, во многих случаях представляет основной интерес. Мы не будем рассматривать переход системы к установившемуся режиму, а сконцентрируем внимание на описании и изучении характеристик этого режима. При такой постановке задачи нет необходимости задавать начальные условия, так как интересующий нас установившийся режим не зависит от начальных условий, его характеристики полностью определяются самим уравнением.
С аналогичной ситуацией мы сталкивались при изучении движения тела под действием постоянной внешней силы и силы вязкого трения
По прошествии некоторого времени тело движется с постоянной установившейся скоростью \(~\upsilon = \frac{F_0}{\beta}\), которая не зависит от начальных условий, и полностью определяется уравнением движения. Начальные условия определяют режим, переходный к установившемуся движению.
На основании здравого смысла разумно предположить, что в установившемся режиме колебаний шарик будет колебаться с частотой внешней вынуждающей силы. Поэтому решение уравнения (3) следует искать в гармонической функции с частотой[1] вынуждающей силы.
Для начала решим уравнение (3), пренебрегая силой сопротивления
Попробуем[2] найти его решение в виде гармонической функции
Для этого вычислим зависимости скорости и ускорения тела от времени, как производные от закона движения
и подставим их значения в уравнение (4)
Теперь можно сократить на cos ωt. Следовательно, это выражение обращается в верное тождество в любой момент времени, при выполнении условия
Таким образом, наше предположение о решении уравнения (4) в виде (5) оправдалось: установившийся режим колебаний описывается функцией
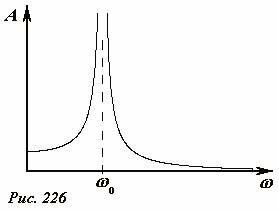
Отметим, что коэффициент A согласно полученному выражению (6) может как положительным (при ω0 < ω), так и отрицательным (при ω0 > ω). Изменение знака соответствует изменению фазы колебаний на π (причина такого изменение будет выяснена чуть позже), поэтому амплитудой колебаний является модуль этого коэффициента A. Амплитуда установившихся колебаний, как и следовало ожидать, пропорциональна величине вынуждающей силы. Кроме того, эта амплитуда сложным образом зависит от частоты вынуждающей силы. Схематический график этой зависимости показан на Рис. 226.
Как следует из формулы (6) и хорошо видно на графике, при приближении частоты вынуждающей силы к собственной частоте системы амплитуда резко возрастает. Причина такого возрастания амплитуды понятна: вынуждающая сила «во время» подталкивает шарик, при полном совпадении частот установившейся режим отсутствует – амплитуда возрастает до бесконечности. Конечно, на практике такого бесконечного возрастания наблюдать невозможно: во-первых, это может привести к разрушению самой колебательной системы, во-вторых, при больших амплитудах колебаний нельзя пренебрегать силами сопротивления среды.
Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте колебаний системы называется явлением резонанса.
Приступим теперь к поиску решения уравнения вынужденных колебаний с учетом силы сопротивления
Естественно, что и в этом случае решение следует искать в виде гармонической функции с частотой вынуждающей силы. Легко заметить, что поиск решения в форме (5) в данном случае не приведет к успеху. Действительно, уравнение (8), в отличие от уравнения (4), содержит скорость частицы, которая описывается функцией синуса. Поэтому, временная часть в уравнении (8) не сократится. Следовательно, решение уравнения (8) следует представить в общей форме гармонической функции
в которой два параметра A0 и φ необходимо найти с помощью уравнения (8). Параметр A0 является амплитудой вынужденных колебаний, φ - сдвиг фаз между изменяющейся координатой и переменной вынуждающей силой. Используя тригонометрическую формулу для косинуса суммы, функцию (9) можно представить в эквивалентной форме
которая также содержит два параметра \(B = A_0 \cos \varphi\) и \(C = -A_0 \sin \varphi\), подлежащих определению. Используя функцию (10), запишем явные выражения для зависимостей скорости и ускорения частицы от времени
и подставим в уравнение (8):
Перепишем это выражение в виде
Для того чтобы равенство (13) выполнялось в любой момент времени необходимо, чтобы коэффициенты при косинусе и синусе были равны нулю. На основании этого условия получаем два линейных уравнения для определения параметров функции (10):
Решение этой системы уравнений имеет вид
На основании формулы (10) определяем характеристики вынужденных колебаний:
амплитуду
сдвиг фаз
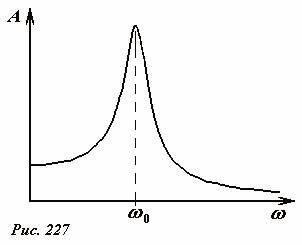
На Рис. 227 показана схематическая зависимость амплитуды вынужденных колебаний A от частоты вынуждающей силы ω. При малом затухании эта зависимость имеет резкий максимум при приближении частоты вынуждающей силы ω к собственной частоте системы ω0. Таким образом, и в этом случае возможно возникновения резонанса, поэтому построенные зависимости часто называют резонансной кривой. Учет слабого затухания показывает, что амплитуда не возрастает до бесконечности, ее максимальное значение зависит от коэффициента затухания – с возрастанием последнего максимальная амплитуда быстро убывает.
Полученная зависимость амплитуды колебаний от частоты вынуждающей силы (16) содержит слишком много независимых параметров (f0, ω0, γ0) для того, чтобы построить полное семейство резонансных кривых. Как и во многих случаях, эту зависимость можно существенно упростить, перейдя к «безразмерным» переменным. Преобразуем формулу (16) к следующему виду
и обозначим \(~\tilde{\omega} = \frac{\omega}{\omega_0}\) - относительная частота (отношение частоты вынуждающей силы к собственной частоте колебаний системы); \(~\tilde{A} = \frac{A}{A_0}\) - относительная амплитуда (отношение амплитуды колебаний к величине отклонения \(~A_0 = \frac{f}{\omega^2_0}\) при нулевой частоте); \(~\delta = \frac{2 \gamma}{\omega_0} = \frac{\gamma T}{\pi}\) - безразмерный параметр[3], определяющий величину затухания. Используя эти обозначения, функция (16) существенно упрощается
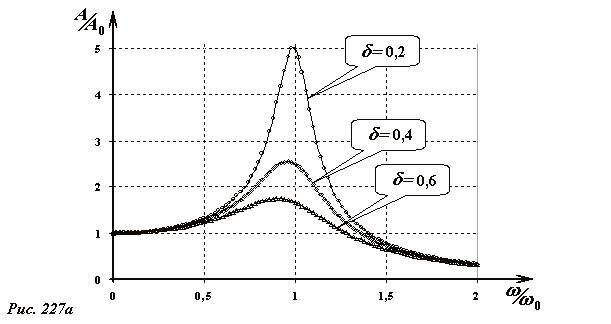
так как содержит всего один параметр - δ. Однопараметрическое семейство резонансных кривых, описываемых функцией (16 б) может быть построено, особенно легко с помощью компьютера. Результат такого построения показан на Рис. 227а. Отметим, что переход к «обычным» единицам измерения может быть проведен элементарным изменением масштаба осей координат.
Следует отметить, что частота вынуждающей силы, при которой амплитуда вынужденных колебаний максимальна, также зависит от коэффициента затухания, слегка убывая с ростом последнего. Наконец, подчеркнем, что увеличение коэффициента затухания приводит к существенному увеличению ширины резонансной кривой.
Возникающий сдвиг фаз между колебаниями точки и вынуждающей силой также зависит от частоты колебаний и коэффициента их затухания. Более подробно с ролью этого сдвига фаз мы познакомимся при рассмотрении преобразования энергии в процессе вынужденных колебаний.
17.6.2 Векторное описание колебаний. Векторное сложение колебаний.
Решение уравнения вынужденных колебаний потребовало от нас достаточно громоздких тригонометрических преобразований. Аналогичные проблемы возникают и при решении других задач, связанных со сложением нескольких тригонометрических функций. Поэтому для упрощения подобных математических выкладок разработан специальный математический метод – метод векторных диаграмм, с которым мы сейчас познакомимся.
Этот метод применяется для нахождения суммы гармонических функций одинаковой частоты вида
Каждая такая функция определяется двумя параметрами[4] A и φ. Сумма произвольного числа слагаемых вида (1) также является гармонической функцией того же вида.
Суммирование функций вида (1) может быть проведено аналитически в самом общем случае:
где амплитуда результирующей функции равна
а ее фаза удовлетворяет условию
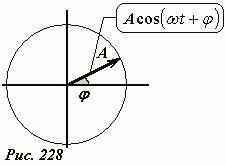
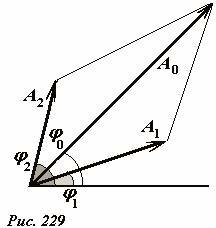
Поведенным преобразованиям можно дать наглядное геометрическое, векторное истолкование. Изучение колебаний мы начали с рассмотрения связи между равномерным вращением вектора и закона движения его проекции. На рис. 228 восстановлена эта связь. Теперь мы скажем, что вектор длиной A, направленный под углом φ к одной из осей может представлять функцию (1). Теперь вместо аналитического сложения функций этого вида можно геометрически сложить векторы, изображающие отдельные слагаемые. При этом важно подчеркнуть, что все функции имеют одинаковые частоты, следовательно, изображающие их векторы вращаются с одной и той же угловой скоростью, поэтому углы между ними не изменяются. Можно сделать следующий шаг – «забыть» об их вращении[5], а складывать неподвижные векторы. Окончательным результатом суммирования будет являться проекция суммарного вектора на исходную ось. Так Рис. 229 иллюстрирует сложение двух гармонических функций с разными амплитудами и разными начальными фазами. Амплитуду A0 и фазу φ0 результирующего колебания можно найти геометрически.
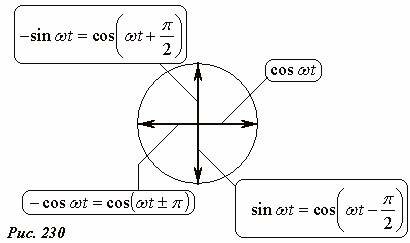
Полезно также запомнить геометрическое представление других тригонометрических функций (Рис. 230). Для этого следует воспользоваться тригонометрическими формулами приведения и «привести» эти функции к виду (1):
Продемонстрируем применение метода векторных диаграмм для решения уравнения вынужденных колебаний.
Зависимости координаты, скорости и ускорения частицы запишем в виде
Подставим эти выражения в уравнение (4), которое запишем в виде
Теперь формально это уравнение имеет следующий смысл: сумма трех гармонических функций с разными амплитудами и фазами равна известной гармонической функции (вынуждающей силе). Изобразим векторную диаграмму суммы трех слагаемых. Пока неизвестное направление оси, от которой отсчитываются углы, можно выбрать произвольно (на рис. 231 она выбрана горизонтально).
Геометрическая сумма этих трех векторов (найти которую в данном случае можно элементарно) должна быть равна вектору, изображающему вынуждающую силу. Так как в исходном уравнении именно эта функция имеет нулевую фазу, то отсчет угла сдвига фаз должен проводится именно от этого вектора. Так на приведенном рисунке этот угол отрицателен, так поворот от вектора, изображающего вынуждающую силу, к вектору, изображающему зависимость x(t), осуществляется в отрицательном направлении («по часовой стрелке»).
Используя построенную диаграмму легко записать уравнение, связывающее амплитуду колебаний и амплитуду вынуждающей силы (на основании теоремы Пифагора):
из которого следует выражение для амплитуды вынужденных колебаний
естественно, совпадающее с полученным ранее аналитическим методом. Векторная диаграмма дает такое же выражение и для сдвига фаз
Таким образом, метод векторных диаграмм позволяет получать точные формулы гораздо быстрее, чем традиционный аналитический метод, основанный на громоздких преобразованиях тригонометрических формул.
17.6.3 Превращения энергии при вынужденных колебаниях.
Внешняя сила, действующая на колебательную систему, совершает работу, следовательно, в систему поступает энергия. Полезно рассмотреть превращения энергии в ходе вынужденных колебаний. Для этого поступим уже традиционным образом:
динамическое уравнение[6] колебаний
умножим на скорость
и перепишем в виде
В этом уравнении каждое слагаемое имеет наглядный физический смысл. Так функция \(P_0(t) = f_0 \cos \omega t \cdot \upsilon(t)\) описывает мгновенную мощность, развиваемой внешней вынуждающей силой. Величина \(2 \gamma \upsilon \cdot \upsilon = f_{sopr}(t) \cdot \upsilon(t) = P_{poteri}(t)\) является мощностью силы сопротивления и описывает потери механической энергии в единицу времени.
Слагаемое \(a(t) \cdot \upsilon(t)\) преобразовывается следующим образом
и равно скорости изменения кинетической энергии колеблющегося тела ΔEkin. Наконец,
есть мощность силы упругости, равная скорости изменения потенциальной энергии системы U. С учетом проведенных преобразований, уравнение (2) приобретает смысл закона сохранения и превращения энергии:
энергия, переданная посредством работы внешней силы, расходуется на увеличение механической энергии системы и работу против сил сопротивления (равную в свою очередь, потерям механической энергии).
Полученное уравнение (3) справедливо для любого промежутка времени, в том числе и на стадии переходного режима. Применим его к режиму установившихся колебаний. В этом режиме колебания являются гармоническими, поэтому за время равное периоду колебаний все характеристики движения (координата, скорость, кинетическая и потенциальная энергия) возвращаются к исходным значениям. Если в уравнении (3) интервал времени Δt положить равным периоду колебаний, то изменение полной энергии будет равно нулю, что приводит к очевидному результату: работа внешней силы за период колебаний равна работе против силы сопротивления. Иными словами, вся энергия, поступающая в систему, превращается в теплоту, выделяющуюся из-за наличия сил сопротивления.
Не составляет труда получить точные значения механической энергии и мощностей всех сил в процессе вынужденных колебаний. Зависимости координаты и скорости от времени нам известны и описываются формулами
В этом режиме полная механическая энергия системы равна
Ее значение колеблется вокруг некоторого среднего значения.
Мощности внешней силы и силы сопротивления описываются формулами
Причем первая принимает как положительные, так и отрицательные значения, а вторая все время положительна.
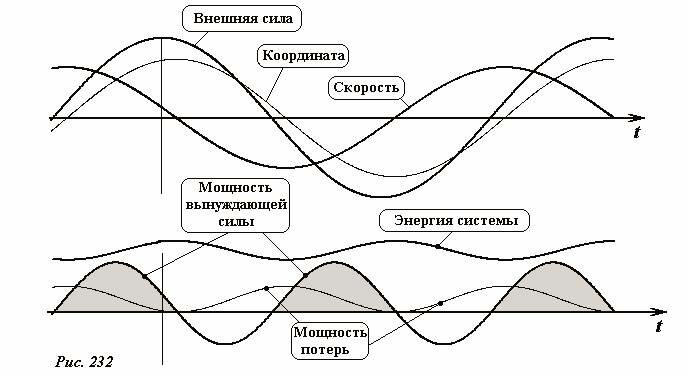
На рисунке 232 показаны графики зависимостей от времени внешней силы, координаты и скорости частицы, ниже построены графики зависимости от времени мощностей внешней силы и силы сопротивления, а также механической энергии. Графики построены для случая, когда частота вынуждающей силы меньше собственной частоты системы ω < ω0, а затухание незначительно. На графиках выделены интервалы времени, когда работа внешней силы положительна, то есть когда энергия поступает в систему.
Эти графики показывают, что мгновенные значения энергетических характеристик даже в установившемся режиме достаточно сложно взаимосвязаны между собой – энергия, сообщаемая внешней силой, расходуется на изменение энергии системы (как кинетической, так и потенциальной), кинетическая энергия переходит в потенциальную и обратно, часть энергии теряется из-за наличия сопротивления.
Более проста ситуация в случае точного резонанса, когда частота вынуждающей силы совпадает с собственной частотой колебаний системы. В этом случае механическая энергия системы остается постоянной, поэтому в любой момент времени мощность внешней силы в точности равна мощности потерь. Сдвиг фаз между вынуждающей силой и координатой точки равен ±π, что приводит к тому, что изменение скорости точки синфазно с изменением внешней силы.
Следует отметить, что рассмотрение мгновенных энергетических характеристик представляет скорее академический интерес, с точки зрения практических применений более важно рассмотрение этих характеристик, усредненных по промежутку времени, значительно превышающему период колебаний. Тем более, это справедливо в тех случаях, когда частота колебаний настолько велика, что различить отдельное колебание не представляется возможным[7].
Проведем расчет усредненных энергетических характеристик в установившемся режиме вынужденных колебаний.
Для начала получим одну важную математическую формулу, которую неоднократно будем использовать в дальнейшем. Пусть две функции изменяются по гармоническому закону с одной и той же частотой
Найдем среднее значение произведения этих функций, используя тригонометрическую формулу для произведения косинусов
Первое слагаемое (косинус разности фаз) не зависит от времени, второе - является переменной функцией времени, очевидно, что ее среднее значение равно нулю. Таким образом, мы получаем, что среднее произведение двух функций равно половине произведения амплитуд, умноженной на косинус сдвига фаз между ними
Частные случаи этой формулы, очевидны, и ранее уже применялись нами. Так при сдвиге фаз равном нулю среднее произведение равно половине произведения амплитуд - ранее мы показали, что среднее значение квадрата косинуса (и синуса) равно 0,5; при сдвиге фаз равном \(~\pm \frac{\pi}{2}\) среднее произведение равно нулю.
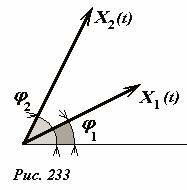
Полученная формула имеет красивую геометрическую интерпретацию на языке векторного представления колебаний. Если гармонические функции представить в векторной форме (в виде вращающихся векторов), то их среднее произведение в соответствии с полученной формулой (8) равно половине скалярного произведения векторов, изображающих функции-сомножители (рис. 233). Обратимся еще раз к рис. 231, на котором построена векторная диаграмма, иллюстрирующая процесс вынужденных колебаний. С ее помощью легко получить те же энергетические характеристики, которые мы нашли аналитически. Убедитесь в этом самостоятельно.
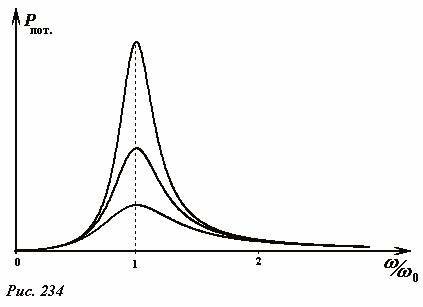
В заключение данного раздела получим явное выражение для средней мощности внешней силы (и равной ей мощности потерь) при вынужденных колебаниях. Эту величину разумно назвать средней мощностью поглощаемой системой. Проще всего это сделать, усредняя мгновенную мощность потерь (6)
при выводе этой функции использовано явное выражение для амплитуды вынужденных колебаний. Схематические графики зависимости поглощенной энергии от частоты вынуждающей силы при различных значениях параметра затухания показаны на рис. 234. Эти графики похожи на зависимости амплитуды от частоты вынуждающей силы (Рис. 227а), но следует помнить, что это, все-таки, разные функции.
Примечания
- ↑ В последовательности нашего изучения колебаний мы все время уходим от частоты собственных колебаний: частота свободных незатухающих колебаний совпадает с собственной частотой, частота затухающих колебаний немного меньше собственной, а частота вынужденных колебаний совпадает с частотой вынуждающей силы, а не собственной частотой.
- ↑ Строгое решение этого уравнения изобилует простыми, но объемными, математическими выкладками, которые затуманивают физический смысл получаемых результатов. Поэтому, мы фактически, будем стараться угадать его решение, основываясь на здравом физическом смысле. Во-первых, такой подход является физическим, а, во-вторых, полученные нами результаты могут быть строго обоснованы математически.
- ↑ Для любителей новых слов укажем, что эта величина называется декрементом затухания и очень часто встречается в теории колебаний.
- ↑ Частоту колебаний ω считаем заданной.
- ↑ Для физиков можно сказать о переходе во вращающуюся систему отсчета.
- ↑ Напомним, что уравнение следует из второго закона Ньютона, которое мы разделили на массу движущегося тела. Слагаемые, стоящие в правой части этого уравнения имеет смысл «удельных» сил, то есть отношений сил к массе тела. Для упрощения изложения в дальнейшем эти слагаемые мы также будем называть «силами»\[-\omega^2_0 x\] - сила упругости, \(2 \gamma \upsilon\) - сила сопротивления, \(+f_0 \cos \omega t\) - вынуждающая сила. Аналогично, энергетические характеристики так же относятся единице массы, поэтому величину \(~\frac{\upsilon^2}{2}\) будем называть кинетической энергией, а величину \(~\frac{\omega^2_0 x^2}{2}\) - потенциальной энергией системы. Кому такие переименования не нравятся, может все выражения этого раздела умножить на массу тела и любоваться знакомыми формулами.
- ↑ Наиболее ярким примером такого положения является изучение взаимодействие света с веществом, где ни один прибор не в состоянии выделить отдельное колебание электромагнитной волны.