Слободянюк А.И. Физика 10/18.10
§18. Переменный электрический ток
18.10 ЛЭП - линия электропередач.
Энергоресурсы распределены на земле неравномерно, поэтому практически постоянно электроэнергия производится в одних местах, а потребляется в других. Поэтому ее приходится передавать и часто на большие расстояния. До сих пор не придумали лучшего способа передачи, чем многокилометровые ЛЭП – проводные линии электропередачи. Не смотря на то, что провода этих линий изготовляют из алюминия, металла с малым удельным электрическим сопротивлением, потери энергии могут быть весьма значительны.
Проведем простейшую оценку. Пусть электроплитка мощностью P = 1кВт, питается от источника напряжением[1] U = 220 В, расположенного на расстоянии l = 1км, линия передачи – из алюминиевого провода радиуса r = 1мм. Найдем потери электроэнергии при ее передаче.
Сопротивление электроплитки найдем из формулы для мощности тока \(P = U^2 R\) :
Сопротивление линии передачи:
(здесь ρ = 2,8·10-8 Ом·м - удельное сопротивление алюминия; не забудьте, что линия состоит из двух проводов). Относительные потери энергии при передаче рассчитаем по формуле
Впечатляющий результат: потери энергии составляют 30%! А если энергию передавать на расстояния в сотни и тысячи километров, да и передаваемые мощности значительно превышают киловатт.
Проведенный расчет показывает, что уменьшение потерь энергии при ее передаче имеет громадное практическое значение.
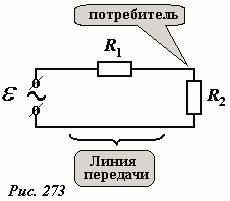
Формализуем данную проблему. Схема простейшей (лучше сказать, примитивной) линии передач показана на рис. 273. Обозначим: R2 - сопротивление нагрузки, R1 - сопротивление линии передачи. В такой цепи коэффициент полезного действия (отношение энергии полученной потребителем к энергии, отданной источником) равно
Можно также ввести коэффициент потерь (отношение энергии, потерянной при передаче, к энергии, отданной источником):
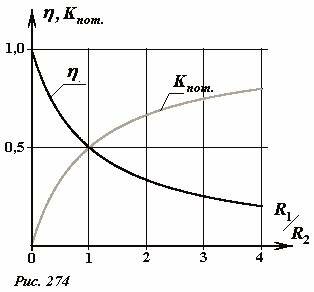
На рис. 274 показаны графики зависимости КПД и коэффициента потерь линии передачи от отношения сопротивлений линии передачи и нагрузки. Отметим, что сопротивление линии передач возрастает при увеличении расстояния (при этом увеличиваются потери). Кроме того, при увеличении мощности нагрузки уменьшается ее сопротивление – что также приводит к увеличению потерь энергии. Поэтому помните – при включении очередного электрического прибора вы увеличиваете потери энергии, не только абсолютные, но и относительные – стоит ли за свой счет напрасно обогревать Вселенную?
Выход из столь печальной ситуации был найден еще на заре электрической эры. Он заключается в увеличении электрического напряжения в линиях электропередач. Увеличение напряжения приводит к уменьшению силы тока и, как следствие, к еще более значительному снижению потерь. Впрочем, мы уже говорили об этом в предыдущем разделе.
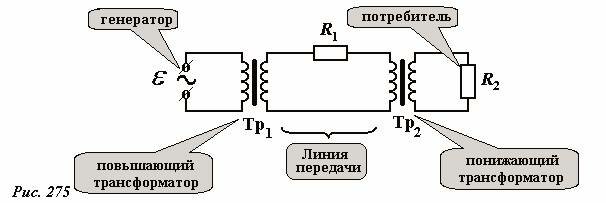
Итак, увеличение напряжения ЛЭП необходимо для уменьшения потерь. С другой стороны, увеличение напряжения в бытовых сетях смертельно опасно для жизни – всегда есть опасность непреднамеренного попадания человека под удар электрическим током. Поэтому напряжение в бытовых сетях не слишком велико[2]: в нашей стране 220 В, в ряде стран – 127 В, используются также 110 В, 240 В. Кроме того, достаточно сложно и опасно создавать электрогенераторы с высоким ЭДС. Таким образом, электроэнергия производится и потребляется при невысоком напряжении, а передаваться должна при высоком. Эти обстоятельства привели к тому, что традиционные линии электропередач строятся по схеме, изображенной на рис. 275.
Наша задача – проанализировать влияние электрического сопротивления линии передачи R1 в такой схеме транспортировки электроэнергии. Для упрощения расчетов мы пренебрежем активным сопротивлением электрогенератора и всего первичного контура – обычно его размеры значительно меньше длины ЛЭП. Также будем считать, что трансформаторы одинаковы, только включены противоположно: во сколько раз повышает напряжение первый, во столько же раз понижает второй. Кроме того, сохраним прежние обозначения для сопротивлений нагрузки и линии передачи.
Методика расчета характеристик этой цепи не отличается от методики расчетов, использованных нами ранее, поэтому здесь наше изложение будет более сжатым. Получим систему уравнений, описывающих характеристики данной цепи, при этом сразу будем строить соответствующие векторные диаграммы, для этих уравнений. Возможность использования метода векторных диаграмм обоснована тем, что генератор создает переменную ЭДС, изменяющуюся по гармоническому закону, поэтому все характеристики (силы токов, напряжения, магнитные потоки, ЭДС индукции) также будут изменяться по гармоническим законам с той же частотой.
Как и ранее, в качестве основы построения векторных диаграмм выберем магнитный поток в сердечнике понижающего трансформатора, зависимость которого от времени запишем в виде
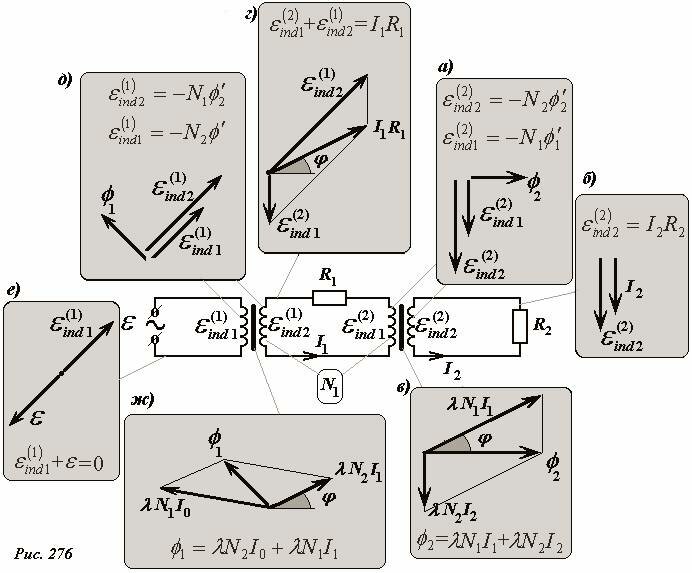
Вектор этого колебания изобразим горизонтальным (Рис. 276а). Изменение магнитного потока индуцирует ЭДС в первичной и вторичной обмотках[3] этого трансформатора, которые в соответствии законом индукции М.Фарадея равны
Соответствующие им векторы колебаний перпендикулярны вектору колебаний магнитного потока, они также изображены на рис. 276а.
ЭДС индукции во вторичной цепи этого трансформатора создает в контуре потребителя электрический ток, сила которого определяется законом Ома
который, в частности утверждает, что вектор колебаний силы тока в этом контуре сонаправлен с вектором индукции (Рис. 276б). Построенные векторы магнитного потока \(~\phi_2\) и силы тока I2, позволяют определить направление вектора колебаний силы тока в линии передачи. Для этого воспользуемся уравнением, определяющим магнитный поток в сердечнике понижающего трансформатора
Это уравнение «изображено» на рис. 276в, угол между векторами силы тока в линии передачи и магнитного потока (т.е. сдвиг фаз между соответствующими колебаниями) обозначен - \(~\phi\). Мы обозначили число витков в первичной обмотке этого трансформатора N1, а во вторичной - N2. Таким образом, коэффициент трансформации равен \(~\kappa = \frac{N_2}{N_1}\). Согласно нашим предварительным рассуждением этот коэффициент должен быть меньше единицы. Будем считать, что столько же витков содержит и повышающий трансформатор, только наоборот: в первичной - N2, во вторичной - N1.
Переходим к контуру линии передач, сила тока в котором подчиняется законом Ома
Уже определенные направления векторов силы тока I1 и ЭДС индукции в первичной обмотке понижающего трансформатора \(\varepsilon^{(2)}_{ind1}\) позволяют построить вектор ЭДС индукции во вторичной обмотке повышающего трансформатора \(\varepsilon^{(1)}_{ind2}\) - рис. 276г. Эта ЭДС создается изменяющимся магнитным потоком в сердечнике повышающего трансформатора \(~\phi_1\). Вектор колебаний этого потока перпендикулярен вектору индукции \(\varepsilon^{(1)}_{ind2}\) (он построен на рис. 276д). Запишем также уравнения закона М.Фарадея, связывающие изменение магнитного потока с ЭДС индукции в обмотках повышающего трансформатора
Как и в любом трансформаторе, векторы колебаний ЭДС индукции в обмотках сонаправлены (Рис.276г). Так как мы пренебрегаем активным сопротивлением в контуре генератора (при необходимости его можно учесть), то уравнение закона Ома для этого контура имеет вид
Следовательно, вектор колебаний ЭДС генератора ε направлен противоположно вектору ЭДС индукции в первичной обмотке повышающего трансформатора (рис. 276е).
Наконец, запишем уравнение для магнитного потока в сердечнике повышающего трансформатора
соответствующая ему векторная диаграмма построена на рис. 276ж.
Подсчитаем[4]: мы записали девять уравнений, содержащих девять неизвестных переменных (два магнитных потока, три силы тока, четыре ЭДС индукции в обмотках).
Таким образом, наша система уравнений является полной и может быть решена. Мы не будем полностью решать данную систему: для анализа потерь электроэнергии в линии передач нам достаточно определить силы токов в цепи потребителя и линии передач, поэтому ограничимся расчетом этих величин. Поэтому стратегия «борьбы с системой уравнений» заключается в скорейшем исключении магнитных потоков и ЭДС индукции в обмотках трансформаторов, выражая их через амплитуды искомых токов и ЭДС генератора.
Начнем с контура генератора: из уравнения (9) выражаем амплитуду ЭДС индукции первичной обмотки повышающего трансформатора
далее из уравнений (8) находим амплитуду ЭДС индукции во вторичной обмотке
Теперь подходим «с другой стороны» - контура потребителя. Из уравнения (5) выражаем амплитуду ЭДС индукции во вторичной обмотке понижающего трансформатора:
а из уравнений (4) Амплитуду ЭДС в первичной обмотке:
Уже можно рассмотреть уравнение для силы тока в контуре линии передачи (7), для амплитуд колебаний величин, фигурирующих в этом уравнении справедливо уравнение (теорема косинусов для соответствующего векторного треугольника на рис. 276г):
В этом уравнении явно «лишним» является синус сдвига фаз, который выразим через амплитуды токов с помощью векторной диаграммы 276в:
Подставим это выражение в уравнение (15), за одно и выражение (14) для ЭДС:
В этом уравнении только две неизвестных величины, причем именно те, которые нас интересуют – амплитуды токов. Нужно еще одно такое же уравнение. Его получим из векторной диаграммы для магнитного потока в сердечнике понижающего трансформатора 276в (теорема Пифагора для векторного треугольника):
К сожалению, в этом уравнении появилась амплитуда магнитного потока, поэтому срочно ее исключаем с помощью уравнения для ЭДС индукции (4):
Подстановка этого выражения в уравнение (18) приводит к требуемому уравнению
Итак, у нас осталось два уравнения (17) и (20) с двумя неизвестными, решение которых не вызывает затруднений. Из (20) выражаем
и подставляем в уравнение(17):
и получаем выражение для амплитуды силы тока в цепи потребителя:
Наконец, с помощью формулы (21) получаем выражение для амплитуды тока в линии передач
Мы достигли поставленной цели, однако полученные выражения[5] достаточно громоздки, поэтому упростим их с помощью разумных (и обоснованных) приближений. Первое: положим, что активное сопротивление нагрузки значительно меньше индуктивного сопротивления вторичной обмотки понижающего трансформатора, то есть пренебрежем слагаемым \(~\left(\frac{R_2}{\lambda N^2_2 \omega}\right) << 1\). Это условие обычно выполняется на практике[6]. Второе: в линиях передач напряжение составляет сотни киловольт, а напряжение в бытовой сети сотни вольт, поэтому введенный коэффициент трансформации \(~\kappa = \frac{N_2}{N_1}\) значительно меньше единицы, поэтому в формуле (22) можно «с чистой совестью» пренебречь квадратичным слагаемым \(~\left(\frac{R_1}{R_2} \frac{N^2_2}{N^2_1}\right)^2\). В рамках этих приближений формулы для токов существенно упрощаются:
Обратите внимание, что в рамках сделанных приближений, сила тока в линии передач в κ раз меньше силы тока в цепи потребителя.
В заключение рассчитаем КПД рассматриваемой линии передачи. Учтем, что сумма мощностей, потребляемой нагрузкой («полезная») и выделяющейся в линии передач («вредная»), равна мощности, развиваемой генератором. Это очевидное утверждение можно доказать и в данном случае. Для этого следует до конца решить полученную систему уравнений и найти силу тока в цепи генератора, но этот раздел и так уже перегружен алгебраическими выкладками, поэтому поверим, что полученные выражения для сил токов верны. Итак, КПД линии передач равен
На последнем шаге мы использовали приближенную формулу, полагая с надеждой, что потери в линии передач не слишком велики. С той же точностью коэффициент потерь равен
Этот результат оправдывает проделанные расчеты: повышение напряжения в линии передач существенно снижает потери. Так, например, повышение напряжения в тысячу раз (реально оно может быть и большим) приводит к уменьшению потерь в миллион раз!
Тот, кто придумал трансформатор, был талантлив! Кстати, этим талантливым изобретателем был американский инженер, серб по национальности, Никола Тесла.
Примечания
- ↑ Напомним, что традиционно указываются действующие значения напряжений и токов.
- ↑ Тяжело обосновать выбор того или иного значения стандарта напряжения в сети – эти значения сложились исторически. Различные значения этого стандарта в разных странах свидетельствуют о том, что не было единого центра развития электроэнергетики, а, может и о неумении и нежелании договариваться. Аналогична ситуация и со стандартом частоты – в Европе принята стандартная частота 50 Гц (полукруглое число), а в Северной Америке – 60 Гц – (наверно, с числом секунд в минуте перепутали).
- ↑ Данная цепь не проста, поэтому приходится усложнять обозначения: все величины, относящиеся к контуру потребителя имеют индекс 2, к контуру линии передачи – индекс 1, к контуру генератора – индекс 0 (при этом все амплитуды будут иметь двойной индекс (второй – 0). Величины ЭДС индукции имеют верхний индекс: (2) – для понижающего трансформатора, (1) - для повышающего. Теоретики утверждают, что удачные обозначения – половина успеха в решении задачи. Кроме того, все обозначения указаны на схеме.
- ↑ Достойно самоуважения! Система из девяти (!) дифференциальных уравнений нас уже не должна очень сильно пугать!
- ↑ Очередной раз обратите внимание на запись формул: сначала самые существенные (и почти очевидные) множители, затем безразмерные коэффициенты, составленные из отношений сопротивлений.
- ↑ Не слишком серьезное обоснование – трансформатор большой, а лампочка над ним маленькая.