Слободянюк А.И. Физика 10/18.9
§18. Переменный электрический ток
18.9 Трансформатор.
18.9.1 Устройство трансформатора.
Широко распространенным устройством для преобразования напряжения в цепях переменного тока является электрический трансформатор, принцип работы которого основан на явлении электромагнитной индукции.
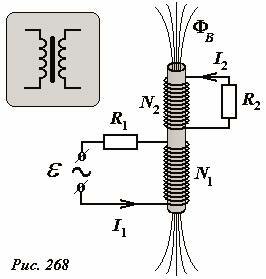
Принципиальная схема трансформатора показана на рис. 268 (в рамке показано его обозначение на электрических схемах). Трансформатор состоит из двух проволочных обмоток (катушек), расположенных на общем сердечнике. Выводы одной из обмоток подключаются к источнику переменной ЭДС, эта обмотка называется первичной. Ко второй обмотке подключаются устройства потребители электрической энергии, эта обмотка называется вторичной. Конечно, разделение обмоток на первичную и вторичную является условным – они могут при необходимости меняться ролями, для нас важно, что источник энергии подключен к первичной обмотке.
Реальные трансформаторы могут содержать несколько вторичных обмоток, так чтобы одновременно получать источники различного напряжения. Часто обмотки трансформатора располагаются одна над одной. Кроме того, сердечники трансформаторов могут иметь различную форму.
Физические принципы работы трансформатора достаточно просты. Переменный электрический ток, создаваемый источником в первичной обмотке создает в сердечнике переменное магнитное поле. Поток этого магнитного поля пересекает и витки вторичной обмотки, поэтому при изменении магнитного потока в ней индуцируется ЭДС индукции, благодаря которой возможно возникновение и поддержание переменного электрического тока в цепи вторичной обмотки.
Отметим, что сердечник является необходимой деталью любого трансформатора. Обычно сердечник изготавливается из ферромагнитных материалов с высокой магнитной проницаемостью, благодаря чему магнитное поле (и его магнитный поток) практически полностью концентрируется внутри сердечника. С этой же целью сердечники трансформаторов, как правило, замкнуты, чтобы магнитный поток не выходил из него. В этом случае потери энергии магнитного поля сводятся к минимуму. Так как магнитное поле в сердечнике является переменным, то в нем также индуцируется электрическое поле, которой может приводить к появлению электрических токов (токов Фуко). Наличие таких токов приводит к разогревы сердечника, и следовательно, к потерям энергии. Во избежание этих потерь сердечники трансформаторов изготовляют из тонких железных пластин, покрытых тонким слоем непроводящих окислов, которые препятствуют возникновению сильных токов. Также во многих случаях сердечники изготовляют из керамических ферромагнетиков (ферритов), электрическое сопротивление которых высоко.
18.9.2 Уравнения, описывающие работу трансформатора.
Рассмотрим математическое описание процессов, протекающих при работе трансформатора. При этом мы будем пользоваться, как обычно, упрощенной математической моделью. Прежде всего, мы будем считать, что магнитный поток, пересекающий все витки как первичной, так и вторичной обмоток трансформатора одинаковым для всех витков. Обозначим это магнитный поток \(~\phi(t)\). Понятно, что он является функцией времени. В этом случае магнитные потоки через первичную и вторичную обмотки[1] выражаются очевидными формулами
где N1, N2 - числа витков в первичной и вторичной обмотках, соответственно.
Обозначим также I1, I2 - силы переменных токов в первичной и вторичных обмотках. Магнитное поле в сердечнике создается электрическими токами в обеих обмотках, поэтому, считая все витки одинаковыми, магнитный поток через один виток может быть записан в виде
В этой формуле λ - постоянный коэффициент, зависящий от формы и размеров витка и магнитной проницаемости сердечника. Согласно этой формуле, магнитный поток, создаваемый током в одном витке равен λI, поэтому величина λ может быть названа индуктивностью одного витка.
В общем случае магнитные потоки через обмотки трансформатора выражаются формулами
в которых постоянные коэффициенты L11, L22 - являются индуктивностями обмоток, а равные коэффициенты L12 = L21 - называются коэффициентами взаимной индукции. В рамках нашей упрощенной модели трансформатора эти коэффициенты выражаются через числа витков
При изменении магнитного потока[2] в обмотках трансформатора возникают ЭДС индукции, которые в соответствии с законом Фарадея равны производным от магнитных потоков
Для упрощения дальнейшего изложения будем считать, что в первичной и вторичной цепях отсутствуют элементы с емкостным и индуктивным (конечно, кроме самих обмоток) сопротивлениями. Активные сопротивления этих цепей обозначим R1, R2, соответственно. В этом случае уравнения закона Ома для первичной и вторичных цепей будут иметь вид
здесь ε - ЭДС источника.
Таким образом, мы получили систему уравнений, описывающих работу трансформатора, включающую:
- - уравнение (3) для магнитного потока в сердечнике (в общем виде уравнения (3а));
- - уравнения (4) для ЭДС индукции в обмотках трансформатора;
- - уравнения закона Ома (5)-(6) для токов в первичном и вторичном контурах (в общем случае они могут включать также и реактивные сопротивления этих контуров).
Эта система из пяти уравнений содержит пять неизвестных функций (\(~\phi(t), \varepsilon_1(t), \varepsilon_2(t), I_1(t), I_2(t)\)) поэтому может быть решена точно. Заметим, что зависимость ЭДС источника от времени является известной функцией, которую мы будем считать изменяющейся по гармоническому закону
Проанализируем полученную систему уравнений. Прежде всего, заметим, что магнитный поток через обмотку пропорционален числу витков в ней, поэтому отношение ЭДС индукции при любом режиме работы трансформатора рано отношению числа витков в обмотках
причем это выражение справедливо как для мгновенных, так и амплитудных значений ЭДС. Отношение числа витков вторичной обмотки к числу витков первичной обмотки \(~\kappa = \frac{N_2}{N_1}\) называется коэффициентом трансформации трансформатора, поэтому отношение ЭДС индукции в обмотках равно коэффициенту трансформации.
Заметим, что если коэффициент трансформации больше единицы, то трансформатор называется повышающим, в противном случае – понижающим.
В практических приложениях более важной характеристикой является отношение напряжения на нагрузке к ЭДС источника, эта величина зависит от характеристик первичного и вторичного контуров.
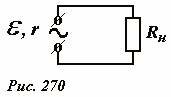
Напомним, что при непосредственном подключении нагрузки к источнику (рис. 270) напряжение на нагрузке меньше ЭДС источника. Действительно по закону Ома сила тока в цепи равна
где Rn - сопротивление нагрузки, r - внутренне сопротивление источника, в это сопротивление также можно включить и сопротивление подводящих проводов (линии передачи). УВ рассматриваемой цепи напряжение на нагрузке равно
что меньше ЭДС источника, и только в том случае когда сопротивление нагрузки значительно превышает сопротивление источника и подводящих проводов \(~\frac{r}{R_n} \to 0\) напряжение на нагрузке стремится к ЭДС источника[3]. Уменьшение напряжения на нагрузке связано с потерями энергии электрического тока в источнике и линии передачи. КПД рассматриваемой цепи (отношение мощности тока через нагрузку к мощности, развиваемой источником) также меньше единицы:
Поэтому уменьшение влияния внутреннего сопротивления источника и линии передачи является важной проблемой, связанной с экономий электроэнергии. Далее мы покажем, что использование трансформаторов позволяет частично решить данную проблему.
18.9.3 «Режим холостого хода»
Вернемся к анализу системы уравнений, описывающих работу трансформатора. Наиболее простым частным случаем является, так называемый «режим холостого хода». Этот режим реализуется, если сила тока во вторичной цепи значительно меньше тока первичной цепи I2 << I1. В этом случае можно пренебречь магнитным потоком, создаваемым током во вторичной цепи. В этом случае напряжение на нагрузке равно ЭДС индукции во вторичной обмотке U2 = εind2. Если также пренебречь активным сопротивлением первичной цепи, то из уравнения (5) следует, что ЭДС индукции в первичной обмотке равно ЭДС источника, взятой с противоположным знаком εind1 = −ε. Поэтому напряжение на первичной обмотке[4], взятое с обратным знаком будет равно ЭДС индукции в этой обмотке U1 = -εind1 и равно ЭДС источника. Следовательно, в этом случае отношение амплитуд напряжений на обмотках (или отношения напряжения на нагрузке к ЭДС источнику) будет равно отношению числа витков
то есть, в режиме холостого хода отношение напряжения на нагрузке к ЭДС источника равно коэффициенту трансформации трансформатора, или напряжение на нагрузке в κ раз превышает ЭДС источника.
Найдем силу тока в первичной цепи. Для этого, используя уравнение (3) для магнитного потока \(~\phi = \lambda N_1 I_1\), запишем уравнение для ЭДС индукции в первичной цепи
С учетом связи ЭДС индукции и ЭДС источника εind1 = −ε и, представляя последнее в виде \(~\varepsilon = \varepsilon_0 \cos \omega t\), получим уравнения для определения силы тока
решение которого имеет вид
Мы получили очевидный результат – выражение для силы тока в цепи, содержащей катушку индуктивности (так как индуктивность первичной обмотки равна \(L = \lambda N^2_1\)). Сдвиг фаз между силой тока и ЭДС источника равен \(~\frac{\pi}{2}\), поэтому средняя мощность тока равна нулю, что очевидно, так как в рассматриваемом приближении ток через нагрузку отсутствует.
Иными словами, при стремлении сопротивления нагрузки к бесконечности КПД цепи стремится к единице, правда, полезная мощность при этом стремится к нулю.
18.9.4 Режим «без потерь».
Рассчитаем теперь характеристики цепи, пренебрегая активным сопротивлением первичной цепи (то есть, пренебрегая внутренним сопротивлением источника, активным сопротивлением первичной обмотки и подводящих проводов). В этом случае отсутствую потери энергии электрического тока, то есть вся энергия источника тока используется потребителем, то есть выделяется на нагрузке.
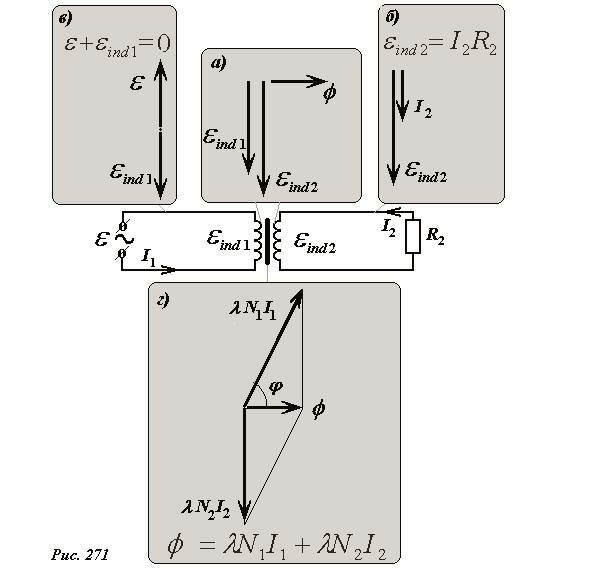
Полученную ранее систему уравнений можно, конечно, решит аналитически. Однако, если ЭДС источника изменяется по гармоническому закону с круговой частотой ω, то все характеристики цепи (токи, напряжения, ЭДС индукции) будут изменяться также по гармоническим законам с той же частотой. Поэтому для решения системы уравнений удобнее воспользоваться методом векторных диаграмм (Рис. 271).
Построение этих диаграмм удобно начать с вектора колебаний магнитного потока в сердечнике трансформатора, так как он является общим для обеих обмоток. Представим зависимость этого потока от времени в виде
как обычно, выбор фазы начальной колебания является произвольным, поэтому здесь мы полагаем его равным нулю, амплитудное значение магнитного потока обозначено \(~\phi_0\) и подлежит определению. Вектор колебания этой величины в соответствии с принятыми нами правилами изобразим горизонтально (Рис. 271а). Производная этого потока по времени задается функцией
следовательно, ЭДС индукции в первичной и вторичной обмотках в соответствии с формулами (4) описываются выражениями
Векторы колебаний этих величин перпендикулярны вектору колебаний магнитного потока, так как их фаза сдвинута на \(~\frac{\pi}{2}\) относительно фазы колебаний магнитного потока. Они также изображены на диаграмме 271а. Амплитудные значения ЭДС выражаются через амплитуду магнитного потока
Далее построим векторную диаграмму для уравнения (6), описывающего ток во вторичной цепи. В соответствии с этим уравнением вектор колебаний силы тока совпадает с направлением вектора индукции (Рис. 271б). Это же уравнение, записанное для амплитудных значений, имеет вид
Уравнение закона Ома для первичной цепи (5) в рассматриваемом приближении R1 = 0 приобретает простой вид
Соответствующая ему диаграмма изображена на рис. 271в. Это уравнение утверждает равенство амплитуд ЭДС источника и индукции первичной обмотки
Наконец, строим векторную диаграмму для уравнения (3), описывающего магнитный поток в сердечнике (Рис. 271г). Здесь вектор величины \(\lambda N_1 I_1\) (это магнитный поток, создаваемый током в первичной обмотке трансформатора) направлен так, чтобы его сумма с вектором \(\lambda N_2 I_2\) совпадала с вектором колебаний магнитного потока \(~\phi\). Угол между этими векторами φ заранее не известен и подлежит определению.
Для решения[5] полученной системы выразим из уравнений (21) и (17) амплитуду магнитного потока
Теперь из уравнения (19) легко определить амплитуду тока во вторичной цепи
Из построенных векторных диаграмм следует, что колебания тока во вторичной цепи проходят в противофазе с колебаниями ЭДС источника.
Напряжение на нагрузке определяется формулой
то есть, отношение этого напряжения к ЭДС источника равно и в этом случае коэффициенту трансформации трансформатора \(~\kappa = \frac{N_2}{N_1}\).
Таким образом, если активное сопротивление первичной цепи пренебрежимо мало, то напряжение на нагрузке в κ раз превышает ЭДС источника. Следовательно, трансформатор можно использовать как для повышения, так и для понижения напряжения на нагрузке.
Для определения силы тока в первичной цепи следует воспользоваться уравнением (3) для магнитного потока. Теорема Пифагора для векторов диаграммы 271г позволяет записать соотношение
из которого следует
Можно отметить, что если разомкнуть вторичную цепь (например, положив R2 → ∞), то формула (27) приводит к очевидному полученному ранее результату
Сдвиг фаз между силой тока в первичной цепи и ЭДС источника, как следует из диаграмм 271в и 271г равен \(~\left(\frac{\pi}{2} - \varphi \right)\) , где угол φ легко определить из последней диаграммы. Так, например, можно записать
Наконец, рассчитаем среднюю мощность, развиваемую источником в данной цепи
(при выводе которого использована формула (24) для амплитуды силы тока во вторичной цепи). Полученное соотношение очевидно[6] – мощность, развиваемая источником, равна мощности, выделяющейся на нагрузке.
18.9.5 Учет потерь.
Учет активного сопротивления первичной цепи принципиально не изменяет физических принципов описания рассматриваемых процессов, однако усложняет математические расчеты.
Единственное изменение, которое необходимо внести в полученную ранее систему уравнений для амплитуд , заключается в замене уравнения (20), полным уравнением для силы тока в первичной цепи
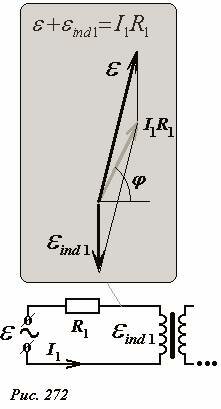
векторная диаграмма для которого изображена на рис. 272. Направление вектора колебаний силы тока I1, по-прежнему определяется уравнением для магнитного потока в сердечнике, поэтому его направление задается предыдущими диаграммами. Вектор колебаний ЭДС источника должен быть направлен так, чтобы его сумма с вектором колебаний ЭДС индукции в первичной цепи была направлена вдоль вектора колебаний силы тока.
Используя теорему косинусов для векторного треугольника, образованного векторами колебаний εind1, ε, I1, R1 можно записать уравнение
В данном уравнении неизвестной также является величина индукции в первичной обмотке εind1 (модуль которой в данном случае отличен от модуля ЭДС источника). Поэтому предпочтительнее выразить все неизвестные величины через амплитуду магнитного потока \(~\phi_0\). ЭДС индукции выражается уравнением (17) \(~\varepsilon_{ind10} = N_1 \phi_0 \omega\), а из диаграммы 271г следует, что
при выводе этого соотношения использовано выражение (18) для ЭДС индукции вторичной обмотки. После подстановки в уравнение (31), получим
откуда следует, что
Наконец, искомые значения сил токов в первичной и вторичной обмотках описываются формулами
Обратите внимание на запись полученных выражений – первые множители в этих выражениях совпадают с полученными ранее выражениями (27) и (24), а последние множители представляют собой безразмерные коэффициенты, в них фигурируют только отношения: чисел витков, сопротивлений, отношений активных и реактивных сопротивлений. Такая форма записи делает наглядным анализ формул. Так сразу видно, что при R1 → 0 эти формулы приводят к выражениям, полученным в приближении «без потерь».
Во многих случаях индуктивное сопротивление первичной цепи значительно превышает ее активное сопротивление, поэтому их отношением \(~\frac{R_1}{N^2_1 \lambda \omega}\) можно пренебречь. В этом приближении напряжение на нагрузке определяется формулой
здесь, по-прежнему, \(~\kappa = \frac{N_2}{N_1}\) - коэффициент трансформации.
Таким образом, активное сопротивление уменьшает напряжение на нагрузке, причем его влияние тем больше, чем больше коэффициент трансформации. Физическая причина этого такого влияния понятна – чем больше коэффициент трансформации, тем больше сила тока в первичной цепи, тем больше падение напряжения на сопротивлении первичной цепи, тем больше потери энергии электрического тока на этом сопротивлении.
Сравнивая полученную формулу с выражением (10) для напряжения на нагрузке в цепи без трансформатора, видим, что, формально, трансформатор изменяет напряжение в κ раз, при этом активное сопротивление изменяется в κ2 раз. Следовательно, для уменьшения потерь выгодно передавать энергию при высоком напряжении, а использовать ее при пониженном, в этом случае κ < 1, поэтому потери снижаются. Данный вывод может быть истолкован «на пальцах»: при увеличении напряжения в линии передач в n раз, во столько же раз снижается сила тока (при постоянной мощности), поэтому потери пропорциональные квадрату силы тока снижаются в n2 раз.
Примечания
- ↑ Напомним, что часто эти величины называют потокосцеплением, однако этот термин далее мы использовать не будем.
- ↑ Конечно, причиной изменения магнитного потока является изменение токов в обмотках, но сами эти токи существенно зависят от ЭДС индукции, поэтому, в очередной раз, разрешить проблему «первичности курицы или яйца» разрешить не удается.
- ↑ Часто ЭДС источника, не совсем верно, ассоциируется с напряжением (вспомните надписи на батарейках). Кроме того, отметим, что данные результаты справедливы для цепей как постоянного, так и переменного тока.
- ↑ Напомним, напряжение на индуктивном сопротивлении предназначено для преодоления ЭДС самоиндукции.
- ↑ Эту систему можно решать различными способами – как вам больше нравится.
- ↑ Оно подтверждает не столько закон сохранения энергии, сколько правильность проделанных расчетов.