Слободянюк А.И. Физика 10/18.8
§18. Переменный электрический ток
18.8 Колебательный контур.
18.8.1 Свободные колебания в контуре.
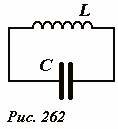
Рассмотренные в предыдущих разделах цепи переменного тока наводят на мысль, что пара элементов – конденсатор и катушка индуктивности образуют своеобразную колебательную систему. Сейчас мы покажем, что это действительно так, в цепи состоящей только из этих элементов (рис. 262) возможны даже свободные колебания, то есть без внешнего источника ЭДС. Поэтому цепь (или часть другой цепи), состоящая из конденсатора и катушки индуктивности называется колебательным контуром.
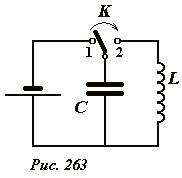
Пусть конденсатор зарядили до заряда q0 и затем подключили к нему катушку индуктивности. Такую процедуру легко осуществить с помощью цепи, схема которой показана на рис. 263: сначала ключ К замыкают в положении 1, при этом конденсатор заряжается до напряжения, равного ЭДС источника, после чего ключ перебрасывают в положения 2, после чего начинается разрядка конденсатора через катушку.
Для определения зависимости заряда конденсатора от времени q(t) применим закон Ома, согласно которому напряжение на конденсаторе \(~U_C = \frac{q}{C}\) равно ЭДС самоиндукции, возникающей в катушке \(~\varepsilon_{si} = -L \frac{\Delta I}{\Delta t} = LI'\) (здесь, «штрих» означает производную по времени). Таким образом, оказывается справедливым уравнение
В этом уравнении содержится две неизвестных функции – зависимости от времени заряда q(t) и силы тока I(t), поэтому его решить нельзя. Однако сила тока является производной от заряда конденсатора q′(t) = I(t), поэтому производная от силы тока является второй производной от заряда
С учетом этого соотношения, перепишем уравнение (1) в виде
Поразительно, но это уравнение полностью совпадает с хорошо изученным нами уравнением гармонических колебаний (вторая производная от неизвестной функции пропорциональна самой этой функции с отрицательным коэффициентом пропорциональности \(x'' = -\omega^2_0 x\))! Следовательно, решением этого уравнения будет гармоническая функция
с круговой частотой
Эта формула определяет собственную частоту колебательного контура. Соответственно период колебаний заряда конденсатора (и силы тока в контуре) равен
Полученное выражение для периода колебаний называется формулой Дж. Томпсона.
Как обычно, для определения произвольных параметров A, φ в общем решении (4) необходимо задать начальные условия – заряд и силу тока в начальный момент времени. В частности, для рассмотренного примера цепи рис. 263, начальные условия имеют вид: при t = 0 q = q0, I = 0, поэтому зависимость заряда конденсатора от времени будет описываться функцией
а сила тока изменяется со временем по закону
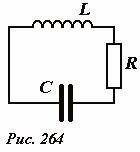
Следует отметить, что приведенное рассмотрение колебательного контура является приближенным – любой реальный контур обладает активным сопротивлением (соединительных проводов и обмотки катушки). Поэтому в уравнении (1) следует учесть падение напряжения на этом активном сопротивлении, поэтому это уравнение приобретет вид
который с учетом связи между зарядом и силой тока, преобразуется к форме
Это уравнение нам также знакомо – это уравнение затухающих колебаний \(x'' = -\omega^2_0 x - \beta x'\), причем коэффициент затухания, как и следовало ожидать, пропорционален активному сопротивлению цепи \(~\beta = \frac{R}{L}\).
Процессы, происходящие в колебательном контуре, могут быть также описаны и с помощью закона сохранения энергии. Если пренебречь активным сопротивлением контура, то сумма энергий электрического поля конденсатора и магнитного поля катушки остается постоянной, что выражается уравнением
которое также является уравнением гармонических колебаний с частотой, определяемой формулой (5). По свое форме это уравнение также совпадает уравнениями, следующими из закона сохранения энергии при механических колебаниях. Так как, уравнения, описывающие колебания электрического заряда конденсатора, аналогичны уравнениям, описывающим механические колебания, то можно провести аналогию между процессами, протекающими в колебательном контуре, и процессами в любой механической системе.
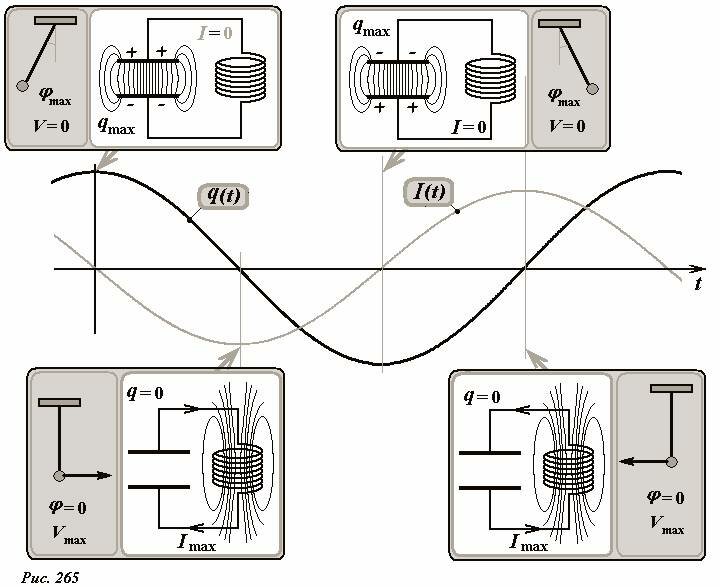
На рис. 265 такая аналогия проведена для колебаний математического маятника. В этом случае аналогами являются «заряд конденсатора q(t) – угол отклонения маятника φ(t)» и «сила тока I(t) = q′(t) – скорость движения маятника V(t)».
Пользуясь этой аналогией, качественно опишем процесс колебаний заряда и электрического тока в контуре. В начальный момент времени конденсатор заряжен, сила электрического тока равна нулю, вся энергия заключена в энергии электрического поля конденсатора (что аналогично максимальному отклонения маятника от положения равновесия). Затем конденсатор начинает разряжаться, сила тока возрастает, при этом в катушке возникает ЭДС самоиндукции, которая препятствует возрастанию тока; энергия конденсатора уменьшается, переходя в энергию магнитного поля катушки (аналогия – маятник движется к нижней точки с возрастанием скорости движения). Когда заряд на конденсаторе становится равным нулю, сила тока достигает максимального значения, при этом вся энергия превращается в энергию магнитного поля (маятник достиг нижней точки, скорость его максимальна). Затем магнитное поле начинает убывать, при этом ЭДС самоиндукции поддерживает ток в прежнем направлении, при этом конденсатор начинает заряжаться, причем знаки зарядов на обкладках конденсатора противоположны начальному распределению (аналог – маятник движется к противоположному начальному максимальному отклонению). Затем ток в цепи прекращается, при этом заряд конденсатора становится опять максимальным, но противоположным по знаку (маятник достиг максимального отклонения), после чего процесс повторятся в противоположном направлении.
18.8.2 Вынужденные колебания в контуре.
Как уже было сказано, в реальном колебательном контуре колебания будут затухающими[1] из-за неизбежного выделения теплоты на активном сопротивлении (которым мы пренебрегли). Поэтому для поддержания незатухающих колебаний в контуре необходим внешний источник энергии, иными словами нам необходимо рассмотреть вынужденные колебания. Один из возможных вариантов осуществления таких колебаний мы уже рассмотрели при изучении темы «Резонанс напряжений», где мы фактически изучили колебания в контуре, внутрь которого включен источник переменной ЭДС, который может считаться аналогом внешней вынуждающей силы.
Чтобы явным образом показать, что явление резонанса напряжений можно рассматривать как вынужденные колебания, перепишем использованное уравнение закона Ома
Для чего подставим в него явные выражения для напряжений на элементах цепи \(~U_C = \frac{q}{C}\) , \(~U_R = IR = Rq'\) , \(~U_L = -\varepsilon_{si} = LI' = Lq''\) и ЭДС источника \(\varepsilon = U_0 \cos \omega t\):
и перепишем его в виде
который полностью совпадает с уравнением вынужденных колебаний \(x'' = -\omega^2_0 x - \beta x' + f_0 \cos \omega t\).
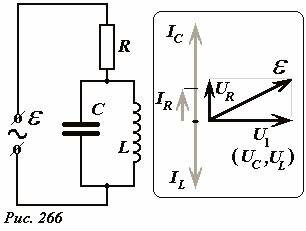
Рассмотрим теперь возможность возникновения вынужденных колебаний в контуре, когда источник переменной ЭДС находится вне контура[2], как показано на рис. 266. Расчет данной цепи проведем, используя метод векторных диаграмм (которая также представлена на рис. 266). В данном случае нас, прежде всего, будет интересовать сила тока в колебательном контуре.
Так как конденсатор и катушка индуктивности соединены параллельно, то мгновенные напряжения (UC, UL) на этих элементах одинаковы. Обозначим это напряжение U1. Построение диаграммы следует начинать с построения вектора, изображающего колебания этого напряжения. Далее построим векторы, изображающие колебания сил токов через конденсатор IC и катушку индуктивности IL - эти векторы перпендикулярны вектору напряжения U1 и противоположны друг другу. Как обычно, колебания токов через конденсатор и через катушку индуктивности происходят в противофазе. Колебательный контур соединен последовательно с резистором, поэтому сумма токов IC и IL (конечно, их мгновенных значений) равна силе тока через резистор IR. Вектор изображающий напряжение на резисторе UR, сонаправлен с вектором суммарного тока. Наконец сумма векторов напряжения на резисторе UR и напряжения на контуре U1 равна ЭДС источника.
Построенная векторная диаграмма позволяет рассчитать амплитудные значения токов и напряжений на элементах данной цепи. Выразим традиционным образом амплитудные значения сил токов через конденсатор и катушку через амплитуду напряжения на контуре
Амплитуда силы тока через резистор (и через источник) определяется из векторной диаграммы и равна
Теперь можно записать выражение для амплитуды напряжения на резисторе
Далее, глядя на диаграмму напряжений, запишем теорему Пифагора для вектора ЭДС источника ⎟ ⎟
здесь U0 - амплитуда ЭДС источника.
Из этого уравнения легко определить напряжение на резисторе
Наконец, с помощью формул (1), (2), (3), запишем выражения для сил токов в рассматриваемой цепи
Проанализируем зависимость этих величин от частоты источника ЭДС. Во всех формулах под корнем имеется два положительных слагаемых, причем только второе зависит от частоты. При частоте
равной собственной частоте колебательного контура второе слагаемое под корнем обращается в ноль, поэтому можно ожидать, что вблизи этой частоты силы токов через конденсатор и катушку достигают максимального значения. Понятно, что максимумы функций IL0(ω) и IC0(ω) несколько смещены от частоты ω0, потому, что частота источника ω присутствует и вне корня. Однако, если первое слагаемое под корнем (\(\frac{1}{R^2}\)), мало, то сдвиг максимума от значения ω = ω0 будет незначительным. Отметим, также, что при \(~\omega = \omega_0 = \frac{1}{\sqrt{LC}}\) амплитуды токов через конденсатор и катушку оказываются равными. Действительно, в этом случае
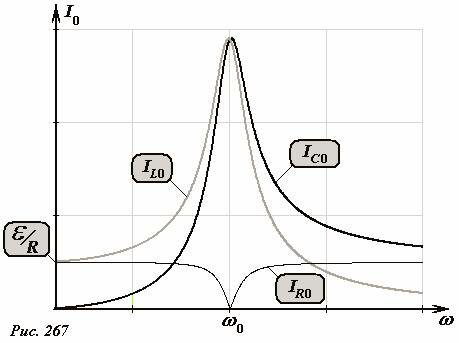
Но самое неожиданное, что при ω = ω0 сила тока через резистор обращается в нуль! Соответственно, напряжение на колебательном контуре становится равным ЭДС источника, что также следует и из полученных формул для токов в контуре. Схематические графики зависимостей[3] амплитуд токов от частоты источника показаны на рис.267. Понятно, что при ω → 0 и ω → ∞ сопротивление контура стремится к нуля и в этом случае сила тока через резистор стремится к своему предельному значению \(~I_{R0} = \frac{U_0}{R}\).
Таким образом, мы показали, что в рассмотренной цепи при частоте источника стремящейся к собственной частоте контура амплитуда силы тока в контуре резко возрастает, наблюдается явление резонанса, следовательно, колебательный контур можно использовать для выделения колебаний требуемой частоты. Интересно, отметить, что острота пика возрастает с ростом сопротивления резистора, находящегося вне контура.
В заключение данного раздела, обсудим, почему при ω = ω0 сила тока во внешней для контура цепи обращается в нуль. Колебания токов через конденсатор IC и через катушку индуктивности происходят в противофазе IL, а в случае ω = ω0 амплитуды этих токов сравниваются, в результате чего формально и получается нулевое значение для суммарного тока. Фактически в этом случае электрический ток циркулирует в колебательном контуре, не выходя из него. Подчеркнем, что наш анализ проведен для установившегося режима колебаний – в переходном режиме ток через резистор (и через источник идет) обеспечивая контур энергией. Когда колебания установятся, подкачка энергии становится излишней, так как мы пренебрегли потерями энергии в контуре. Обратите внимание, что при ω = ω0 сила тока в контуре не зависит сопротивления внешнего резистора, а полностью определяется параметрами контура.
Вспомните, что вынужденные колебания механических систем обладают тем же свойством – при точном резонансе и при отсутствии сил сопротивления работа внешней силы также обращается в нуль.
Если же рассмотреть реальный контур, обладающий активным сопротивлением, то между током в контуре и напряжением на нем разность фаз будет отлична от нуля, поэтому энергия источника будет поступать в контур, компенсируя потери. В этом случае также будет отличен от нуля и ток во внешней цепи.
Примечания
- ↑ Еще одной причиной затухания тока в контуре является излучение электромагнитных волн, но об этом важнейшем явлении мы будем говорить позднее. Сейчас же отметим, что при не слишком высоких частотах, потери энергии на излучения пренебрежимо малы.
- ↑ Опять забегая вперед, скажем, что именно такая схема реализуется в приемниках электромагнитных волн, как радио, так и телевизионных. В этих приборах колебательный контур служит избирательным элементом, выделяющим требуемую волну из широкого спектра. Роль источника в этом случае играет антенна.
- ↑ График зависимости амплитуды тока через резистор построен как график модуля функции (6), потому что изменение знака этой функции соответствует изменению фазы колебаний этого тока.