Слободянюк А.И. Физика 10/2.3
§2. Кинематическое описание механического движения материальной точки
2.3 Ускорение при движении точки по прямой
После того, как мы разобрались с понятием мгновенной скорости («скорости в данный момент времени»), у нас появилась возможность говорить об изменении скорости, определить физическую величину, описывающую это изменение. Пусть в момент времени t0 скорость точки была υ0 , а в момент времени t1 > t0 стала равной υ1. Тогда отношение изменения скорости к промежутку времени, в течение которого это изменение произошло, называется ускорением точки
Можно сказать, что ускорение - это скорость изменения скорости тела.
Ускорение физическая величина, размерность которой есть отношение размерности скорости к размерности времени, поэтому в системе СИ размерность ускорения [a] = [υ]/[t] = (м/с)/с = м/с2 - «метр разделить на секунду в квадрате» или «метр в секунду за секунду».
Обсуждая данное определение, мы должны повторить все наши рассуждения, касающиеся перехода от понятия средней к понятию мгновенной скорости. Так возможны ситуации, когда отношение \(~\frac{\Delta \upsilon}{\Delta t}\) не зависит от величины интервала Δt - в этом случае ускорение является постоянной величиной, и такое движение называется равноускоренным. Если же величина \(~\frac{\Delta \upsilon}{\Delta t}\) зависит от промежутка времени, то формула (1) дает значение среднего ускорения на интервале времени от t0 до t1. Для более детального описания движения необходимо рассмотреть предельный переход к малому промежутку времени, тогда предельное значение отношения \(~\frac{\Delta \upsilon}{\Delta t}\) будет являться мгновенным ускорением, или ускорением «в данный момент времени».
Заметим, что ускорение, как и скорость, может быть как положительным, так и отрицательным. Напомним, что знак скорости указывает направление движения. Смысл знака ускорения иной - он показывает направление изменения скорости.
Рассмотрим теперь геометрический смысл мгновенного ускорения. Для этого построим график зависимости скорости от времени для некоторой движущейся точки (на рис. 7 - плавная кривая A0A1). Пусть в момент времени t0 скорость тела равна υ0 (точка A0 на графике), а в момент времени t0 - скорость υ1 (точка A1 на графике). В прямоугольном треугольнике A0A1C отношение длин катетов \(~\frac{|A_1C|}{|A_0C|} = \frac{\Delta \upsilon}{\Delta t}\) (то есть среднее ускорение) численно равно тангенсу угла наклона секущей A0A1 к оси времени. При уменьшении интервала времени (то есть при t1 → t0) секущая A0A1 стремится к касательной A0B. Следовательно, тангенс угла наклона касательной к графику зависимости скорости от времени численно равен мгновенному ускорению.
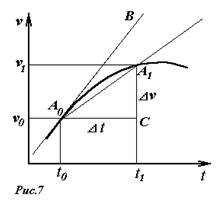
Обязательно следует отметить, что к выражению «тангенс угла наклона» (как и в случае скорости) необходимо относится с физической, а не с геометрической точки зрения - длины рассматриваемых катетов являются физическими величинами, имеющими различную размерность, поэтому и «тангенс» имеет размерность - в данном случае - ускорения. Поэтому в дальнейшем мы будем использовать термин - коэффициент наклона касательной к оси времени.
При равномерном движении с постоянной скоростью υ0 график зависимости скорости от времени является прямой линией, параллельной оси времени (на рис.8 - прямая AB). Рассмотрим промежуток времени от t0 до t1. Произведение величины этого интервала (t10 - t0) на скорость υ0 равно, с одной стороны изменению координаты Δx, а с другой площади прямоугольника под графиком зависимости скорости от времени.
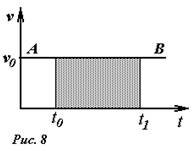
Площадь под графиком следует понимать опять же таки в физическом смысле - как произведение физических величин, имеющих различную размерность, а не в чисто геометрическом смысле - как произведение длин отрезков.
Площадь под графиком зависимости скорости от времени равна изменению координаты при любой зависимости скорости от времени υ(t). Для доказательства этого утверждения достаточно разбить время движения на малые интервалы, в течение которых движение можно считать равномерным.
Дополним наше определение площади под кривой еще одной договоренностью - будем считать, что если кривая лежит под осью времени (то есть скорость отрицательна), то и соответствующую площадь будем считать отрицательной (см. рис. 9).
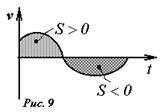
В случае произвольного движения ускорение также может изменяться в процессе движения. Таким образом, можно говорить о зависимости ускорения от времени (или от координаты) и представлять эту зависимость графически. Рассматривая график зависимости ускорения от времени, можно показать, что площадь под графиком этой зависимости численно равна изменению скорости точки (доказательство аналогично рассмотрению зависимости скорости от времени).
