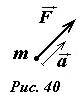Слободянюк А.И. Физика 10/4.3
§4. Основные законы динамики
4.3 Законы динамики Ньютона.
В 1723 году вышла книга английского ученого Исаака Ньютона «Математические начала натуральной философии», в которой были сформулирована система законов динамики, подобная системе аксиом геометрии Эвклида. В отличие от математических аксиом законы физики являются обобщением громадного числа физических экспериментов, также они подтверждаются справедливостью многочисленных следствий применения этих законов при описании механического движения. Тем не менее, с формальной точки зрения их можно рассматривать именно как аксиомы, не следующие из других более общих законов.
Три закона динамики И.Ньютона следует рассматривать в тесной взаимосвязи, так как только в совокупности они составляют фундамент динамики - науки, позволяющей описывать механическое движение, выяснять причины изменения скоростей тел, объяснять и управлять этим движением. Сразу подчеркнем, что знание только трех законов динамики не дает возможности решить ни одной конкретной задачи – такие возможности появляются только в том случае, когда они дополняются большим числом других законов, дающим выражения для сил конкретных взаимодействий.
Законы динамики связывают ускорения тел с характеристиками тел (массами) и их взаимодействий (силами), поэтому неудивительно, что в основу динамики И. Ньютоном были положены именно три закона.
1 закон Ньютона. В качестве 1 закона Ньютоном был взят закон инерции Г. Галилея, который был сформулирован и обоснован нами ранее: существуют инерциальные системы отсчета, т.е. такие системы отсчета, в которых тело движется равномерно и прямолинейно, если другие тела на него не действуют. Основная роль этого закона – подчеркнуть, что в этих системах отсчета все ускорения, приобретаемые телами, являются следствиями взаимодействий тел. Дальнейшее описание движения следует проводить только в инерциальных системах отсчета.
2 закон Ньютона утверждает, что причиной ускорения тела является взаимодействие тел, характеристикой которого является сила. Этот закон дает основное уравнение динамики, позволяющее, в принципе, находить закон движения тела, если известны силы, действующие на него. Этот закон может быть сформулирован следующим образом (рис. 40):
Ускорение точечного тела (материальной точки) прямо пропорционально сумме сил, действующих на тело, и обратно пропорционально массе тела
здесь \(~\vec F\) - результирующая сила, то есть векторная сумма всех сил, действующих на тело.
На первый взгляд, уравнение (1) является другой формой записи определения силы, данного в предыдущем разделе. Однако, это не совсем так. Во-первых, закон Ньютона утверждает, что в уравнение (1) входит сумма всех сил, действующих на тело, чего нет в определении силы. Во-вторых, 2 закон Ньютона однозначно подчеркивает, что сила является причиной ускорения тела, а не наоборот.
Наконец, все физические величины определяются на основании частных случаев тех или иных физических законов, так что 2 закон Ньютона не является в этом случае исключением. С одной стороны, этот закон позволяет изучать различные виды взаимодействий, т.е. экспериментально получать законы этих взаимодействий. С другой стороны, при известных силах, этот закон дает уравнение, позволяющее находить закон движения тела.
Так же подчеркнем, что первый закон не является следствием второго. Формально, если сумма сил, действующих на тело равна нулю, то ускорение тела равно нулю, то есть тело движется равномерно и прямолинейно. Однако, напомним, что именно первый закон указывает те системы отсчета, в которых выполняется второй закон.
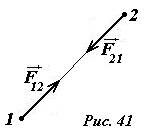
3 закон Ньютона подчеркивает, что причиной ускорения является взаимное действие тел друг на друга. Поэтому силы, действующие на взаимодействующие тела, являются характеристиками одно и того же взаимодействия. С этой точки зрения нет ничего удивительного в третьем законе Ньютона (рис. 41):
точечные тела (материальные точки) взаимодействуют с силами равными по величине и противоположными по направлению и направленными вдоль прямой, соединяющей эти тела:
где \(~\vec F_{12}\) - сила, действующая на первое тело, со стороны второго, а \(~\vec F_{21}\) - сила, действующая на второе тело, со стороны первого.
Очевидно, что эти силы имеют одинаковую природу. Этот закон также является обобщением многочисленных экспериментальных фактов. Обратим внимание, что фактически именно этот закон является основой определения массы тел, данного в предыдущем разделе.
Сформулированные законы динамики играют роль своеобразных аксиом, то есть утверждений, не выводимых из более общих физических законов. Обратите внимание, что рассматриваемые законы сформулированы для точечных тел (материальных точек). Их применение для реальных тел, имеющих конечные размеры, требует уточнения и обоснования.
Смотреть HD
видео онлайн
бесплатно 2022 года