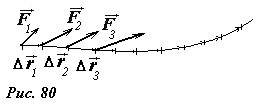Слободянюк А.И. Физика 10/6.3
§6. Законы сохранения в механике
6.3 Работа. Кинетическая энергия.
Продолжим наш разговор о результате действия силы. Во-первых, сила есть причина ускорения (то есть изменения скорости) тела, во-вторых, если сила действует на систему в течение некоторого промежутка времени, то результатом этого действия является изменение импульса системы. Сейчас мы рассмотрим результат действия силы на некотором пространственном интервале пути.
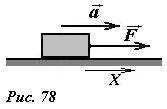
Рассмотрим простейшую ситуацию, когда тело (материальная точка) движется вдоль прямой под действием постоянной силы F, направленной вдоль той же прямой (рис. 78). В этом случае ускорение тела остается постоянным и определяется вторым законом Ньютона \(~\vec a = \frac{\vec F}{m}\) . Пусть тело сместилось на расстояние Δx, которое может быть выражено по кинематической формуле \(~\Delta x = \frac{\upsilon^2 - \upsilon^2_0}{2a}\) . Объединяя эти две приведенные формулы, получим следующее выражение
Итак, мы видим, что произведение силы на интервал времени ее действия равно изменению импульса тела, то произведение силы на смещение тела равно изменению такой характеристики движения [1] как \(~K = \frac{m \upsilon^2}{2}\) , которая, как вы знаете, называется кинетической энергией тела.
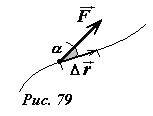
Обсудим теперь общую ситуацию – тело движется по произвольной траектории, результирующая внешняя сила не является постоянной, может изменяться как по величине, так и по направлению. Обозначим перемещение тела за малый промежуток времени \(~\Delta \vec r\) (рис. 79). Действующую силу (и ускорение) имеет смысл разложить на две составляющих: тангенциальную F cos α, параллельную вектору перемещения, и нормальную, перпендикулярную вектору перемещения F sin α. Как ранее было показано, нормальное ускорение (и его причина сила) не изменяют модуля скорости (изменяется только ее направление). Таким образом, изменение модуля скорости полностью определяется тангенциальной составляющей силы. На малом интервале времени траекторию движения можно приближенно считать отрезком прямой линии, поэтому для него применима формула (1). Поэтому, изменение кинетической энергии тела на малом интервале траектории равно произведению тангенциальной составляющей силы на модуль перемещения
Правую часть этого выражения можно компактно записать в виде скалярного произведения векторов силы и перемещения \(~F \cos \alpha \cdot \Delta r = \vec F \cdot \Delta \vec r\) . Эта физическая величина играет чрезвычайно важную роль в физике, поэтому не случайно она получила «персональное» название – «механическая работа» - \(~A = \vec F \cdot \Delta \vec r\) . Также не случайно, что имеются специальные единицы измерения работы (и энергии): так в системе СИ единицей измерения работы является Джоуль – работа, которую совершает сила в 1 ньютон при перемещении тела на 1 метр в направлении действия силы. Работа есть характеристика действия силы: если под действием силы произошло перемещение тела, то говорят, что сила совершила работу [2]. В результате совершенной работы происходит изменение кинетической энергии тела.
Результат, полученный для малого перемещения, можно распространить на любой участок траектории. Для этого достаточно разбить траекторию на малые участки (рис. 80) и просуммировать как произведенную работу, так и изменение кинетической энергии.
Таким образом, мы доказали теорему о кинетической энергии тела: изменение кинетической энергии тела равно работе внешних сил.
В простейшем случае движения тела вдоль прямой и при постоянной силе работа равна произведению вектора силы на вектор перемещения \(~A = \vec F \cdot \Delta \vec S = F S \cos \alpha\) , где α - угол между указанными векторами. Как следует из определения, работа может быть как положительной, если угол α острый (в этом случае кинетическая энергия тела возрастает), так и отрицательной, если угол α - тупой (в этом случае кинетическая энергия уменьшается). Если сила не является постоянной, вычисление работы этой силы требует особых приемов.
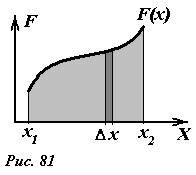
Пусть на тело, движущееся вдоль оси X, действует внешняя сила, модуль которой зависит от координаты тела. Построим график (рис. 81) зависимости модуля этой силы от координаты F(x). При смещении тела на малую величину Δx можно пренебречь изменением величины силы на этом малом интервале. Тогда работа, совершенная на этом участке, может быть вычислена по формуле δA = F(x)Δx. Легко заметить, что численно она равна площади «полоски», основанием которой является Δx, а высотой F(x). Для произвольного интервала изменения координаты тела от x1 до x2 , суммарная работа, совершенная переменной силой, будет численно равна площади криволинейной трапеции под графиком функции F(x) .
Обсудим теперь результат действия внешних сил не на отдельное взятое тело (материальную точку), а на систему взаимодействующих тел. В этом случае результат действия внешних сил может проявляться не только в изменении кинетической энергии системы, но и приводить к другим последствиям: изменению взаимного расположения тел системы (например, деформации тела), изменению температуры системы, появлению звука, света, электрических зарядов и так далее. Иными словами, результат воздействия внешних сил зависит от внутренних свойств рассматриваемой системы, в частности от характера внутренних сил системы. Однако оказывается возможным установить чрезвычайно общие закономерности поведения систем, введя для них специальную характеристику – энергию, частным случаем которой является кинетическая энергия.
Дать общее определение энергии системы чрезвычайно затруднительно (да и вряд ли возможно) – эта физическая величина фигурирует во всех разделах физики, принимает множество различных форм, с которыми вы будете знакомиться на протяжении всего изучения физики. Общим для всех этих форм является то, что различные формы энергии могут переходить друг в друга в ходе многообразных физических процессов, при этом оставаясь постоянной для замкнутых систем. Своеобразным образом энергия является некоторой универсальной мерой различных форм движения [3], а сохранение энергии свидетельствует о неуничтожимости движения.
В механике под энергией понимают способность системы совершить механическую работу. Если рассматриваемая система совершает положительную работу над внешними телами, то энергия системы уменьшается на величину совершенной работы; если внешние силы совершают положительную работу над системой, то энергия системы возрастает на величину совершенной работы. Таким образом, энергия и работа являются близкими взаимосвязанными, но не идентичными понятиями. Так работа является характеристикой физических процессов, а энергия - характеристика состояния системы, причем работа играет роль меры изменения энергии системы.
При изучении различных видов энергии мы будем рассматривать два подхода: первый - внешние силы совершают работу над системой, второй – система совершает работу над внешними телами. В обоих случаях изменение энергии равно совершенной работе, что позволяет получать математические выражения для различных форм энергии.
Подойдем с этой точки зрения к понятию кинетической энергии. Мы показали, что работа внешних сил, совершенная над телом, приводит к увеличению его кинетической энергии, которая выражается формулой
Сейчас покажем, что движущееся тело способно совершить работу, которая в точности определяется формулой (2).
Итак, пусть тело массой m, движется со скоростью V0. Для торможения тела до полной остановки к нему необходимо приложить некоторую силу \(~\vec F\), направленную в сторону, противоположную его скорости.
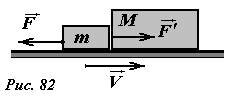
Для определенности будем считать, что рассматриваемое тело взаимодействует с другим телом M, причем природа сил взаимодействия может быть любой (рис. 82). По третьему закону Ньютона, движущееся тело действует на тормозящее тело с силой \(~\vec F\,'\) , равной по величине и противоположной по направлению силе \(~\vec F\) . Следовательно, тело m посредством этой силы будет совершать работу над телом M. Считая для простоты, что силы взаимодействия постоянны по величине, можем записать, что смещение S движущегося тела до остановки определяется кинематической формулой (т.к. конечная скорость равна нулю)
где \(~a = \frac{F}{m}\) - модуль ускорения движущегося тела. С учетом этих соотношений, работа, совершенная силой \(~\vec F\,'\) (движущимся телом), рассчитывается следующим образом:
что в точности равно начальной кинетической энергии тела.
Примечания
- ↑ В течение более сотни лет среди ученых-физиков шла бурная дискуссия, что является «мерой движения»: импульс \(~m \vec \upsilon\) , или кинетическая энергия \(~\frac{m \upsilon^2}{2}\) , которую называли «живой силой».
- ↑ Мы знаем, что сила есть характеристика взаимодействия тел, поэтому можно говорить о работе, совершенной одним телом над другим. Выражения «сила совершила работу», «тело совершило работу» можно рассматривать как эквивалентные. Также аналогичными являются выражения «внешняя сила совершила работу» и «над телом совершена работа».
- ↑ В данном случае мы имеем в виду не только механическое движение, а движение в философском смысле – «всякое изменение вообще».
Смотреть HD
видео онлайн
бесплатно 2022 года