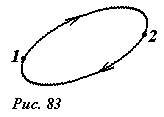Слободянюк А.И. Физика 10/6.4

Содержание книги

Предыдующая страница

§6. Законы сохранения в механике

6.4 Потенциальная энергия.

Если тела взаимодействуют между собой, то есть если между ними действуют силы, то в процессе их взаимного движения также может совершаться механическая работа. Следовательно, можно говорить, что взаимодействующие тела обладают энергией. Энергия, обусловленная взаимодействием тел, их взаимным расположением, называется потенциальной. Если сила взаимодействия совершает положительную работу, то потенциальная энергия этого взаимодействия уменьшается на величину совершенной работы.

Как мы покажем в дальнейшем, многие взаимодействия обладают важнейшим свойством: работа этих сил не зависит от формы траектории движения, а полностью определяется начальным и конечным положением тела. Силы, которые удовлетворяют этому условию, называются потенциальными, или консервативными . При изучении энергетических характеристик различных взаимодействий вопрос о зависимости (или независимости) работы от формы траектории является важнейшим, поэтому при изучении взаимодействий мы всегда будем его анализировать. Если взаимодействия удовлетворяет условию потенциальности, то можно ввести специальную функцию от координат всех взаимодействующих тел, описывающую взаимодействие – потенциальную энергию U. Строго говоря, эта функция от взаимного расположения всех взаимодействующих тел. Однако во многих случаях можно рассматривать движение одного тела, при условии, что остальные тела неподвижны, тогда можно говорить о потенциальной энергии отдельного тела и рассматривать потенциальную энергию как функцию координат только этого движущегося тела U(x,y,z). Эта функция имеет следующий физический смысл: работа потенциальной силы при перемещении тела из одной точки с координатами (x₁,y₁,z₁) в другую, с координатами (x₂,y₂,z₂) равна изменению потенциальной энергии, взятому с противоположным знаком:

\(~A = -\Delta U = -(U(x_2,y_2,z_2) - U(x_1,y_1,z_1))\) . (1)

Изменение знака в данном определении достаточно логично: если сила совершила положительную работу (A > 0), то ее энергия уменьшается (ΔU < 0).

Условие потенциальности взаимодействия может быть сформулировано в эквивалентном виде: работа потенциальной силы по любой замкнутой траектории равна нулю. Доказательство этого утверждения непосредственно следует из определения потенциальной энергии.

Действительно, пусть некоторое тело переместилось по некоторой замкнутой траектории (рис. 83). Тогда при движении от точки 1 до точки 2, работа силы определяется формулой (1) A₁₂ = -(U₂ - U₁), а при движении в обратном направлении по любой другой траектории, работа будет равна A₂₁ = -(U₁ - U₂). Суммарная же работа будет равна нулю.

Заметьте, что в том случае, когда работа силы зависит от траектории движения, нельзя определить функцию потенциальной энергии, так как работа зависит не только от начального и конечного положения тела.

Мы можем установить связь между силой и потенциальной энергией взаимодействия. Пусть под действием силы \(~\vec F\) тело сместилось на малое расстояние Δx вдоль оси X, при этом совершена работа A = F_xΔx (где F_x - проекция силы на ось X). Уменьшение потенциальной энергии равно совершенной работе, поэтому

\(~\Delta U = -A = -F_x \Delta x\) . (2)

Из этой формулы также следует выражение, позволяющее определить силу по известной потенциальной энергии взаимодействия

\(~F_x = -\frac{\Delta U}{\Delta x}\) . (3)

Аналогичным образом определяются проекции силы на другие оси координат.

Обратим внимание на еще одно общее обстоятельство, общее для различных видов потенциальной энергии. Как следует из определения, физический смысл имеет изменение потенциальной энергии, так как только изменение энергии определяет экспериментально измеряемые величины – работу и силу. Следовательно, если к функции потенциальной энергии U(x,y,z) во всех точках добавить постоянное слагаемое, то эта добавка никак не скажется на поведении системы. Поэтому часто говорят, что потенциальная энергия определяется с точностью до произвольного слагаемого, или нулевой уровень потенциальной энергии выбирается произвольно.

Теперь мы можем дать еще одно толкование потенциальной энергии.

Потенциальная энергия тела U(x,y,z), находящегося в точке с координатами (x,y,z) равна работе, которую совершают силы взаимодействия при перемещении тела из данной точки, в точку с координатами (x₀,y₀,z₀), где потенциальная энергия принимается равной нулю U(x₀,y₀,z₀) = 0.

Таким образом, потенциальная энергия в некоторой точке определяется силами взаимодействия не только в данной точке, но и на всем пути до точки с нулевой потенциальной энергией.

С другой стороны, если над системой внешние силы совершают работу, то энергия системы увеличивается, причем изменение энергии системы равно совершенной работе. Однако работа внешних сил может пойти на увеличение любого вида энергии системы – кинетической, потенциальной и других.

Итак, для расчета потенциальной энергии необходимо доказать, что работа силы не зависит от траектории движения, а затем подсчитать эту работу, которая и будет равна изменению потенциальной энергии.

Примечания

Следующая страница