А. Длина волны

Длина волны. Связь длины волны со скоростью ее распространения. Уравнение волны

Как уже отмечалось, возмущение, создаваемое колеблющимся в упругой среде телом, передается от одной точки среды к другой. Это происходит не мгновенно, а с определенной скоростью. Скоростью распространения волны называется физическая величина, определяемая расстоянием, которое проходит любая точка фронта волны за единицу времени. Вектор скорости \(\vec \upsilon\) направлен по нормали к волновой поверхности в сторону распространения волны и в однородной изотропной среде совпадает с направлением луча. Следует отличать скорость распространения волны от скорости колебания частиц среды около своих положений равновесия.

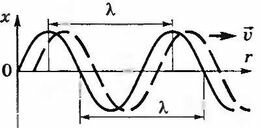
Пусть волна распространяется вдоль горизонтальной оси (например, вдоль упругого горизонтального шнура). В данный момент времени форма волны повторяется в пространстве вдоль шнура через определенные отрезки. На рисунке 15.7 показан профиль волны в определенный момент времени. С течением времени вся эта картина перемещается со скоростью \(\upsilon\) слева направо (штриховая линия).

Рис. 15.7

Расстояние между ближайшими точками, колеблющимися в одинаковых фазах (рис. 15.7), называется длиной волны. Длина волны \(~\lambda\) равна расстоянию, на которое распространяется фронт волны за время, равное периоду \(~T\) колебаний источника волн\[~\lambda = \upsilon T.\]

Так как \(T = \frac{1}{\nu};\) \(\nu = \frac{\omega}{2 \pi},\) то скорость волны связана с частотой колебаний уравнением \(~\upsilon = \lambda \nu.\) Отсюда \(\lambda = \frac{\upsilon}{\nu} = \frac{2 \pi \upsilon}{\omega},\) где \(~\omega\) — циклическая частота колебаний, \(~\nu\) и \(~\omega\) зависят только от свойств источника волны.

При возникновении волн в среде их частота определяется частотой колебаний источника, а скорость распространения волны зависит от свойств среды. Поэтому волны одной и той же частоты имеют различную длину в разных средах.

Выведем уравнение плоской волны.

Пусть источник совершает гармонические колебания по закону

\(~x = A \sin \omega t,\)

где х — смещение, А — амплитуда, \(~\omega\) — циклическая частота, t — время.

В точках, отстоящих на расстоянии r от источника, колебания частиц среды волнового фронта будут также гармоническими, с той же частотой, но будут отставать во времени от колебаний источника на \(\Delta t = \frac{r}{\upsilon}.\)

Тогда смещение точки среды с координатой r в момент времени t

\(x = A \sin \omega \Bigr( t-\frac{r}{\upsilon} \Bigl),\) или \(x = A \sin \Bigr( \omega t-\frac{\omega r}{\upsilon} \Bigl).\)

Это и есть уравнение плоской бегущей монохроматической волны (при этом предполагают, что затуханием волны в процессе ее распространения можно пренебречь). Смещение любой точки среды из равновесного положения при прохождении волны является функцией двух переменных: времени t и расстояния r до равновесного положения точки среды.

Из уравнения волны следует:

1. Амплитуда плоской незатухающей волны в данной точке среды постоянна и равна амплитуде колебаний источника.

2. Любая точка среды совершает гармонические колебания, начальная фаза которых зависит от удаления r данной точки от источника колебаний:

\(~x = A \sin(\omega t + \alpha),\) где \(\alpha = -\frac{\omega r}{\upsilon}.\)

3. Положения колеблющихся точек среды в некоторый фиксированный момент времени описываются уравнением

\(x = A \sin \Bigr( \frac{\omega r}{\upsilon} + \beta \Bigl),\) где \(~\beta = -\omega t\)

имеет разное значение в разные моменты времени.

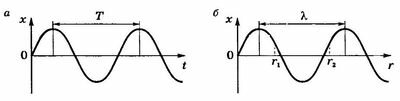
На рисунке 15.8, б приведен график этой функции при t = 0, представляющий собой "моментальный снимок" волны, т.е. положение всех частиц среды, в которой распространяется волна, в момент времени t = 0 — график волны. В отличие от графика колебаний (рис. 15.8, а), который показывает зависимость смещения одной частицы от времени в данной точке среды, график волны (рис. 15.8, б) показывает зависимость смещения всех частиц среды из положения равновесия от расстояния г до источника колебаний в некоторый фиксированный момент времени.

Рис. 15.8

Найдем разность фаз колебаний двух точек среды, находящихся на расстоянии \(~\Delta r = r_2 - r_1\) друг от друга (рис. 15.8, б). Колебания этих точек описываются уравнениями:

\(x_1 = A \sin \omega \Bigr( t - \frac{r_1}{\upsilon} \Bigl);\) \(x_2 = A \sin \omega \Bigr( t - \frac{r_2}{\upsilon} \Bigl).\)

Разность фаз \(\Delta \varphi_1 = \varphi_1 - \varphi_2\) будет равна

\(\Delta \varphi = \omega \Bigr( t - \frac{r_1}{\upsilon} \Bigl) - \omega \Bigr( t - \frac{r_2}{\upsilon} \Bigl) = \frac{\omega}{\upsilon}(r_2-r_1) = \frac{2 \pi}{T \upsilon}(r_2 - r_1) = \frac{2 \pi}{\lambda} \Delta r.\)

Если две точки находятся на расстоянии \(~\Delta r = \lambda,\) то разность фаз колебаний этих точек \(\Delta \varphi = 2 \pi,\) что соответствует данному выше определению длины волны.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — С. 428-430.