Решение. Графики. B11

Условие

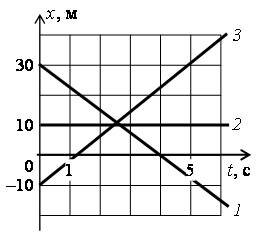
B11. По графикам зависимости координаты тел от времени (рис. 1) определите для каждого тела:

а) начальную координату;

б) координату через 4 с;

в) проекцию скорости;

г) уравнение координаты (уравнение движения);

д) когда координата будет равна 20 м?

Рис. 1

Решение

а) Определите для каждого тела начальную координату.

Графический способ. По графику находим значения координат точек пересечения графиков с осью 0х (на рис. 2 а эти точки выделены):

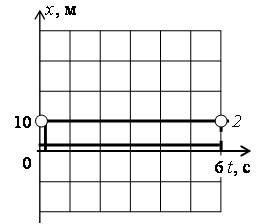
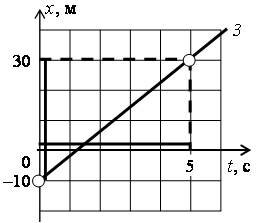
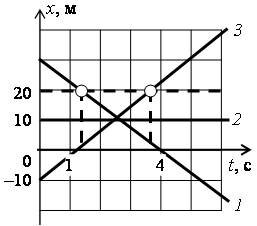
x₀₁ = 30 м; x₀₂ = 10 м; x₀₃ = –10 м.

Рис. 2 а

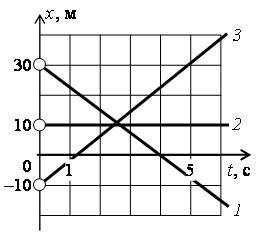
б) Определите для каждого тела координату через 4 с.

Графический способ. По графику находим значения координат точек пересечения графиков с перпендикуляром, проведенным к оси 0t в точке t = 4 с (на рис. 2 б эти точки выделены): x₁(4 с) = 0; x₂(4 с) = 10 м; x₃(4 с) ≈ 20 м.

Аналитический способ. Составьте уравнение движения и по нему определить значение координаты при t = 4 с (см. пункт г).

Рис. 2 б

в) Определите для каждого тела проекцию скорости.

Графический способ. Проекция скорости \(~\upsilon_x = \tan \alpha = \frac{\Delta x}{\Delta t} = \frac{x_2 - x_1}{t_2-t_1}\) , где α – угол наклона графика к оси 0t; Δt = t₂ – t₁ – произвольный промежуток времени; Δυ = υ₂ – υ₁ – промежуток скоростей, соответствующий промежутку времени Δt = t₂ – t₁.

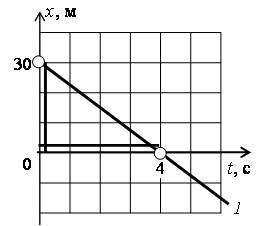
Для графика 1: пусть t₂ = 4 с, t₁ = 0, тогда x₂ = 0, x₁ = 30 м и υ_1x = (0 - 30 м)/(4 с - 0) = –7,5 м/с (рис. 3 а).

Рис. 3 а

Для графика 2: пусть t₂ = 6 с, t₁ = 0, тогда x₂ = 10 м, x₁ = 10 м и υ_2x = (10 м - 10 м)/(6 с - 0) = 0 (рис. 3 б).

Рис. 3 б

Для графика 3: пусть t₂ = 5 с, t₁ = 0, тогда x₂ = 30 м, x₁ = –10 м и υ_3x = (30 - (-10 м))/(5 с - 0) = 8 м/с (рис. 3 в).

Рис. 3 в

Аналитический способ. Запишем уравнение координаты при равномерном прямолинейном движении в общем виде x = x₀ + υ_x·t. Используя значения начальной координаты (см. пункт а) и координаты при t = 4 с (см. пункт б), найдем значение проекции скорости\[~\upsilon_x = \frac{x - x_0}{t}\] .

г) Определите для каждого тела уравнение координаты.

Уравнение координаты при равномерном прямолинейном движении в общем виде 'x = x₀ + υ_x·t.

Для графика 1: т.к. x₀₁ = 30 м, υ_1x = –7,5 м/с, то x₁ = 30 – 7,5t. Проверим пункт б: x₁(4 с) = 30 – 7,5·4 = 0, что соответствует ответу.

Для графика 2: т.к. x₀₂ = 10 м, υ_2x = 0, то x₂ = 10. Проверим пункт б: x₂(4 с) = 10 (м), что соответствует ответу.

Для графика 3: т.к. x₀₃ = –10 м, υ_3x = 8 м/с, то x₃ = –10 + 8t. Проверим пункт б: x₃(4 с) = –10 + 8·4 = 22 (м), что соответствует приблизительно ответу.

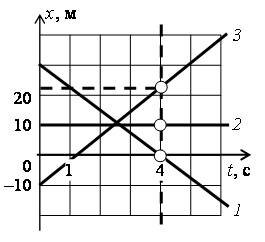
д) Определите, когда координата тела будет равна 20 м?

Графический способ. По графику находим значения времени точек пересечения графиков с перпендикуляром, проведенном к оси 0x в точке x = 20 м (на рис. 4 эти точки выделены): t₁(20 м) ≈ 1,5 с; t₃(20 м) ≈ 3,5 с.

График 2 параллелен перпендикуляру, следовательно, координата тела 2 никогда не будет равной 20 м.

Рис. 4

Аналитический способ. Записать уравнение координаты для каждого тела и найти при каком значении времени t, координата станет равной 20 м.