Решение. Масса. Сила. Второй закон Ньютона. B20

Условие

B20. Снаряд массой 10 кг вылетает из ствола орудия со скоростью 600 м/с. Определите среднюю силу давления пороховых газов на снаряд, если длина ствола орудия 3 м, а движение снаряда равноускоренное.

Решение

снаряд;

действие сил;

равноускоренное движение;

m = 10 кг;

l = 3 м;

υ = 600 м/с;

F – ?

По условию снаряд движется прямолинейно равноускоренно. Скорость вылета снаряда из ствола – это конечная скорость, начальная скорость υ₀ = 0. Для снаряда длина орудия – это перемещение снаряда, т.е. Δr = l.

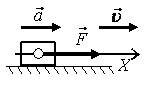
Направим ось 0Х вдоль скорости. Ускорение направлено в сторону движения и в сторону равнодействующей силы (рис. 1). Зная перемещение, начальную и конечную скорости, можно найти ускорение \(~\Delta r_x = \frac{\upsilon^2_x - \upsilon^2_{0x}}{2a_x}\) , где Δr_x = Δr = l, υ_x = υ, υ₀ = 0. Ускорение и сила связаны соотношением F_x = m∙a_x, где F_x = F, a_x = a. Тогда

\(~a = \frac{\upsilon^2}{2l} ; F = m \cdot \frac{\upsilon^2}{2l}\) ; F = 6∙10⁵ Н.

Рис. 1