Решение. Относительность движения. B14
Условие
B14. По двум параллельным железнодорожным линиям равномерно движутся два поезда: грузовой длиной 630 м со скоростью 48 км/ч и пассажирский длиной 120 м со скоростью 102 км/ч. В течение какого времени пассажирский поезд проходит мимо машиниста грузового, если поезда движутся:
а) в одном направлении;
б) навстречу друг другу?
Решение
По условию наблюдение ведется из грузового поезда, поэтому υc = υgruz = 48 км/ч ≈ 13,3 м/с. Тогда υton = υpass = 102 км/ч ≈ 28,3 м/с, а длина пассажирского поезда – это перемещение, которое нужно совершить относительно грузового (подвижной системы), т.е. Δrtop = lpass = 120 м. Время найдем по формуле \(~t = \frac{\Delta r_{topx}}{\upsilon_{topx}}\) (т.к. известно Δrtop), где υtop – скорость пассажирского поезда относительно грузового. Найдем эту скорость.
Запишем закон сложения скоростей в векторном виде \(~\vec \upsilon_{ton} = \vec \upsilon_c + \vec \upsilon_{top} ; \vec \upsilon_{top} = \vec \upsilon_{ton} - \vec \upsilon_c = \vec \upsilon_{pass} - \vec \upsilon_{gruz}\) и в проекции на ось 0X:
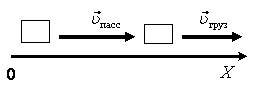
а) υtop x = υpass – υgruz (рис. 1 а). Так как υtop x > 0, то Δrtop x > 0; \(~t = \frac{\Delta r_{top}}{\upsilon_{pass} - \upsilon_{gruz}} = \frac{l_{pass}}{\upsilon_{pass} - \upsilon_{gruz}}\) ; t ≈ 8,0 с.
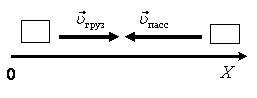
б) υtop x = –υpass – υgruz (рис. 1 б). Так как υtop x < 0, то Δrtop x < 0; \(~t = \frac{-\Delta r_{top}}{-\upsilon_{pass} - \upsilon_{gruz}} = \frac{l_{pass}}{\upsilon_{pass} + \upsilon_{gruz}}\) ; t ≈ 2,9 с.