Решение. Сила упругости. B15
Материал из PhysBook
Условие
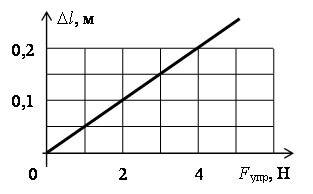
B15. По графику зависимости изменения длины резинового жгута от приложенной к нему силы найдите жесткость жгута (рис. 1).
Решение
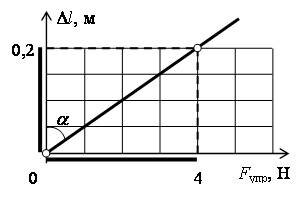
При деформации сила упругости и коэффициент жесткости тела связаны соотношением Fупр = k∙Δl. Так как это линейная функция, то \(~k = \operatorname{tg} \alpha\), α – угол наклона графика функции Fупр = f(Δl) к оси абсцисс или функции Δl = f(Fупр) к оси ординат. Тогда
\(~k = \operatorname{tg} \alpha = \frac{\Delta F}{\Delta(\Delta l)} = \frac{F_2 - F_1}{\Delta l_2 - \Delta l_1}\) .
Из графика выбираем любые значения Δl1 и Δl2 и соответствующие им значения F1 и F2.
Для Δl1 = 0, F1 = 0, для Δl2 = 0,2 м, F2 = 4 Н (рис. 2). В итоге получаем k = (4 Н - 0) / (0,2 м - 0) = 20 Н/м.