Решение. Сила упругости. B19

Условие

B19. Два мальчика растягивают резиновый жгут, прикрепив к его концам динамометры. Когда жгут удлинился на 2 см, динамометры показывали силы по 20 Н каждый. Что показывают динамометры при растяжении жгута на 6 см?

Решение

Два динамометра, жгут; деформация;

Δl1 = 2 см = 2∙10-2 м;

F1 = 20 Н;

Δl2 = 6 см = 6∙10-2 м;

F2 – ?

При деформации сила упругости и удлинение тела связаны соотношением F_упр = k∙Δl, где F_упр = F – показание динамометра.

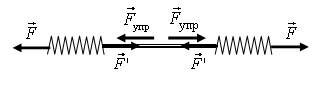
• Докажем это: рассмотрим одну из пружин динамометра, например, левую (рис. 1). Показание динамометра равно силе упругости, действующей в пружине (\(~\vec F\)) . Так как динамометр неподвижен (по умолчанию), то с такой же силой на пружину действует и жгут (\(~\vec F'\)) , т.е. F = F’. По третьему закону Ньютона, сила, с которой динамометр действует на жгут, равна силе, с которой жгут действует на динамометр, т.е. F’ = F_упр. Следовательно, F_упр = F. Аналогично можно провести доказательство и для правого динамометра, причем, т.к. жгут неподвижен, то F_{упр пр} = F_{упр лев}.

Рис. 1

Тогда F = k∙Δl (1). Для первого динамометра уравнение (1) примет вид F₁ = k₁∙Δl₁, для второго – F₂ = k₂∙Δl₂, где k₁ = k₂, т.к. жгут один и тот же. В итоге получаем\[~\frac{F_2}{F_1} = \frac{\Delta l_2}{\Delta l_1} ; F_2 = F_1 \cdot \frac{\Delta l_2}{\Delta l_1}\] ; F₂ = 60 Н.